《2025年通城学典课时作业本九年级数学全一册浙教版》

9. 一个三角形三边的长度之比为$3:5:7$,与它相似的一个三角形的最长边的长度是21 cm,则其另外两边的长度之和是(D)
A.15 cm
B.18 cm
C.21 cm
D.24 cm

答案： D

10. (2024·杭州西湖期末)已知在$\triangle ABC$中,$AB= 6$,$AC= 9$,$D$,$E分别是AB$,$AC$边上的点,且$AD= 2$. 若$\triangle ABC和\triangle ADE$相似,则$AE$的长为(D)
A.5
B.3
C.$\frac{4}{3}$
D.3或$\frac{4}{3}$

答案： D

11. 如图,$\triangle ABC\backsim\triangle ADE$,$\angle E= 90^\circ$,$AC= 3$,$BC= 4$,$AE= 2$,则$AD= $$\frac{10}{3}$.

答案： $\frac{10}{3}$

12. 如图,$\triangle ABC\backsim\triangle ACD$. 若$\angle A= 35^\circ$,$\angle B= 65^\circ$,则$\angle BCD$的度数为15°.

答案： 15° 解析：
∵△ABC∽△ACD，
∴∠ACB=∠ADC，∠ACD=∠B=65°.
∴∠ADC=180°-∠A-∠ACD=180°-35°-65°=80°.
∴∠ACB=80°.
∴∠BCD=∠ACB-∠ACD=80°-65°=15°.

13. (教材P128例1变式)如图,$DE是\triangle ABC$的中位线,延长$DE至点F$,使$EF= DE$,连结$CF$. 求证：$\triangle CFE\backsim\triangle ABC$.

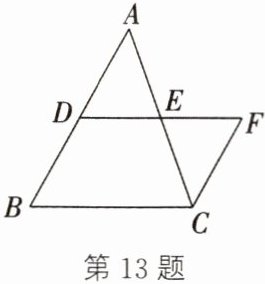
答案：
∵DE是△ABC的中位线，
∴AD=BD，AE=CE，DE//BC，DE=$\frac{1}{2}$BC.
∴△ADE与△ABC三个内角对应相等，三边对应成比例，且对应边的比为1:2.在△ADE和△CFE中，$\left\{\begin{array}{l} AE=CE,\\ ∠AED=∠CEF,\\ DE=FE,\end{array}\right.$
∴△ADE≌△CFE.
∴△CFE与△ABC三个内角对应相等，三边对应成比例，且对应边的比为1:2.
∴△CFE∽△ABC

14. (方程思想)如图,在$\triangle ABC$中,$\angle B= 90^\circ$,$AB= 5\ \text{cm}$,$BC= 7\ \text{cm}$,点$P从点A$出发,沿$AB向点B$以1 cm/s的速度运动,同时点$Q从点B$出发,沿$BC向点C$以2 cm/s的速度运动,当$P$,$Q$两点中有一点到达终点时,则同时停止运动. 设点$P运动的时间为x\ \text{s}(x＞0)$.
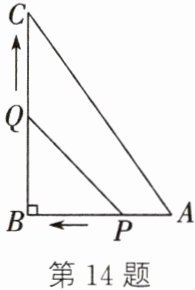
(1)点$P$运动几秒后,$\triangle PBQ的面积等于4\ \text{cm}^2$？
(2)点$P$运动几秒后,$PQ$的长为5 cm？
(3)点$P$运动几秒后,以$B$,$P$,$Q为顶点的三角形与\triangle ABC$相似？

答案： 由题意，得AP=x cm，BP=(5-x)cm，BQ=2x cm(0＜x≤3.5).（1）根据△PBQ的面积为4 cm²，可得$\frac{1}{2}$(5-x)×2x=4，整理，得x²-5x+4=0，解得x=1或x=4(舍去).
∴点P运动1 s后，△PBQ的面积为4 cm² （2）
∵∠B=90°，
∴BP²+BQ²=PQ²，即(5-x)²+(2x)²=5²，整理，得x²-2x=0，解得x=0(舍去)或x=2.
∴点P运动2 s后，PQ的长为5 cm （3）当△BQP∽△BCA时，$\frac{BQ}{BC}=\frac{BP}{BA}$，即$\frac{2x}{7}=\frac{5-x}{5}$，解得x=$\frac{35}{17}$；当△BQP∽△BAC时，$\frac{BQ}{BA}=\frac{BP}{BC}$，即$\frac{2x}{5}=\frac{5-x}{7}$，解得x=$\frac{25}{19}$.
∴x=$\frac{35}{17}$或$\frac{25}{19}$.
∴点P运动$\frac{35}{17}$s或$\frac{25}{19}$s后，以B，P，Q为顶点的三角形与△ABC相似