《2025年通城学典课时作业本九年级数学全一册浙教版》

7.(2024·宁波北仑期中)在Rt△ABC中,∠ACB= 90°,AC= 6,AB= 10,以点C为圆心,BC为半径作⊙C,则点A与⊙C的位置关系是(A)
A.点A在⊙C内
B.点A在⊙C上
C.点A在⊙C外
D.无法确定

答案： A

8. 如图,在网格(每个小正方形的边长均为1)中选取9个格点(网格线的交点称为格点).若以点A为圆心,r为半径画圆,选取的格点中,除点A外恰好有3个在圆内,则r的取值范围是(B)
A.2√2＜r＜√17
B.√17＜r≤3√2
C.√17＜r＜5
D.5＜r＜√29

答案： B

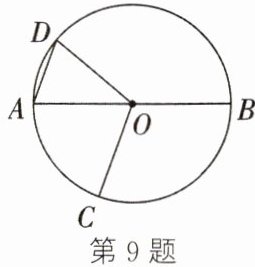
9. 如图,AB是⊙O的直径,点C,D在⊙O上,且点C,D在AB的异侧,连结AD,OD,OC.若∠AOC= 70°,且AD//OC,则∠AOD的度数为______40°.

答案： 40°

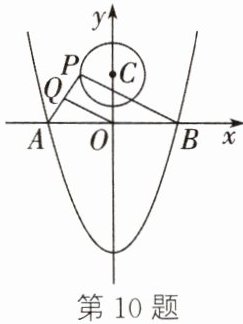
10.(2024·温州文成段考)如图,抛物线$y= 1/2x^2-8$与x轴交于A,B两点,P是以点C(0,3)为圆心,2为半径的圆上的动点,Q是线段PA的中点,连结OQ,则线段OQ长的最大值是______3.5.

答案： 3.5

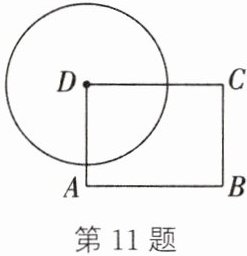
11. 如图,在矩形ABCD中,AB= 4,AD= 3,以顶点D为圆心,r为半径作圆.
(1)若A,B,C三点中有且只有一点在圆内,求r的取值范围；
(2)若A,B,C三点中至少有一点在圆内,至少有一点在圆外,求r的取值范围.

答案： 连结BD.
∵ 四边形ABCD是矩形,
∴ AB=CD,∠A=90°.又
∵ AB=4,AD=3,
∴ CD=4,BD=√(3²+4²)=5.
∴ AD＜CD＜BD.
(1)由题意,得只能是点A在圆内,点B,C均不在圆内,
∴ AD＜r≤CD,即3＜r≤4
(2)由题意,得点A一定在圆内,点B一定在圆外,
∴ AD＜r＜BD,即3＜r＜5

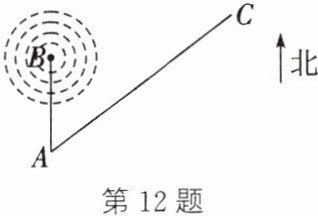
12. 如图,在A城的正北方向50 km的B处有一无线电信号发射塔,该发射塔发射的无线电信号的有效半径为100 km,AC是一条直达C城的公路.已知从A城发往C城的班车的速度为60 km/h.
(1)当班车载A城出发开往C城时,某乘客立即打开无线接收设备,班车行驶了0.5 h时,接收信号最强.此时班车到发射塔的距离是多少千米(离发射塔越近,信号越强)？
(2)班车从A城到C城共行驶2 h,到C城后还能接收到该无线电信号发射塔发出的信号吗？请说明理由.

答案：
（1）如图,过点B作BM⊥AC于点M.
∵ 班车行驶了0.5 h时,接收信号最强,
∴ 此时班车到达点M处.又
∵ AM=60×0.5=30(km),AB=50 km,
∴ BM=√(AB²-AM²)=40 km.
∴ 此时班车到发射塔的距离是40 km （2）能 理由:如图,连结BC.
∵ AC=60×2=120(km),AM=30 km,
∴ CM=AC-AM=90 km.
∴ BC=√(BM²+CM²)=10√97 km,
∵ 10√97＜100,
∴ 到C城后还能接收到该无线电信号发射塔发出的信号.