《2025年通城学典课时作业本九年级数学全一册浙教版》

$\sin 30^{\circ}=$$\frac{1}{2}$,$\cos 30^{\circ}=$$\frac{\sqrt{3}}{2}$,$\tan 30^{\circ}=$$\frac{\sqrt{3}}{3}$；$\sin 60^{\circ}=$$\frac{\sqrt{3}}{2}$,$\cos 60^{\circ}=$$\frac{1}{2}$,$\tan 60^{\circ}=$$\sqrt{3}$；$\sin 45^{\circ}=$$\frac{\sqrt{2}}{2}$,$\cos 45^{\circ}=$$\frac{\sqrt{2}}{2}$,$\tan 45^{\circ}=$1.

答案： $\frac{1}{2}$，$\frac{\sqrt{3}}{2}$，$\frac{\sqrt{3}}{3}$；$\frac{\sqrt{3}}{2}$，$\frac{1}{2}$，$\sqrt{3}$；$\frac{\sqrt{2}}{2}$，$\frac{\sqrt{2}}{2}$，1

1. (2024·天津)$\sqrt{2}\cos 45^{\circ}-1$的值等于(A)
A.0
B.1
C.$\frac{\sqrt{2}}{2}-1$
D.$\sqrt{2}-1$

答案： A

2. 已知$\alpha$为锐角,且$\cos\alpha=\frac{\sqrt{3}}{2}$,则$\alpha$等于(A)
A.$30^{\circ}$
B.$45^{\circ}$
C.$60^{\circ}$
D.$90^{\circ}$

答案： A

3. 在$\text{Rt}\triangle ABC$中,$\angle C= 90^{\circ}$,$\angle B= 30^{\circ}$,$AB= 8$,则$BC$的长为(D)
A.$\frac{4\sqrt{3}}{3}$
B.4
C.$8\sqrt{3}$
D.$4\sqrt{3}$

答案： D

4. 在$\triangle ABC$中,若$\angle A= 105^{\circ}$,$\angle B= 45^{\circ}$,则$\tan C$的值为$\frac{\sqrt{3}}{3}$.

答案： $\frac{\sqrt{3}}{3}$

5. 计算：
(1)$\frac{2\cos^{2}30^{\circ}-\sin 30^{\circ}}{\tan^{2}60^{\circ}-4\cos 45^{\circ}}$；
(2)$2\cos 45^{\circ}\cdot\sin 45^{\circ}-2\sin 30^{\circ}\cdot\tan 45^{\circ}+\sqrt{6}\tan 60^{\circ}$.

答案： （1）原式$=\frac{2×\left(\frac{\sqrt{3}}{2}\right)^2-\frac{1}{2}}{(\sqrt{3})^2-4×\frac{\sqrt{2}}{2}}=\frac{2×\frac{3}{4}-\frac{1}{2}}{3-2\sqrt{2}}=\frac{1}{3-2\sqrt{2}}=3+2\sqrt{2}$；（2）原式$=2×\frac{\sqrt{2}}{2}×\frac{\sqrt{2}}{2}-2×\frac{1}{2}×1+\sqrt{6}×\sqrt{3}=1-1+3\sqrt{2}=3\sqrt{2}$

6. (2024·宁波鄞州期末)$\triangle ABC的两个锐角\angle A和\angle B满足|\sin A-\frac{1}{2}|+(\tan B-1)^{2}= 0$,则$\angle C$的度数是______$105^{\circ}$.

答案： $105^{\circ}$

7. 若$\tan(\alpha+15^{\circ})= \sqrt{3}$,则$\tan\alpha$的值为1.

答案： 1

8. 设$\alpha$为锐角,若$\cos^{2}\alpha=\frac{3}{4}$,则$\alpha=$$30^{\circ}$；若$\tan(\alpha-10^{\circ})= \frac{\sqrt{3}}{3}$,则$\alpha=$$40^{\circ}$.

答案： $30^{\circ}$；$40^{\circ}$

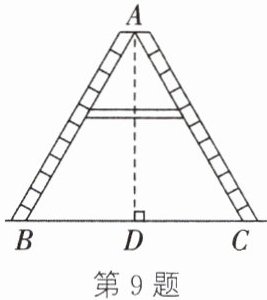
9. 如图,梯子$AB$,$AC的长均为3.2\ \text{m}$,当梯子的顶端离地面的高度$AD为\frac{8\sqrt{3}}{5}\ \text{m}$时,求：
(1)$\angle ACB$的度数；
(2)梯脚$B与C$之间的距离.

答案： （1）$\because$ 在 $\text{Rt}\triangle ACD$ 中，$AD=\frac{8\sqrt{3}}{5}\ \text{m}$，$AC=3.2\ \text{m}$，$\therefore \sin\angle ACB=\frac{AD}{AC}=\frac{\frac{8\sqrt{3}}{5}}{3.2}=\frac{\sqrt{3}}{2}$．$\because \angle ACB$ 为锐角，$\therefore \angle ACB=60^{\circ}$；（2）由（1），得$\angle ACB=60^{\circ}$．又$\because AB=AC$，$\therefore \triangle ABC$ 是等边三角形，$\therefore BC=AB=3.2\ \text{m}$．$\therefore$ 梯脚 B 与 C之间的距离为 $3.2\ \text{m}$