第67页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
6. 如图,某建筑物的顶部有一块宣传牌CD,小明在山坡的坡脚A处测得宣传牌底部D的仰角为60°,沿山坡向上走到B处测得宣传牌顶部C的仰角为45°,已知斜坡AB的坡角为30°,AB= 10米,AE= 15米,则宣传牌CD的高度是 (
A.$(20-10\sqrt{3})$米
B.$(20+5\sqrt{3})$米
C.$(15+5\sqrt{3})$米
D.$(15\sqrt{3}-5)$米
A
)A.$(20-10\sqrt{3})$米
B.$(20+5\sqrt{3})$米
C.$(15+5\sqrt{3})$米
D.$(15\sqrt{3}-5)$米
答案:
A
7. (2023·眉山)如图,一渔船在海上A处测得灯塔C在它的北偏东60°方向,渔船向正东方向航行12海里到达点B处,测得灯塔C在它的北偏东45°方向.若渔船继续向正东方向航行,则渔船与灯塔C的最短距离是
$6\sqrt{3}+6$
海里.
答案:
$(6\sqrt{3}+6)$
8. (2024·通辽)在综合与实践活动课上,活动小组测量一棵垂直于水平面的树的高度.如图,在点C处测得树底端点B的仰角是30°,$BC= 6$米,在与点C相距4米的点D处测得树顶端点A的仰角为45°,AB,BC,CD在同一平面内,点C,D在同一水平线上,求树AB的高度(结果精确到0.1米,参考数据:$\sqrt{3}\approx1.73$).
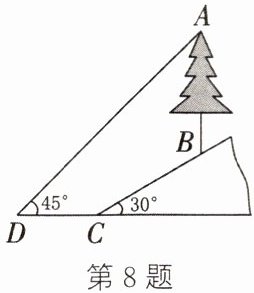

答案:
延长$AB$交直线$DC$于点$H$,则$\angle AHD = 90^{\circ}$。因为$\angle BCH = 30^{\circ}$,$BC = 6$米,所以易得$BH = \frac{1}{2}BC = 3$米,$CH = \frac{\sqrt{3}}{2}BC = 3\sqrt{3}$米。因为$\angle ADC = 45^{\circ}$,所以$AH = DH = CD + CH = (4 + 3\sqrt{3})$米,所以$AB = AH - BH = 4 + 3\sqrt{3}-3 = 1 + 3\sqrt{3}\approx6.2$(米),所以树$AB$的高度约为$6.2$米。
9. 如图,公路AB为东西走向,在点A的北偏东36.5°方向,距离点A5 km处是村庄M;在点A的北偏东53.5°方向,距离点A10 km处是村庄N(参考数据:$\sin36.5°\approx0.6$,$\cos36.5°\approx0.8$).
(1)求M,N两村庄之间的距离;
(2)要在公路AB旁修建一个收购站P,使得M,N两村庄到收购站P的距离之和最小,求这个最小距离之和.
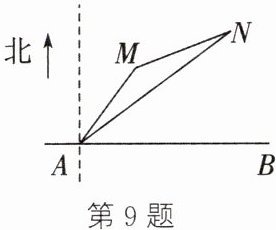
(1)求M,N两村庄之间的距离;
(2)要在公路AB旁修建一个收购站P,使得M,N两村庄到收购站P的距离之和最小,求这个最小距离之和.

答案:
(1)如图,过点$N$作$NE\perp AB$于点$E$,过点$M$作$CD// AB$,交过点$A$的$AB$的垂线于点$C$,交$NE$于点$D$,则$\angle ACD = \angle CDN = 90^{\circ}$,易得四边形$CAED$为矩形。由题意,得$\angle CAM = 36.5^{\circ}$,$\angle CAN = 53.5^{\circ}$,$AM = 5\mathrm{km}$,$AN = 10\mathrm{km}$。所以$CM = AM\cdot\sin36.5^{\circ}\approx5×0.6 = 3(\mathrm{km})$,所以$AC = \sqrt{AM^{2}-CM^{2}} = 4\mathrm{km}$。在$Rt\triangle ANE$中,$\angle NAE = 90^{\circ}-53.5^{\circ}=36.5^{\circ}$,$AN = 10\mathrm{km}$,所以$NE = AN\cdot\sin36.5^{\circ}\approx10×0.6 = 6(\mathrm{km})$,所以$AE = \sqrt{AN^{2}-NE^{2}} = 8\mathrm{km}$。因为四边形$CAED$为矩形,所以易得$MD = CD - CM = AE - CM = 5\mathrm{km}$,$ND = NE - DE = NE - AC = 2\mathrm{km}$。所以在$Rt\triangle MND$中,$MN = \sqrt{MD^{2}+ND^{2}} = \sqrt{29}\mathrm{km}$,所以$M$,$N$两村庄之间的距离约为$\sqrt{29}\mathrm{km}$。
(2)如图,作点$N$关于$AB$的对称点$G$,连结$MG$交$AB$于点$P$,连结$NP$,则$P$为站点,此时$PM + PN = PM + PG = MG$。易得$DG = DE + EG = DE + NE = 10\mathrm{km}$。在$Rt\triangle MDG$中,$MG = \sqrt{5^{2}+10^{2}} = 5\sqrt{5}(\mathrm{km})$,所以$M$,$N$两村庄到收购站$P$的距离之和最小约为$5\sqrt{5}\mathrm{km}$。
(2)如图,作点$N$关于$AB$的对称点$G$,连结$MG$交$AB$于点$P$,连结$NP$,则$P$为站点,此时$PM + PN = PM + PG = MG$。易得$DG = DE + EG = DE + NE = 10\mathrm{km}$。在$Rt\triangle MDG$中,$MG = \sqrt{5^{2}+10^{2}} = 5\sqrt{5}(\mathrm{km})$,所以$M$,$N$两村庄到收购站$P$的距离之和最小约为$5\sqrt{5}\mathrm{km}$。
查看更多完整答案,请扫码查看


