第40页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
1. 如图,正六边形 ABCDEF 内接于$\odot O$,Q 是$\widehat{DE}$的中点,P 是$\widehat{AF}$上的一个动点,则$\angle CPQ$的度数为 (
A.$30^{\circ}$
B.$36^{\circ}$
C.$45^{\circ}$
D.$60^{\circ}$
C
)A.$30^{\circ}$
B.$36^{\circ}$
C.$45^{\circ}$
D.$60^{\circ}$
答案:
C
2. 如图,有一块形状为等边三角形的木板,边长为 1,现将木板沿水平线翻滚,则点 B 从开始至结束所经过的路径长为 (
A.$\frac{3\pi}{2}$
B.$\frac{4\pi}{3}$
C.4
D.$2+\frac{3\pi}{2}$
B
)A.$\frac{3\pi}{2}$
B.$\frac{4\pi}{3}$
C.4
D.$2+\frac{3\pi}{2}$
答案:
B
3. (2023·安徽)如图,矩形 ABCD 内接于$\odot O$,分别以 AB,BC,CD,AD 为直径向外作半圆. 若$AB= 4$,$BC= 5$,则涂色部分的面积是 (
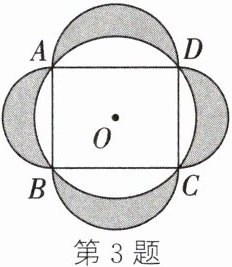
A.$\frac{41\pi}{4}-20$
B.$\frac{41\pi}{2}-20$
C.$20\pi$
D.20
D
)
A.$\frac{41\pi}{4}-20$
B.$\frac{41\pi}{2}-20$
C.$20\pi$
D.20
答案:
D
4. 如图,在矩形 ABCD 中,$AB= 6$,$BC= 8$,将矩形 ABCD 绕点 D 旋转$180^{\circ}$后停止,则矩形 ABCD 在旋转过程中扫过的面积为
48+50π
.
答案:
48+50π 解析:矩形ABCD在旋转过程中扫过的面积是矩形ABCD的面积与半径为BD的半圆的面积之和
5. (2023·仙桃)如图,在$3×3$的正方形网格中,小正方形的顶点称为格点,顶点均在格点上的图形称为格点图形,图中的圆弧为格点三角形 ABC 外接圆的一部分,每个小正方形的边长均为 1,则图中涂色部分的面积为(
A.$\frac{5\pi}{2}-\frac{7}{4}$
B.$\frac{5\pi}{2}-\frac{7}{2}$
C.$\frac{5\pi}{4}-\frac{7}{4}$
D.$\frac{5\pi}{4}-\frac{7}{2}$
D
)A.$\frac{5\pi}{2}-\frac{7}{4}$
B.$\frac{5\pi}{2}-\frac{7}{2}$
C.$\frac{5\pi}{4}-\frac{7}{4}$
D.$\frac{5\pi}{4}-\frac{7}{2}$
答案:
D
6. 如图,在正方形网格中,每个小正方形的边长均为 1,$\triangle ABC和\triangle A'B'C'$的各个顶点均在格点处,且$\triangle A'B'C'是由\triangle ABC$以网格中的某个格点为旋转中心,按逆时针方向旋转$90^{\circ}$得到的. 已知点 A,B,C 的对应点分别为$A'$,$B'$,$C'$,则在旋转过程中,点 A 所经过的路径长为______
$\frac{\sqrt{10}\pi}{2}$
.
答案:
$\frac{\sqrt{10}\pi}{2}$
7. (易错题)(2023·乐山改编)如图,在$\triangle ABC$中,$AB= 4$,$AC= 6$. 将$\triangle ABC$绕点 A 逆时针旋转$40^{\circ}$,在运动过程中,边 AC 扫过的面积为______
4π
,点 B 运动的路径长为______$\frac{8}{9}$π
.
答案:
4π $\frac{8}{9}$π [易错分析]第1空求的是扇形面积,而第2空求的是扇形弧长,两个公式不能互相混淆.
8. 如图,在$Rt\triangle ABC$中,$\angle ACB= 90^{\circ}$,$AC= BC= 2$. 将$\triangle ABC$绕 AC 的中点 D 按逆时针方向旋转$90^{\circ}得到\triangle A'B'C'$,其中点 B 的运动路径为$\widehat{BB'}$. 求涂色部分的面积.
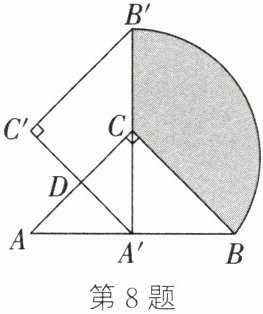

答案:
如图,连结BD,B'D.由旋转的性质可知,$\triangle BCD\cong\triangle B'C'D$,$\angle BDB'=\angle CDC'=90^\circ$,$BC=B'C'=2$,$CD=C'D$.
∵D为AC 的中点,
∴$C'D=CD=\frac{1}{2}AC=1$.
∴在Rt△BCD中,由勾股定理,得$BD=\sqrt{BC^2+CD^2}=\sqrt{2^2+1^2}=\sqrt{5}$.$\therefore S_{\text{扇形}BDB'}=\frac{90\pi×(\sqrt{5})^2}{360}=\frac{5\pi}{4}$.$\because\triangle BCD\cong\triangle B'C'D$,$\therefore S_{\triangle BCD}=S_{\triangle B'C'D}$.易得四边形CDC'B'为梯形,$\therefore S_{\triangle BCD}+S_{\triangle B'C'D}=S_{\triangle B'C'D}+S_{\triangle BCD}=S_{\text{梯形}CDC'B'}=\frac{1}{2}C'D\cdot(CD+B'C')=\frac{1}{2}×1×(1+2)=\frac{3}{2}$.$\therefore S_{\text{涂色部分}}=S_{\text{扇形}BDB'}-(S_{\triangle BCD}+S_{\triangle B'C'D})=S_{\text{扇形}BDB'}-S_{\text{梯形}CDC'B'}=\frac{5\pi}{4}-\frac{3}{2}$

如图,连结BD,B'D.由旋转的性质可知,$\triangle BCD\cong\triangle B'C'D$,$\angle BDB'=\angle CDC'=90^\circ$,$BC=B'C'=2$,$CD=C'D$.
∵D为AC 的中点,
∴$C'D=CD=\frac{1}{2}AC=1$.
∴在Rt△BCD中,由勾股定理,得$BD=\sqrt{BC^2+CD^2}=\sqrt{2^2+1^2}=\sqrt{5}$.$\therefore S_{\text{扇形}BDB'}=\frac{90\pi×(\sqrt{5})^2}{360}=\frac{5\pi}{4}$.$\because\triangle BCD\cong\triangle B'C'D$,$\therefore S_{\triangle BCD}=S_{\triangle B'C'D}$.易得四边形CDC'B'为梯形,$\therefore S_{\triangle BCD}+S_{\triangle B'C'D}=S_{\triangle B'C'D}+S_{\triangle BCD}=S_{\text{梯形}CDC'B'}=\frac{1}{2}C'D\cdot(CD+B'C')=\frac{1}{2}×1×(1+2)=\frac{3}{2}$.$\therefore S_{\text{涂色部分}}=S_{\text{扇形}BDB'}-(S_{\triangle BCD}+S_{\triangle B'C'D})=S_{\text{扇形}BDB'}-S_{\text{梯形}CDC'B'}=\frac{5\pi}{4}-\frac{3}{2}$

查看更多完整答案,请扫码查看


