《2025年通城学典课时作业本九年级数学全一册浙教版》

16..如图,在平面直角坐标系中,正方形ABCD与正方形BEFG是以原点O为位似中心的位似图形,且位似比为$\frac{1}{3}$,点A,B,E在x轴上,若正方形BEFG的边长6,则点C的坐标为(3,2).

答案： (3,2)

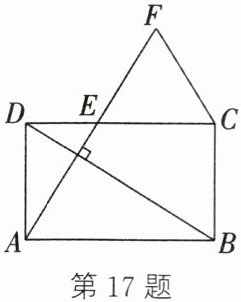
17.(2024·上海)如图,在矩形ABCD中,E边CD上一点,且AE⊥BD.
(1)求证:$AD^{２}=DE·DC$;
(２)F线段AE延长线上一点,且满足$EF= CF= \frac{1}{2}BD$,求证:CE= AD.

答案：
(1)
∵四边形ABCD是矩形,
∴∠BAD=90°,∠ADE=90°,AB=DC.
∴∠ABD+∠ADB=90°.
∵AE⊥BD,
∴∠DAE+∠ADB=90°.
∴∠DAE=∠ABD.
∵∠ADE=∠BAD=90°,
∴△ADE∽△BAD.
∴AD/BA=DE/AD.
∴AD²=DE·BA.
∵AB=DC,
∴AD²=DE·DC
(2)连结AC,交BD于点O.由
(1)知,△ADE∽△BAD,
∴∠DEA=∠ADB.
∵∠FEC=∠DEA,
∴∠ADO=∠FEC.
∵四边形ABCD是矩形,
∴OA=OD=1/2BD.又
∵EF=CF=1/2BD,
∴OA=OD=EF=CF.
∴∠ADO=∠OAD,∠FEC=∠FCE.
∵∠ADO=∠FEC,
∴∠ADO=∠OAD=∠FEC=∠FCE.在△FEC和△ODA中,{∠FEC=∠ODA,∠FCE=∠OAD,FE=OD,}
∴△FEC≌△ODA.
∴CE=AD

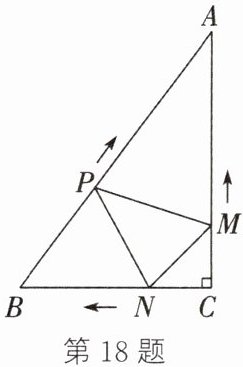
18.如图,在Rt△ABC中,∠C= 90°,AC= 4 cm,BC= 3 cm.动点M,N从点C同时出发,均以1 cm/s 的速度分别沿CA,CB向点A,B移动.同时,动点P从点B出发.以2 cm/s 的速度沿BA向点A移动.连结PM,PN,NM,设移动时间为t s(0＜t＜2.5).
(1)当t为何值时.以A,P,M为顶点的三角形与△ABC相似?
(2)设四边形APNC的面积为$S cm^2.$是否存在t的值,使S取得最小值?若存在.求出S的最小值；若不存在,请说明理由.

答案：
(1)
∵在Rt△ABC中,∠C=90°,AC=4 cm,BC=3 cm,
∴AB=√(AC²+BC²)=5 cm.由题意,得CN=CM=t cm,AM=(4-t) cm,BN=(3-t) cm,BP=2t cm,AP=(5-2t) cm. 分两种情况讨论:①当△AMP∽△ABC时,AP/AC=AM/AB,即(5-2t)/4=(4-t)/5,解得t=3/2;②当△APM∽△ABC时,AM/AC=AP/AB,即(4-t)/4=(5-2t)/5,解得t=0(不合题意,舍去).综上所述,当t=3/2时,以A,P,M为顶点的三角形与△ABC相似
(2)存在 过点P作PH⊥BC于点H,则∠PHB=90°.
∵∠C=90°,
∴∠PHB=∠C.又
∵∠B=∠B,
∴△BPH∽△BAC.
∴PH/AC=BP/BA.
∴PH=8/5t cm.
∴S=1/2×3×4 - 1/2×(3-t)×8/5t=4/5t² - 12/5t + 6=4/5(t - 3/2)² + 21/5.
∵4/5＞0,0＜t＜2.5,
∴当t=3/2时,S取得最小值,为21/5