第54页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
相似三角形的周长和面积有以下性质:相似三角形的周长之比等于
相似比
;相似三角形的面积之比等于相似比的平方
.
答案:
相似比 相似比的平方
1. (2024·重庆 A 卷)若两个相似三角形的相似比是1:3,则这两个相似三角形的面积之比为(
A.1:3
B.1:4
C.1:6
D.1:9
D
)A.1:3
B.1:4
C.1:6
D.1:9
答案:
D
2. 若△ABC∽△DEF,且面积之比为9:4,则它们的对应高线长的比为(
A.3:2
B.2:3
C.9:4
D.4:9
A
)A.3:2
B.2:3
C.9:4
D.4:9
答案:
【解析】:
本题主要考察相似三角形的性质,特别是相似三角形的面积比与对应边长(包括高线)比的关系。
根据相似三角形的性质,如果两个三角形相似,那么它们的面积之比等于它们对应边长之比的平方。
设相似三角形$\bigtriangleup ABC$和$\bigtriangleup DEF$的对应边长之比为$k$,则它们的面积之比为$k^2$。
题目给出面积之比为$9:4$,即$k^2 = \frac{9}{4}$。
解这个方程,我们得到$k = \frac{3}{2}$(负值舍去,因为边长不能为负)。
由于高线也是三角形的一边,所以对应高线的比也等于$k$,即$3:2$。
【答案】:
A
本题主要考察相似三角形的性质,特别是相似三角形的面积比与对应边长(包括高线)比的关系。
根据相似三角形的性质,如果两个三角形相似,那么它们的面积之比等于它们对应边长之比的平方。
设相似三角形$\bigtriangleup ABC$和$\bigtriangleup DEF$的对应边长之比为$k$,则它们的面积之比为$k^2$。
题目给出面积之比为$9:4$,即$k^2 = \frac{9}{4}$。
解这个方程,我们得到$k = \frac{3}{2}$(负值舍去,因为边长不能为负)。
由于高线也是三角形的一边,所以对应高线的比也等于$k$,即$3:2$。
【答案】:
A
3. 已知△FHB∽△EAD,它们的周长分别为30 和15,且FH= 6,则EA 的长为(
A.2
B.3
C.4
D.5
B
)A.2
B.3
C.4
D.5
答案:
B
4. 如图,在□ABCD 中,F 为BC 的中点,延长AD 至点E,使DE:AD= 1:3,连结EF 交CD 于点G,则S△DEG:S△CFG 等于(
A.2:3
B.3:2
C.9:4
D.4:9
D
)A.2:3
B.3:2
C.9:4
D.4:9
答案:
D
5. (2024·辽宁)如图,AB//CD,AD 与BC 相交于点O,且△AOB 与△DOC 的面积之比为1:4.若AB= 6,则CD 的长为
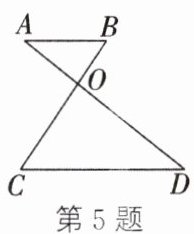
12
.
答案:
12
6. (2024·云南)如图,AB 与CD 交于点O,且AC//BD.若$\frac{OA+OC+AC}{OB+OD+BD}= \frac{1}{2}$,则$\frac{AC}{BD}= $
$\frac{1}{2}$
.
答案:
$\frac{1}{2}$
7. (2024·乐山)如图,在梯形ABCD 中,AD//BC,对角线AC 和BD 交于点O.若$\frac{S_{\triangle ABD}}{S_{\triangle BCD}}= \frac{1}{3}$,则$\frac{S_{\triangle AOD}}{S_{\triangle BOC}}=$
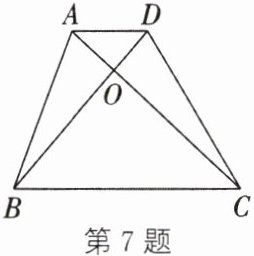
$\frac{1}{9}$
.
答案:
$\frac{1}{9}$
8. 如图,把△ABC 沿边AB 平移到△A'B'C'的位置,它们重叠部分(即图中涂色部分)的面积是△ABC 的面积的一半.若$AB= \sqrt{2}$,则AA'的长为
$\sqrt{2}-1$
.
答案:
$\sqrt{2}-1$
9. 如图,在△ABC 和△DEC 中,∠A= ∠D,∠BCE= ∠ACD.
(1)求证:△ABC∽△DEC;
(2)若$S_{\triangle ABC}:S_{\triangle DEC}= 4:9$,$BC= 6$,求EC的长.
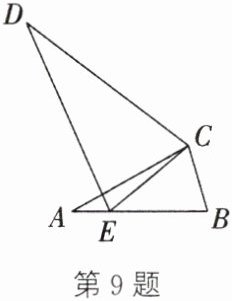
(1)求证:△ABC∽△DEC;
(2)若$S_{\triangle ABC}:S_{\triangle DEC}= 4:9$,$BC= 6$,求EC的长.

答案:
(1)$\because \angle BCE=\angle ACD$,$\therefore \angle BCE+\angle ACE=\angle ACD+\angle ACE$,即$\angle ACB=\angle DCE$.又$\because \angle A=\angle D$,$\therefore \triangle ABC\backsim \triangle DEC$ (2)$\because \triangle ABC\backsim \triangle DEC$,$\therefore \frac{S_{\triangle ABC}}{S_{\triangle DEC}}=\left( \frac{BC}{EC} \right)^{2}$.$\because S_{\triangle ABC}:S_{\triangle DEC}=4:9$,即$\frac{S_{\triangle ABC}}{S_{\triangle DEC}}=\frac{4}{9}$,$\therefore \frac{BC}{EC}=\frac{2}{3}$.$\because BC=6$,$\therefore EC=9$
查看更多完整答案,请扫码查看


