《2025年假期面对面南方出版社七年级数学沪科版》

10. (1)$6^{\circ }30'18''=$6.505$^{\circ }$;
(2)$37.145^{\circ }=$37$^{\circ }$8$'$42$''$.

答案：
(1) 6.505
(2) 37 8 42

11. 一个角的补角比它的余角的2倍多$30^{\circ }$,这个角的度数为$30^{\circ}$.

答案： $30^{\circ}$

12. 如图,点B是线段AC上的点,图中共有3条线段.

答案： 3

13. 如图,D是AB的中点,E是BC的中点,$AE=10,CD=8$,则线段DE的长为____6.

答案： 6

14. (8分)情景一:如图,从教学楼到图书馆,总有少数同学不走人行道而横穿草坪,这是为什么呢?试用所学数学知识来说明这个问题.

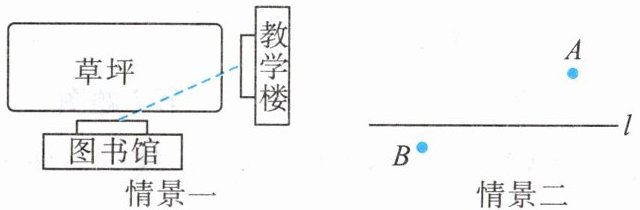
情景二:如图,A,B是河流l两旁的两个村庄,现要在河边修一个抽水站向两村供水,问抽水站修在什么地方才能使所需的管道最短?请在图中表示出抽水站点P的位置,并说明你的理由.
你赞同以上哪种做法?

答案：
解: 情景一: 横穿草坪是为了所走路程最短. 因为两点之间的所有连线中, 线段最短. 理由: 两点之间的所有连线中，线段最短,赞同情景二中的做法.

15. (12分)如图,已知线段$AB=8$,点C是线段AB的中点,点D是线段BC的中点.
(1)求线段AD的长;6
(2)若在线段AC上有一点E,$CE=\frac {1}{4}BC$,求线段AE的长.3

答案： 解:
(1) 因为点 $C$ 是 $AB$ 的中点, 点 $D$ 是 $BC$ 的中点, $AB = 8$, 所以 $AC = BC = \frac{1}{2}AB = \frac{1}{2} \times 8 = 4$, $CD = \frac{1}{2}BC = \frac{1}{2} \times 4 = 2$, 所以 $AD = AC + CD = 4 + 2 = 6$.
(2) 如图,
因为 $CE = \frac{1}{4}BC$, $BC = 4$, 所以 $CE = \frac{1}{4} \times 4 = 1$, 所以 $AE = AC - CE = 4 - 1 = 3$.

16. (14分)如图,已知O为直线AD上一点,OC是$∠AOB$内部的一条射线且满足$∠AOB$与$∠AOC$互补,OM,ON分别为$∠AOB,∠AOC$的角平分线.
(1)$∠COD$与$∠AOB$相等吗?为什么?
答：相等，理由如下:
因为 $ \angle AOB $ 与 $ \angle AOC $ 互补, 所以 $ \angle AOB + \angle AOC = 180^{\circ} $.
因为 $ \angle COD + \angle AOC = 180^{\circ} $, 所以 $ \angle COD = \angle AOB $.
(2)若$∠AOB=150^{\circ }$,试求$∠AON$与$∠MON$的度数;
答：$∠AON$的度数为15°，$∠MON$的度数为60°
(3)若$∠MON=52^{\circ }$,试求$∠AOB$的度数.
答：$∠AOB$的度数为142°

答案： 解:
(1) $ \angle COD = \angle AOB $, 理由如下:
因为 $ \angle AOB $ 与 $ \angle AOC $ 互补, 所以 $ \angle AOB + \angle AOC = 180^{\circ} $.
因为 $ \angle COD + \angle AOC = 180^{\circ} $, 所以 $ \angle COD = \angle AOB $.
(2) 因为 $ \angle AOB $ 与 $ \angle AOC $ 互补, $ \angle AOB = 150^{\circ} $, 所以 $ \angle AOC = 180^{\circ} - 150^{\circ} = 30^{\circ} $. 因为 $ON$ 为 $ \angle AOC $ 的角平分线, 所以 $ \angle AON = \frac{1}{2}\angle AOC = \frac{1}{2} \times 30^{\circ} = 15^{\circ} $. 因为 $OM$ 为 $ \angle AOB $ 的角平分线, $ \angle AOB = 150^{\circ} $, 所以 $ \angle AOM = \frac{1}{2}\angle AOB = \frac{1}{2} \times 150^{\circ} = 75^{\circ} $, 所以 $ \angle MON = \angle AOM - \angle AON = 75^{\circ} - 15^{\circ} = 60^{\circ} $.
(3) 因为 $OM$, $ON$ 分别为 $ \angle AOB $, $ \angle AOC $ 的角平分线, 所以 $ \angle AOM = \frac{1}{2}\angle AOB $, $ \angle AON = \frac{1}{2}\angle AOC $, 所以 $ \angle MON = \angle AOM - \angle AON = \frac{1}{2}\angle AOB - \frac{1}{2}\angle AOC = 52^{\circ} $, 所以 $ \angle AOB - \angle AOC = 104^{\circ} $. 又因为 $ \angle AOB + \angle AOC = 180^{\circ} $, 所以 $ \angle AOB = 142^{\circ} $.