2025年假期面对面南方出版社七年级数学沪科版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年假期面对面南方出版社七年级数学沪科版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第4页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
16. 若a,b为两个连续整数,且$a<\sqrt {3}<b$,则$a+b=$
3
.
答案:
3
17. 若$|a-1|+(b-3)^{2}=0$,则$\sqrt {a+b}=$
2
.
答案:
2
18. 如图,将数$-\sqrt {5},\sqrt {7},\sqrt {13}$表示在数轴上,其中能被墨迹覆盖的数是
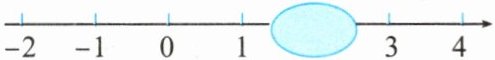
$\sqrt{7}$
.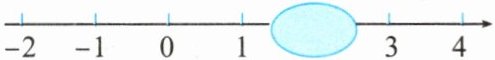
答案:
$\sqrt{7}$
19. 如图,点A,B,C在数轴上,点A表示的数是-1,点B是AC的中点,线段$AB=\sqrt {2}$,则点C表示的数是
$2 \sqrt{2}-1$
.
答案:
$2 \sqrt{2}-1$
20. (4分)把下列各数填入相应的集合内.
$-\frac {1}{2},-\sqrt {3},\frac {\sqrt {2}}{3},\sqrt {\frac {81}{4}},-\sqrt [3]{-8},0,-π,-\frac {117}{3},-4.\dot {2}0\dot {1}.$
(1)整数集合:{ …};
(2)分数集合:{ …};
(3)有理数集合:{ …};
(4)无理数集合:{ …}.
$-\frac {1}{2},-\sqrt {3},\frac {\sqrt {2}}{3},\sqrt {\frac {81}{4}},-\sqrt [3]{-8},0,-π,-\frac {117}{3},-4.\dot {2}0\dot {1}.$
(1)整数集合:{ …};
(2)分数集合:{ …};
(3)有理数集合:{ …};
(4)无理数集合:{ …}.
答案:
解:
(1) $-\sqrt[3]{-8}, 0$
(2) $-\frac{1}{2}, \sqrt{\frac{81}{4}},-\frac{117}{3},-4 . \dot{2} 0 \dot{1}$
(3) $-\frac{1}{2}, \sqrt{\frac{81}{4}},-\sqrt[3]{-8}, 0,-\frac{117}{3},-4 . \dot{2} 0 \dot{1}$
(4) $-\sqrt{3}, \frac{\sqrt{2}}{3},-\pi$
(1) $-\sqrt[3]{-8}, 0$
(2) $-\frac{1}{2}, \sqrt{\frac{81}{4}},-\frac{117}{3},-4 . \dot{2} 0 \dot{1}$
(3) $-\frac{1}{2}, \sqrt{\frac{81}{4}},-\sqrt[3]{-8}, 0,-\frac{117}{3},-4 . \dot{2} 0 \dot{1}$
(4) $-\sqrt{3}, \frac{\sqrt{2}}{3},-\pi$
21. (3分)计算:
(1)$(-1)^{2025}+\sqrt {16}-|-3|;$
(2)$3^{2}+\sqrt [3]{-64}-\sqrt {25};$
(3)$-4^{2}+16÷\sqrt {(-2)^{2}}×\frac {1}{2}.$
(1)$(-1)^{2025}+\sqrt {16}-|-3|;$
(2)$3^{2}+\sqrt [3]{-64}-\sqrt {25};$
(3)$-4^{2}+16÷\sqrt {(-2)^{2}}×\frac {1}{2}.$
答案:
解:
(1) 原式 $=-1+4-3=0$.
(2) 原式 $=9-4-5=0$.
(3) 原式 $=-16+16 \div 2 \times \frac{1}{2}=-16+4=-12$.
(1) 原式 $=-1+4-3=0$.
(2) 原式 $=9-4-5=0$.
(3) 原式 $=-16+16 \div 2 \times \frac{1}{2}=-16+4=-12$.
22. (6分)已知$3a-7$和$a+3$是正数m的两个不同的平方根,$b+4$的立方根为2,c是$\sqrt {11}$的整数部分.求:
(1)m的值;
(2)$a+3b+c$的平方根.
(1)m的值;
(2)$a+3b+c$的平方根.
答案:
解:
(1) 因为 $3 a-7$ 和 $a+3$ 是正数 $m$ 的两个平方根, 所以 $3 a-7+a+3=0$, 所以 $a=1$, 所以 $a+3=1+3=4$, 所以 $m=16$.
(2) 因为 $b+4$ 的立方根为 2 , 所以 $b+4=8$, 所以 $b=4$. 因为 $3<\sqrt{11}<4$, 所以 $\sqrt{11}$ 的整数部分 $c=3$, 所以 $a+3 b+c=1+3 \times 4+3=16$, 所以 $a+3 b+c$ 的平方根是 $\pm 4$.
(1) 因为 $3 a-7$ 和 $a+3$ 是正数 $m$ 的两个平方根, 所以 $3 a-7+a+3=0$, 所以 $a=1$, 所以 $a+3=1+3=4$, 所以 $m=16$.
(2) 因为 $b+4$ 的立方根为 2 , 所以 $b+4=8$, 所以 $b=4$. 因为 $3<\sqrt{11}<4$, 所以 $\sqrt{11}$ 的整数部分 $c=3$, 所以 $a+3 b+c=1+3 \times 4+3=16$, 所以 $a+3 b+c$ 的平方根是 $\pm 4$.
23. (9分)如图,已知A,B,C三点分别对应数轴上的数a,b,c.
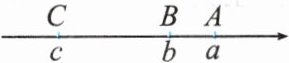
(1)化简:$|a-b|+|c-b|+|c-a|=$
(2)若$a=\frac {x+y}{4},b=-z^{2},c=-4mn$,且满足x与y互为相反数,z是绝对值最小的负整数,m,n互为倒数,试求$98a+99b+100c$的值为
(3)在(2)的条件下,在数轴上找一点D,满足D点表示的整数d到点A,点C的距离之和为10,则D点表示的整数为
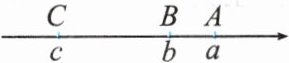
(1)化简:$|a-b|+|c-b|+|c-a|=$
2a-2c
;(2)若$a=\frac {x+y}{4},b=-z^{2},c=-4mn$,且满足x与y互为相反数,z是绝对值最小的负整数,m,n互为倒数,试求$98a+99b+100c$的值为
-499
;(3)在(2)的条件下,在数轴上找一点D,满足D点表示的整数d到点A,点C的距离之和为10,则D点表示的整数为
-7或3
.
答案:
解:
(1) 由数轴可知: $a-b>0, c-b<0, c-a<0$, 所以原式 $=(a-b)-(c-b)-(c-a)=a-b-c+b-c+a=2 a-2 c$.
(2) 由题意, 得 $x+y=0, z=-1, m n=1$. 所以 $a=0$, $b=-(-1)^2=-1, c=-4$. 所以原式 $=-99-400=$ -499.
(3) 满足条件的 $D$ 点表示的整数为 -7 或 3.
(1) 由数轴可知: $a-b>0, c-b<0, c-a<0$, 所以原式 $=(a-b)-(c-b)-(c-a)=a-b-c+b-c+a=2 a-2 c$.
(2) 由题意, 得 $x+y=0, z=-1, m n=1$. 所以 $a=0$, $b=-(-1)^2=-1, c=-4$. 所以原式 $=-99-400=$ -499.
(3) 满足条件的 $D$ 点表示的整数为 -7 或 3.
查看更多完整答案,请扫码查看


