《2025年假期面对面南方出版社七年级数学沪科版》

12. (长春中考)单项式$-2a^{2}b$的次数是____3.

答案： 3

13. (永州中考)若单项式$3x^{m}y$与$-2x^{6}y$是同类项,则$m=$6.

答案： 6

14. (吉林中考)篮球队要购买10个篮球,每个篮球$m$元,一共需要10m元. (用含$m$的代数式表示)

答案： $10m$

15. (绵阳中考)若多项式$xy^{|m-n|}+(n-2)x^{2}y^{2}+1$是关于$x,y$的三次多项式,则$mn=$0 或 8.

答案： 0 或 8

16. (天津中考)计算$4a+2a-a$的结果等于$5a$.

答案： $5a$

17. (苏州中考)若$a=b+2$,则$(b-a)^{2}=$4.

答案： 4

18. (广州中考)若$a^{2}-2a-5=0$,则$2a^{2}-4a+1=$11.

答案： 11

19. (江西中考)观察$a,a^{2},a^{3},a^{4},...$,根据这些式子的变化规律,可得第100个式子为$a^{100}$.

答案： $a^{100}$

20. (西藏中考)如图是由若干个大小相同的“○”组成的一组有规律的图案,其中第1个图案用了2个“○”,第2个图案用了6个“○”,第3个图案用了12个“○”,第4个图案用了20个“○”,…,依照此规律,第$n$个图案中“○”的个数为$n^{2}+n$. (用含$n$的代数式表示)

答案： $n^{2}+n$

21. (湖北中考)先化简,再求值:$4xy-2xy-(-3xy)$,其中$x=2,y=-1$.
解：原式 $=4xy - 2xy + 3xy =$5xy。当 $x = 2$，$y = -1$ 时，原式 $=5×2×(-1) =$-10。

答案： 解：原式 $=4xy - 2xy + 3xy = 5xy$。当 $x = 2$，$y = -1$ 时，原式 $=5×2×(-1) = -10$。

22. (河北中考)嘉淇准备完成题目:化简$(□x^{2}+6x+8)-(6x+5x^{2}+2)$. 发现系数“$□$”印刷不清楚.
(1)他把“$□$”里的数字猜成3,请你化简:$(3x^{2}+6x+8)-(6x+5x^{2}+2)$;
(2)他妈妈说:“你猜错了,我看到该题标准答案的结果是常数.”请你通过计算说明原题中“$□$”里的数字是几?

答案： 解：
(1) $(3x^{2}+6x + 8)-(6x + 5x^{2}+2)=3x^{2}+6x + 8 - 6x - 5x^{2}-2=-2x^{2}+6$。
(2) 设“$□$”是 $a$，则原式 $=(ax^{2}+6x + 8)-(6x + 5x^{2}+2)=ax^{2}+6x + 8 - 6x - 5x^{2}-2=(a - 5)x^{2}+6$。因为该题标准答案的结果是常数，所以 $a - 5 = 0$，所以 $a = 5$。故“$□$”里的数字是 5。

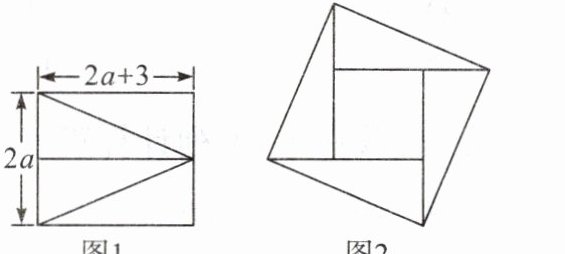
23. (金华中考)如图1,将长为$2a+3$,宽为$2a$的长方形分割成四个全等的直角三角形,拼成“赵爽弦图”(如图2),得到大小两个正方形.
(1)用含$a$的代数式表示图2中小正方形的边长;$a+3$
(2)当$a=3$时,该小正方形的面积是多少?36

答案： 解：
(1) 因为直角三角形较短的直角边 $=\frac{1}{2}×2a = a$，较长的直角边 $=2a + 3$，所以小正方形的边长 $=2a + 3 - a = a + 3$。
(2) 小正方形的面积 $=(a + 3)^{2}$，当 $a = 3$ 时，面积 $=(3 + 3)^{2}=36$。