《2025年假期面对面南方出版社七年级数学沪科版》

9. 若$(k + 2)x^{|k| - 1} - 2 = 6$是关于x的一元一次方程,则$k = $2.

答案： 2

10. 若一元一次方程$2x + a = 4$的解为$x = -1$,则a的值为6.

答案： 6

11. 若关于x,y的二元一次方程组$\left\{\begin{array}{l} 3x + y = 1 + 3a,\\ x + 3y = 1 - a\end{array}\right. $的解也是二元一次方程$x + y = 2$的解,则a的值为____3.

答案： 3

12. 《九章算术》中记载:“今有共买物,人出八,盈三;人出七,不足四. 问人数、物价各几何?”题目大意是:今有人合伙购物,每人出八钱,余三钱;每人出七钱,差四钱. 问:人数、物价各多少? 设有x人,物价为y钱,则可列方程组为$\begin{cases}8x - y = 3, \\ y - 7x = 4\end{cases}$.

答案： $\begin{cases}8x - y = 3, \\ y - 7x = 4\end{cases}$

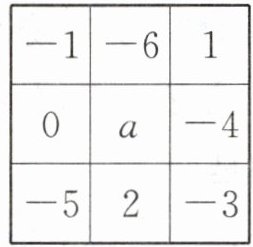
13. 幻方,最早源于我国,古人称之为纵横图.如图所示的幻方中,各行、各列及各条对角线上的三个数字之和均相等,则图中a的值为-2.

答案： $-2$

14. (10分)解方程(组):
(1)$4(y - 2) - 4 = y + 2(3 + y)$的解为$y = 18$;
(2)$\left\{\begin{array}{l} 2x + y = 7,\\ 2x - 3y = 3;\end{array}\right. $的解为$\begin{cases}x = 3, \\ y = 1\end{cases}$;
(3)$\left\{\begin{array}{l} x = y + z,\\ 3x + y = 18,\\ x + y + z = 10.\end{array}\right. $的解为$\begin{cases}x = 5, \\ y = 3, \\ z = 2\end{cases}$.

答案：
(1) $y = 18$
(2) $\begin{cases}x = 3, \\ y = 1\end{cases}$
(3) $\begin{cases}x = 5, \\ y = 3, \\ z = 2\end{cases}$

15. (12分)已知$(a + b)y^{2} - y^{\frac {1}{3}a + 2} + 5 = 0$是关于y的一元一次方程.
(1)求a,b的值;
(2)若$x = a$是关于x的方程$\frac {x + 2}{6} - \frac {x - 1}{2} + 3 = x - \frac {2x - m}{6}$的解,求$|a - b| - |b - m|$的值.
(1) $a=$-3，$b=$3；
(2) -32

答案： 解：
(1) 由题意知，$a + b = 0$，$\frac{1}{3}a + 2 = 1$，解得 $a = -3$，$b = 3$。
(2) 将 $x = a = -3$ 代入方程 $\frac{x + 2}{6} - \frac{x - 1}{2} + 3 = x - \frac{2x - m}{6}$，得 $-\frac{1}{6} + 2 + 3 = -3 - \frac{-6 - m}{6}$，解得 $m = 41$。所以 $|a - b| - |b - m| = |-3 - 3| - |3 - 41| =$

16. (12分)《张丘建算经》由北魏数学家张丘建所著,其中有这样一个问题:“今有客不知其数. 两人共盘,少两盘;三人共盘,长三盘. 问客及盘各几何?”意思为:“现有若干名客人. 若2个人共用1个盘子,则少2个盘子;若3个人共用1个盘子,则多出来3个盘子. 问客人和盘子各有多少?”请你解答这个问题.

答案： 解：设有 $x$ 个客人，$y$ 个盘子。由题意，得 $\begin{cases}\frac{x}{2} = y + 2, \\ \frac{x}{3} + 3 = y,\end{cases}$ 解得 $\begin{cases}x = 30, \\ y = 13.\end{cases}$ 答：有 30 个客人，13 个盘子。