第74页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
探究1 已知三角形三边长分别为2,x,13,若x为正整数,则这样的三角形个数为(
A.2
B.3
C.5
D.13
探究2 已知一等腰三角形一腰上的中线将此等腰三角形的周长分为7.5,15两部分,求此等腰三角形各边的长.
探究3 已知△ABC中,∠A= $\frac{2}{3}$∠B= $\frac{1}{2}$∠C.
(1)求∠A、∠B、∠C;
(2)若CD、CE分别是△ABC的高和角平分线,求∠DCE.
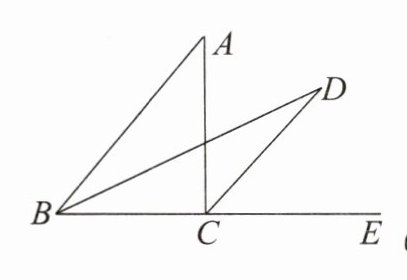
探究4 如图,△ABC中,∠A= 40°,点E在线段BC的延长线上,∠ABC的平分线和∠ACE的平分线相交于D,求∠D.
经典题组·新解读
1. 已知三角形两边的长a、b(a>b),求第三边x的取值范围是一个常见题型,它直接考查了
其一般解法是
2. (1)对于探究2你做的第一步工作是什么?
温馨提示:根据题意画出图形既是解题的基础,也是解题的入手点!
(2)你是否考虑了问题所有可能的情形?
(3)在每种情形下,你是如何求解的?
(4)对于求得的结果你是否检验了其合理性?如果没有,你从中应该吸取什么教训?
3. (1)探究3一定会用到三角形内角和定理吗?
在三角形内角和定理的证明中,你会哪几种添辅助线的方法?
这些辅助线起到了什么作用?
(2)对于探究3(1),你应用的是算术方法还是方程方法?比较两种方法的优劣.
(3)对于探究3(2),实际上是将数学概念转化为图形和数学式子之后进行运算!
4. (1)你如何将题目中涉及的数学概念(三角形内角的平分线)转化为数学式子并标示在图形上?
(2)根据图形标示,你运用怎样的知识可以找到已知角(包括由数学概念转化为数学式子的角)与未知角之间的联系?
你又应用怎样的数学思想方法实现这种联系?
(3)你能否将问题进行拓展?比如将“内角的平分线”换成“内角的三等分线”会有怎样的结论?四等分线、五等分线、……、n等分线呢?
5. 列举探究题所体现的主要数学思想方法:
探究1:
探究2:
探究3:
探究4:
B
)A.2
B.3
C.5
D.13
探究2 已知一等腰三角形一腰上的中线将此等腰三角形的周长分为7.5,15两部分,求此等腰三角形各边的长.
等腰三角形三边分别为10,10,2.5
探究3 已知△ABC中,∠A= $\frac{2}{3}$∠B= $\frac{1}{2}$∠C.
(1)求∠A、∠B、∠C;
∠A = 40°,∠B = 60°,∠C = 80°
(2)若CD、CE分别是△ABC的高和角平分线,求∠DCE.
10°
探究4 如图,△ABC中,∠A= 40°,点E在线段BC的延长线上,∠ABC的平分线和∠ACE的平分线相交于D,求∠D.
20°

经典题组·新解读
1. 已知三角形两边的长a、b(a>b),求第三边x的取值范围是一个常见题型,它直接考查了
三角形三边关系定理
;其一般解法是
a - b
<x<a + b
. 探究1只是在此基础上的进一步延伸.2. (1)对于探究2你做的第一步工作是什么?
温馨提示:根据题意画出图形既是解题的基础,也是解题的入手点!
根据题意画出图形
(2)你是否考虑了问题所有可能的情形?
考虑了,等腰三角形一腰上的中线将等腰三角形周长分为两部分,有两种情况:腰长与腰长一半的和是7.5,底边长与腰长一半的和是15;或者腰长与腰长一半的和是15,底边长与腰长一半的和是7.5
(3)在每种情形下,你是如何求解的?
设腰长为2x,底边长为y。第一种情况:$\begin{cases}2x + x = 7.5\\x + y = 15\end{cases}$,解得$\begin{cases}x = 2.5\\y = 12.5\end{cases}$,此时三边长为5,5,12.5,因为5 + 5<12.5,不满足三角形三边关系,舍去。第二种情况:$\begin{cases}2x + x = 15\\x + y = 7.5\end{cases}$,解得$\begin{cases}x = 5\\y = 2.5\end{cases}$,此时三边长为10,10,2.5,满足三角形三边关系
(4)对于求得的结果你是否检验了其合理性?如果没有,你从中应该吸取什么教训?
检验了,若不检验可能会得到不符合三角形三边关系的结果,所以以后解题要检验结果是否符合相关定理
3. (1)探究3一定会用到三角形内角和定理吗?
一定会用到三角形内角和定理
在三角形内角和定理的证明中,你会哪几种添辅助线的方法?
这些辅助线起到了什么作用?
添辅助线方法:过A作EF// BC(内错角相等,把三个内角移到一起);延长BC到D,过C作CE// AB(同位角、内错角相等,把三个内角移到一起)等。这些辅助线起到了将三角形三个内角转化到一个平角或同旁内角互补的关系,从而证明三角形内角和为180°
(2)对于探究3(1),你应用的是算术方法还是方程方法?比较两种方法的优劣.
方程方法。算术方法需要较强的逻辑推理和比例运算能力,对于复杂角度关系较难;方程方法通过设未知数,根据角度关系列方程,更直观、简洁,易于理解和求解
(3)对于探究3(2),实际上是将数学概念转化为图形和数学式子之后进行运算!
4. (1)你如何将题目中涉及的数学概念(三角形内角的平分线)转化为数学式子并标示在图形上?
∠ABD=∠DBC=$\frac{1}{2}$∠ABC,∠ACD = ∠DCE=$\frac{1}{2}$∠ACE,在图上分别标示
(2)根据图形标示,你运用怎样的知识可以找到已知角(包括由数学概念转化为数学式子的角)与未知角之间的联系?
运用三角形外角性质(∠ACE=∠A+∠ABC,∠DCE=∠D+∠DBC)找到联系
.你又应用怎样的数学思想方法实现这种联系?
应用等量代换的数学思想方法实现联系
.(3)你能否将问题进行拓展?比如将“内角的平分线”换成“内角的三等分线”会有怎样的结论?四等分线、五等分线、……、n等分线呢?
若换成三等分线,∠D=$\frac{1}{3}$∠A;四等分线,∠D=$\frac{1}{4}$∠A;n等分线,∠D=$\frac{1}{n}$∠A
5. 列举探究题所体现的主要数学思想方法:
探究1:
三角形三边关系思想
探究2:
分类讨论思想、方程思想
探究3:
方程思想、转化思想(利用内角和定理转化角度关系)
探究4:
转化思想(利用外角性质和角平分线性质转化角度关系)、方程思想(通过设未知数找角度关系)
答案:
1. 三角形三边关系定理;$a - b$;$a + b$
2. (1)根据题意画出图形。
(2)考虑了,等腰三角形一腰上的中线将等腰三角形周长分为两部分,有两种情况:腰长与腰长一半的和是$7.5$,底边长与腰长一半的和是$15$;或者腰长与腰长一半的和是$15$,底边长与腰长一半的和是$7.5$。
(3)设腰长为$2x$,底边长为$y$。
第一种情况:$\begin{cases}2x + x = 7.5\\x + y = 15\end{cases}$,解得$\begin{cases}x = 2.5\\y = 12.5\end{cases}$,此时三边长为$5$,$5$,$12.5$,因为$5 + 5\lt12.5$,不满足三角形三边关系,舍去。
第二种情况:$\begin{cases}2x + x = 15\\x + y = 7.5\end{cases}$,解得$\begin{cases}x = 5\\y = 2.5\end{cases}$,此时三边长为$10$,$10$,$2.5$,满足三角形三边关系。
(4)检验了,若不检验可能会得到不符合三角形三边关系的结果,所以以后解题要检验结果是否符合相关定理。
3. (1)一定会用到三角形内角和定理。
添辅助线方法:过$A$作$EF// BC$(内错角相等,把三个内角移到一起);延长$BC$到$D$,过$C$作$CE// AB$(同位角、内错角相等,把三个内角移到一起)等。这些辅助线起到了将三角形三个内角转化到一个平角或同旁内角互补的关系,从而证明三角形内角和为$180^{\circ}$。
(2)方程方法。算术方法需要较强的逻辑推理和比例运算能力,对于复杂角度关系较难;方程方法通过设未知数,根据角度关系列方程,更直观、简洁,易于理解和求解。
4. (1)$\angle ABD=\angle DBC=\frac{1}{2}\angle ABC$,$\angle ACD = \angle DCE=\frac{1}{2}\angle ACE$,在图上分别标示。
(2)运用三角形外角性质($\angle ACE=\angle A+\angle ABC$,$\angle DCE=\angle D+\angle DBC$)找到联系。应用等量代换的数学思想方法实现联系。
(3)若换成三等分线,$\angle D=\frac{1}{3}\angle A$;四等分线,$\angle D=\frac{1}{4}\angle A$;$n$等分线,$\angle D=\frac{1}{n}\angle A$。
5. 探究1:三角形三边关系思想。
探究2:分类讨论思想、方程思想。
探究3:方程思想、转化思想(利用内角和定理转化角度关系)。
探究4:转化思想(利用外角性质和角平分线性质转化角度关系)、方程思想(通过设未知数找角度关系)。
探究1答案:B。
探究2答案:等腰三角形三边分别为$10$,$10$,$2.5$。
探究3:
(1) 解:设$\angle A = x$,则$\angle B=\frac{3}{2}x$,$\angle C = 2x$。
因为$\angle A+\angle B+\angle C = 180^{\circ}$,所以$x+\frac{3}{2}x + 2x=180^{\circ}$,
$\frac{2x + 3x+4x}{2}=180^{\circ}$,$\frac{9x}{2}=180^{\circ}$,$x = 40^{\circ}$。
所以$\angle A = 40^{\circ}$,$\angle B = 60^{\circ}$,$\angle C = 80^{\circ}$。
(2) 因为$CE$平分$\angle ACB$,所以$\angle ACE=\frac{1}{2}\angle ACB = 40^{\circ}$。
因为$CD\perp AB$,$\angle A = 40^{\circ}$,所以$\angle ACD = 50^{\circ}$。
所以$\angle DCE=\angle ACD-\angle ACE=10^{\circ}$。
探究4:
解:因为$\angle ACE=\angle A+\angle ABC$,$BD$平分$\angle ABC$,$CD$平分$\angle ACE$。
设$\angle ABC = 2x$,则$\angle ABD=\angle DBC=x$,$\angle ACE=\angle A + 2x$,$\angle ACD=\angle DCE=\frac{1}{2}(\angle A + 2x)=\frac{\angle A}{2}+x$。
又因为$\angle DCE=\angle D+\angle DBC$,即$\frac{\angle A}{2}+x=\angle D + x$,所以$\angle D=\frac{1}{2}\angle A$。
因为$\angle A = 40^{\circ}$,所以$\angle D = 20^{\circ}$。
2. (1)根据题意画出图形。
(2)考虑了,等腰三角形一腰上的中线将等腰三角形周长分为两部分,有两种情况:腰长与腰长一半的和是$7.5$,底边长与腰长一半的和是$15$;或者腰长与腰长一半的和是$15$,底边长与腰长一半的和是$7.5$。
(3)设腰长为$2x$,底边长为$y$。
第一种情况:$\begin{cases}2x + x = 7.5\\x + y = 15\end{cases}$,解得$\begin{cases}x = 2.5\\y = 12.5\end{cases}$,此时三边长为$5$,$5$,$12.5$,因为$5 + 5\lt12.5$,不满足三角形三边关系,舍去。
第二种情况:$\begin{cases}2x + x = 15\\x + y = 7.5\end{cases}$,解得$\begin{cases}x = 5\\y = 2.5\end{cases}$,此时三边长为$10$,$10$,$2.5$,满足三角形三边关系。
(4)检验了,若不检验可能会得到不符合三角形三边关系的结果,所以以后解题要检验结果是否符合相关定理。
3. (1)一定会用到三角形内角和定理。
添辅助线方法:过$A$作$EF// BC$(内错角相等,把三个内角移到一起);延长$BC$到$D$,过$C$作$CE// AB$(同位角、内错角相等,把三个内角移到一起)等。这些辅助线起到了将三角形三个内角转化到一个平角或同旁内角互补的关系,从而证明三角形内角和为$180^{\circ}$。
(2)方程方法。算术方法需要较强的逻辑推理和比例运算能力,对于复杂角度关系较难;方程方法通过设未知数,根据角度关系列方程,更直观、简洁,易于理解和求解。
4. (1)$\angle ABD=\angle DBC=\frac{1}{2}\angle ABC$,$\angle ACD = \angle DCE=\frac{1}{2}\angle ACE$,在图上分别标示。
(2)运用三角形外角性质($\angle ACE=\angle A+\angle ABC$,$\angle DCE=\angle D+\angle DBC$)找到联系。应用等量代换的数学思想方法实现联系。
(3)若换成三等分线,$\angle D=\frac{1}{3}\angle A$;四等分线,$\angle D=\frac{1}{4}\angle A$;$n$等分线,$\angle D=\frac{1}{n}\angle A$。
5. 探究1:三角形三边关系思想。
探究2:分类讨论思想、方程思想。
探究3:方程思想、转化思想(利用内角和定理转化角度关系)。
探究4:转化思想(利用外角性质和角平分线性质转化角度关系)、方程思想(通过设未知数找角度关系)。
探究1答案:B。
探究2答案:等腰三角形三边分别为$10$,$10$,$2.5$。
探究3:
(1) 解:设$\angle A = x$,则$\angle B=\frac{3}{2}x$,$\angle C = 2x$。
因为$\angle A+\angle B+\angle C = 180^{\circ}$,所以$x+\frac{3}{2}x + 2x=180^{\circ}$,
$\frac{2x + 3x+4x}{2}=180^{\circ}$,$\frac{9x}{2}=180^{\circ}$,$x = 40^{\circ}$。
所以$\angle A = 40^{\circ}$,$\angle B = 60^{\circ}$,$\angle C = 80^{\circ}$。
(2) 因为$CE$平分$\angle ACB$,所以$\angle ACE=\frac{1}{2}\angle ACB = 40^{\circ}$。
因为$CD\perp AB$,$\angle A = 40^{\circ}$,所以$\angle ACD = 50^{\circ}$。
所以$\angle DCE=\angle ACD-\angle ACE=10^{\circ}$。
探究4:
解:因为$\angle ACE=\angle A+\angle ABC$,$BD$平分$\angle ABC$,$CD$平分$\angle ACE$。
设$\angle ABC = 2x$,则$\angle ABD=\angle DBC=x$,$\angle ACE=\angle A + 2x$,$\angle ACD=\angle DCE=\frac{1}{2}(\angle A + 2x)=\frac{\angle A}{2}+x$。
又因为$\angle DCE=\angle D+\angle DBC$,即$\frac{\angle A}{2}+x=\angle D + x$,所以$\angle D=\frac{1}{2}\angle A$。
因为$\angle A = 40^{\circ}$,所以$\angle D = 20^{\circ}$。
查看更多完整答案,请扫码查看


