《2025年学力水平快乐假期快乐暑假七年级数学北师大版北京教育出版社》

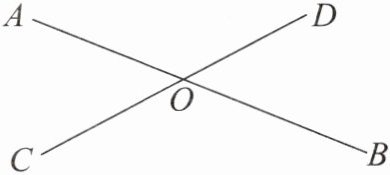
3. 如图,∠AOC= 50°,则这个角的对顶角是∠BOD,它的度数是50°；这个角的邻补角是∠AOD和∠BOC,它的度数是130°。

答案： $\angle BOD$，$50^{\circ}$；$\angle AOD$和$\angle BOC$，$130^{\circ}$。

4. 如图,两组平行线相交,可产生多组相等的角。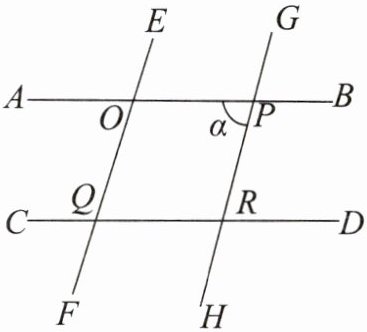
(1)在图中标出与∠α相等的角,并说明它们相等的理由。
(2)图中共有16个小于平角的角,如果知道其中一个角的度数是α°,那么其他15个角的度数分别是$\alpha^{\circ},\alpha^{\circ},\alpha^{\circ},(180 - \alpha)^{\circ},(180 - \alpha)^{\circ},\cdots,(180 - \alpha)^{\circ}$（$3$个$\alpha^{\circ}$，$12$个$(180 - \alpha)^{\circ}$）。

答案： 【解析】：
(1) 与$\angle\alpha$相等的角有$\angle EOP$、$\angle CQO$、$\angle QRG$。
理由：
$\angle\alpha$与$\angle EOP$是对顶角，根据对顶角相等，所以$\angle\alpha=\angle EOP$。
因为$AB// CD$，$EG$为截线，根据两直线平行，同位角相等，所以$\angle\alpha = \angle CQO$。
因为$EF// GH$，$CD$为截线，根据两直线平行，同位角相等，所以$\angle CQO=\angle QRG$，进而$\angle\alpha=\angle QRG$。
(2) 因为图中两组平行线相交，与$\alpha^{\circ}$相等的角有$3$个（不包含$\alpha^{\circ}$本身），与$\alpha^{\circ}$互补的角有$12$个（和为$180^{\circ}$）。
所以其他$15$个角的度数分别是$\alpha^{\circ},\alpha^{\circ},\alpha^{\circ},(180 - \alpha)^{\circ},(180 - \alpha)^{\circ},\cdots,(180 - \alpha)^{\circ}$（$3$个$\alpha^{\circ}$，$12$个$(180 - \alpha)^{\circ}$）。
【答案】：$\boldsymbol{\alpha^{\circ},\alpha^{\circ},\alpha^{\circ},(180 - \alpha)^{\circ},(180 - \alpha)^{\circ},\cdots,(180 - \alpha)^{\circ}}$（$\boldsymbol{3}$个$\boldsymbol{\alpha^{\circ}}$，$\boldsymbol{12}$个$\boldsymbol{(180 - \alpha)^{\circ}}$）