《2025年学力水平快乐假期快乐暑假七年级数学北师大版北京教育出版社》

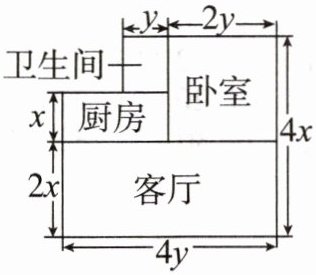
11. 图中标注了有关尺寸(墙体厚度忽略不计,单位：米). 房主计划把卧室以外的地面都铺上地砖,如果他选用地砖的价格是 $ a $ 元/$ \mathrm { m } ^ { 2 } $,那么买地砖至少需要11axy元.

答案： $11axy$

12. 定义一种运算☆,其规则为 $ a ☆ b = \frac { 1 } { a } + \frac { 1 } { b } $,根据这个规则计算 $ 2 ☆ 3 $ 的值是$\frac {5}{6}$.

答案： $\frac {5}{6}$

13. 定义运算 $ a \otimes b = a ( 1 - b ) $,下面给出了关于这种运算的几个结论：① $ 2 \otimes ( - 2 ) = 6 $,② $ a \otimes b = b \otimes a $,③ 若 $ a + b = 0 $,则 $ ( a \otimes a ) + ( b \otimes b ) = 2 a b $,④ 若 $ a \otimes b = 0 $,则 $ a = 0 $. 其中正确结论的序号是①③.

答案： ①③

14. 现有长方形和正方形卡片若干张(如下图).

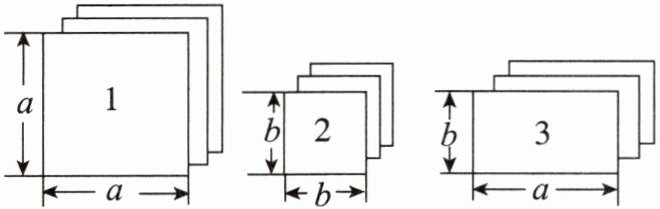
(1) 如果选取 1 号、2 号、3 号卡片分别为 1 张、2 张、3 张,可拼成一个长方形(不重叠无缝隙),请画出这个长方形的草图,并运用拼图前后面积之间的关系说明这个长方形的代数意义.
(2) 小明想用类似方法解释多项式乘法 $ ( a + 3 b ) ( 2 a + b ) = 2 a ^ { 2 } + 7 a b + 3 b ^ { 2 } $,那么需用 2 号卡片______3______张和 3 号卡片______7______张.

答案：

(1)草图如下:

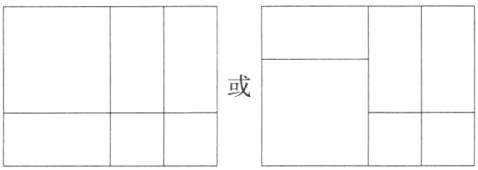
$a^{2}+3ab+2b^{2}=(a+b)(a+2b)$
(2)3 7