《2025年启东中学作业本九年级物理上册苏科版苏北专版》

12. 若甲、乙两物体的比热容之比为2:5,吸收的热量之比为5:1,它们升高的温度相同,则甲、乙两物体的质量之比是(C)
A.1:2
B.2:1
C.25:2
D.2:25

答案： C

13. 在标准大气压下,将质量相同的甲、乙、丙三个金属块加热到相同的温度后,放在上表面平整的冰块上. 经过一段时间后,冰块形状不再变化,状态如图所示. (假设金属块只与冰块发生热传递)则下列说法正确的是(D)
A.最终三个金属块的温度不同
B.最终三个金属块放出的热量相同
C.冰熔化时的温度可能高于0℃
D.丙的比热容一定大于甲、乙的比热容

答案： D

14. 将质量相等、初温相同的水和煤油分别倒入两个完全一样的试管中,然后将这两个试管同时放入温度较高的热水中,如图所示,经过足够长的时间以后,试管中的水和煤油从热水中吸收的热量分别为$Q_1、$$Q_2,$温度升高值分别为$Δt_1、$$Δt_2,$则(已知c水 ＞ c煤油)(C)
$A. Q_1 = Q_2,Δt_1 ＞ Δt_2$
$B. Q_1 = Q_2,Δt_1 = Δt_2$
$C. Q_1 ＞ Q_2,Δt_1 = Δt_2$
$D. Q_1 ＜ Q_2,Δt_1 ＞ Δt_2$

答案： C

15. 在标准大气压下,质量为2kg、初温为20℃的水吸收了$7.56×10^5J$的热量,那么水温升高了多少摄氏度? [c水$ = 4.2×10^3J/(kg·℃)]$

答案： 解: 由 $Q_{吸}=cm\Delta t$ 得 $\Delta t=\frac{Q_{吸}}{c_{水}m}=\frac{7.56×10^{5}J}{4.2×10^{3}J/(kg\cdot^{\circ}C)×2kg}=90^{\circ}C$, $t=t_{0}+\Delta t=20^{\circ}C + 90^{\circ}C=110^{\circ}C$. 因为在标准大气压下, 水的沸点为 $100^{\circ}C$, 所以水的温度升高到 $100^{\circ}C$ 将不再上升, 因此水温升高了 $100^{\circ}C - 20^{\circ}C=80^{\circ}C$.

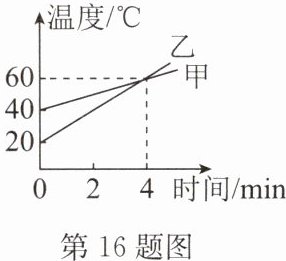
16. 甲、乙两物体的质量之比为4:1,用两个相同的酒精灯分别给它们加热(酒精燃烧放出的热量全部被甲和乙吸收),如图所示为甲、乙两物体的温度随时间的变化图像,若甲的比热容为$2.1×10^3J/(kg·℃),$则:
(1)经过4min甲、乙升高的温度之比为多少?
(2)乙的比热容为多少?

答案： 解:
(1) 经过 4min 甲、乙升高的温度之比 $\Delta t_{甲}:\Delta t_{乙}=20^{\circ}C:40^{\circ}C=1:2$.
(2) 4min 内甲、乙吸收的热量相等, 根据 $Q_{吸}=cm\Delta t$, 得 $c_{甲}m_{甲}\Delta t_{甲}=c_{乙}m_{乙}\Delta t_{乙}$, $c_{乙}=c_{甲}×\frac{m_{甲}}{m_{乙}}×\frac{\Delta t_{甲}}{\Delta t_{乙}}=2.1×10^{3}J/(kg\cdot^{\circ}C)×\frac{4}{1}×\frac{1}{2}=4.2×10^{3}J/(kg\cdot^{\circ}C)$.

17. 将一杯热水倒入盛有冷水的容器中,冷水的温度升高了10℃,再向容器内倒入一杯相同质量和温度的热水,容器中的水温又升高了6℃. 如果继续向容器中倒入一杯同样的热水,则容器中的水温会升高(B)
A.5℃
B.4℃
C.3℃
D.2℃

答案： B 【点拨】设热水和冷水的温度差为 $t$, 质量为 $m_{0}$ 的一杯热水倒入盛有质量为 $m$ 的冷水的容器中, 使得冷水温度升高了 $10^{\circ}C$, 由 $Q_{吸}=Q_{放}$, 得 $cm_{0}(t - 10^{\circ}C)=cm×10^{\circ}C$, ① 又向容器中倒入一杯同质量、同温度的热水, 水温又上升了 $6^{\circ}C$, 由 $Q_{吸}=Q_{放}$, 得 $cm_{0}(t - 10^{\circ}C - 6^{\circ}C)=c(m + m_{0})×6^{\circ}C$, ② 则 ① - ② 得 $6^{\circ}C× cm_{0}=10^{\circ}C× cm - 6^{\circ}C× cm - 6^{\circ}C× cm_{0}$, 整理, 得 $12^{\circ}C× cm_{0}=4^{\circ}C× cm$, 解得 $m = 3m_{0}$, 代入 ① 式可得, $t = 40^{\circ}C$. 假设我们将全部热水一次性倒入冷水中, 则由热平衡方程可知: $3m_{0}c(40^{\circ}C - \Delta t)=mc\Delta t$, $m = 3m_{0}$, 联立两式解得 $\Delta t = 20^{\circ}C$. $40^{\circ}C - 20^{\circ}C = 20^{\circ}C$, 则倒入第 3 杯热水后, 容器中的水温会上升 $20^{\circ}C - 10^{\circ}C - 6^{\circ}C = 4^{\circ}C$.