《2025年春如金卷课时作业AB本八年级数学上册北师大版》

A. 下面关于公理和定理的联系说法不正确的是（B）
A. 公理和定理都是真命题
B. 公理就是定理，定理也是公理
C. 公理和定理都可以作为推理论证的依据
D. 公理的正确性不需证明，定理的正确性需证明

答案： B

B. 下列所学过的真命题中，是公理的是（B）
A. 对顶角相等
B. 同位角相等，两直线平行
C. 三角形两边之和大于第三边
D. 同角的余角相等

答案： B

C. “同角或等角的补角相等”是（C）
A. 定义
B. 公理
C. 定理
D. 假命题

答案： C

证明：$\because AB⊥EF$，$CD⊥EF$，
$\therefore$ ∠ABD=∠CDF$=90^{\circ}$，
$\therefore AB// CD$。

答案： ∠ABD=∠CDF

1. 下列说法正确的是（B）
A. 真命题都可以作为定理
B. 公理不需要证明
C. 定理不一定都要证明
D. 证明只能根据定义、公理进行

答案： B

2. 下列命题不是公理(基本事实)的是（C）
A. 两点确定一条直线
B. 同一平面内，过一点有且只有一条直线垂直于已知直线
C. 两条平行线被第三条直线所截，内错角相等
D. 三边分别相等的两个三角形全等

答案： C

3. 命题“对顶角相等”是（D）
A. 角的定义
B. 假命题
C. 公理
D. 定理

答案： D

4. 命题：全等三角形的对应边上的高相等。
（1）写成“如果…，那么…”的形式：如果两条线段是全等三角形对应边上的高，那么这两条线段相等；
（2）根据所给图形写出已知、求证和证明过程。

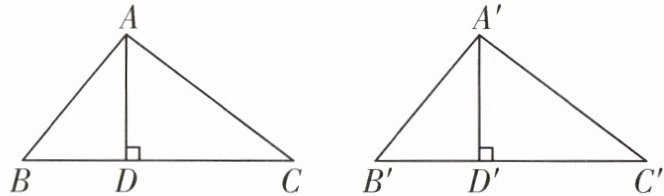
已知:如图,△ABC≌△A'B'C',AD⊥BC,A'D'⊥B'C'。
求证:AD=A'D';
证明:∵△ABC≌△A'B'C',
∴AB=A'B',∠B=∠B',
∵AD⊥BC,A'D'⊥B'C',
∴∠ADB=∠A'D'B'=90°,
在△ABD和△A'B'D'中，$\left\{\begin{array}{l} ∠ADB=∠A'D'B',\\ ∠B=∠B',\\ AB=A'B',\end{array}\right.$
∴△ABD≌△A'B'D'(AAS),
∴AD=A'D'。

答案： 解:
(1)如果两条线段是全等三角形对应边上的高，那么这两条线段相等
(2)已知:如图,△ABC≌△A'B'C',AD⊥BC,A'D'⊥B'C'。
　求证:AD=A'D';
　证明:
∵△ABC≌△A'B'C',
∴AB=A'B',∠B=∠B',
∵AD⊥BC,A'D'⊥B'C',
∴∠ADB=∠A'D'B'=90°,
　在△ABD和△A'B'D'中，$\left\{\begin{array}{l} ∠ADB=∠A'D'B',\\ ∠B=∠B',\\ AB=A'B',\end{array}\right. $
∴△ABD≌△A'B'D'(AAS),
∴AD=A'D'。