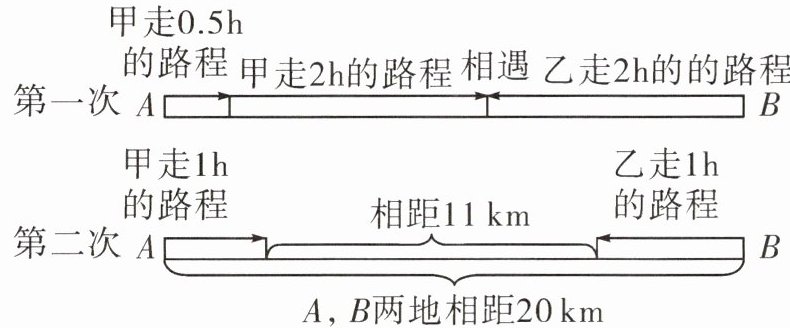
4. 甲乙二人分别从相距20km的A,B两地出发,相向而行。如图是小华绘制的甲乙二人运动两次的情形,设甲的速度是$x$km/h,乙的速度是$y$km/h,根据题意所列的方程组正确的是(
A. $\left\{\begin{array}{l} 2x+2.5y=2,\\ 2x+y=20\end{array}\right. $
B. $\left\{\begin{array}{l} 2.5x+y=20,\\ 2x+y=20\end{array}\right. $
C. $\left\{\begin{array}{l} x+2.5y=20,\\ 2x+y=20\end{array}\right. $
D. $\left\{\begin{array}{l} 2.5x+2y=20,\\ x+y+11=20\end{array}\right. $
D
)
A. $\left\{\begin{array}{l} 2x+2.5y=2,\\ 2x+y=20\end{array}\right. $
B. $\left\{\begin{array}{l} 2.5x+y=20,\\ 2x+y=20\end{array}\right. $
C. $\left\{\begin{array}{l} x+2.5y=20,\\ 2x+y=20\end{array}\right. $
D. $\left\{\begin{array}{l} 2.5x+2y=20,\\ x+y+11=20\end{array}\right. $
答案:
D
5. 8个一样大小的长方形恰好可以拼成一个大的长方形,如图甲所示,若拼成如图乙所示的正方形,中间还留下一个洞,恰好是边长为2cm的小正方形。设一个小长方形的长为$x$cm,宽为$y$cm,则所列二元一次方程组是
$\left\{\begin{array}{l} 3x=5y,\\ 2y=x+2\end{array}\right. $
。
答案:
$\left\{\begin{array}{l} 3x=5y,\\ 2y=x+2\end{array}\right. $
6. 桥长1000m,现有一列匀速行驶的火车从桥上通过,测得火车从车头刚接触桥到完全过桥共用了60s,而整个火车在桥上的时间是40s,求火车的长度和速度。
答案:
解:设火车的速度为x m/s,火车的长度为y m,由题意,得
$\left\{\begin{array}{l} 60x=1000+y,\\ 40x=1000-y,\end{array}\right. $
解得:$\left\{\begin{array}{l} x=20,\\ y=200。\end{array}\right. $
答:火车的速度为20 m/s,火车的长度为200 m。
$\left\{\begin{array}{l} 60x=1000+y,\\ 40x=1000-y,\end{array}\right. $
解得:$\left\{\begin{array}{l} x=20,\\ y=200。\end{array}\right. $
答:火车的速度为20 m/s,火车的长度为200 m。
7. 已知M,N两点在数轴上所表示的数分别为$m$,$n$,且$m$,$n$满足$|m-10|+(n+2)^{2}=0$。
(1)填空:$m=$
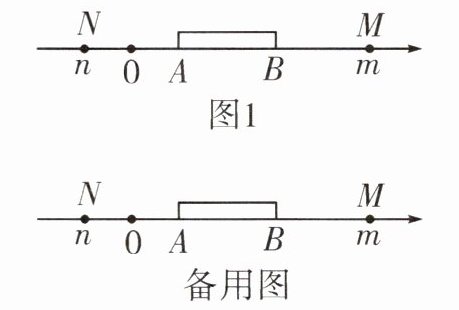
(2)①问题探究:将一根木棒AB如图所示放置在数轴上。将木棒沿数轴左右水平移动,当点A移动到点B时,点B所对应的数为$m$;当点B移动到点A时,点A所对应的数为$n$,由此可得这根木棒的长为
②方法迁移:一天,小明去问爷爷的年龄,爷爷说:“我若是你现在这么大,你还要34年才出生;你若是我现在这么大时,我就116岁啦!”求爷爷的年龄;
(3)在(2)①的条件下,现将木棒AB从某点处切断,切断后左边的木棒以每秒4个单位的速度往左移动,同时右边的木棒以每秒5个单位长度的速度往右移动,是否存在某一时刻,M和N刚好是两段木棒的中点?若存在,求出木棒切断处所表示的数;若不存在,请说明理由。
(1)填空:$m=$
10
,$n=$-2
;(2)①问题探究:将一根木棒AB如图所示放置在数轴上。将木棒沿数轴左右水平移动,当点A移动到点B时,点B所对应的数为$m$;当点B移动到点A时,点A所对应的数为$n$,由此可得这根木棒的长为
4
个单位长度;②方法迁移:一天,小明去问爷爷的年龄,爷爷说:“我若是你现在这么大,你还要34年才出生;你若是我现在这么大时,我就116岁啦!”求爷爷的年龄;
(3)在(2)①的条件下,现将木棒AB从某点处切断,切断后左边的木棒以每秒4个单位的速度往左移动,同时右边的木棒以每秒5个单位长度的速度往右移动,是否存在某一时刻,M和N刚好是两段木棒的中点?若存在,求出木棒切断处所表示的数;若不存在,请说明理由。

答案:
解:
(1)因为$|m-10|+(n+2)^{2}=0,$
所以$m-10=0,n+2=0,$
所以$m=10,n=-2;$
故答案为:10,-2;
(2)①由
(1)知,$MN=10-(-2)=12,$
根据题意可得,$AB=\frac {1}{3}MN=4,$
即这根木棒的长为4个单位长度;
故答案为:4;
②设小明今年x岁,爷爷今年y岁,
根据题意可得方程组为:$\left\{\begin{array}{l} y-x=x+34,\\ y-x=116-y,\end{array}\right. $解得:$\left\{\begin{array}{l} x=12,\\ y=64,\end{array}\right. $
答:爷爷今年64岁;
(3)存在某一时刻,M和N刚好是两段木棒的中点,理由如下:
设木棒切断处所表示的数为x,两段木棒运动的时间为t s,
A表示的数为$-2+4=2$,B表示的数为$10-4=6,$
根据题意得:$\left\{\begin{array}{l} \frac {2-4t+x-4t}{2}=-2,\\ \frac {x+5t+6+5t}{2}=10,\end{array}\right. $
解得$\left\{\begin{array}{l} x=\frac {26}{9},\\ t=\frac {10}{9},\end{array}\right. $
所以木棒切断处所表示的数为$\frac {26}{9}$。
(1)因为$|m-10|+(n+2)^{2}=0,$
所以$m-10=0,n+2=0,$
所以$m=10,n=-2;$
故答案为:10,-2;
(2)①由
(1)知,$MN=10-(-2)=12,$
根据题意可得,$AB=\frac {1}{3}MN=4,$
即这根木棒的长为4个单位长度;
故答案为:4;
②设小明今年x岁,爷爷今年y岁,
根据题意可得方程组为:$\left\{\begin{array}{l} y-x=x+34,\\ y-x=116-y,\end{array}\right. $解得:$\left\{\begin{array}{l} x=12,\\ y=64,\end{array}\right. $
答:爷爷今年64岁;
(3)存在某一时刻,M和N刚好是两段木棒的中点,理由如下:
设木棒切断处所表示的数为x,两段木棒运动的时间为t s,
A表示的数为$-2+4=2$,B表示的数为$10-4=6,$
根据题意得:$\left\{\begin{array}{l} \frac {2-4t+x-4t}{2}=-2,\\ \frac {x+5t+6+5t}{2}=10,\end{array}\right. $
解得$\left\{\begin{array}{l} x=\frac {26}{9},\\ t=\frac {10}{9},\end{array}\right. $
所以木棒切断处所表示的数为$\frac {26}{9}$。
查看更多完整答案,请扫码查看


