《2025年通城学典活页检测九年级数学下册北师大版》

9. (9分)如图，$AB$是⊙O的弦，$C$，$D$为弦 $AB$上的两点，且 $OC = OD$，延长 $OC$，$OD$，分别交⊙O于点 $E$，$F$. 求证：$\overset{\frown}{AE}=\overset{\frown}{BF}$.
　　

答案：
∵ OC = OD，
∴ ∠OCD = ∠ODC.
∵ OA = OB，
∴ ∠A = ∠B.
∵ ∠OCD = ∠A + ∠AOC，∠ODC = ∠B + ∠BOD，
∴ ∠AOC = ∠BOD.
∴ $\overset{\frown}{AE}=\overset{\frown}{BF}$

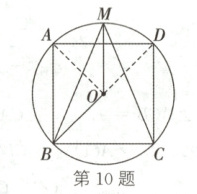
10. (12分)如图，正方形 $ABCD$ 内接于⊙O，$M$为$\overset{\frown}{AD}$的中点，连接 $BM$，$CM$.
(1)求证：$BM = CM$；
(2)连接 $OB$，$OM$，求$\angle BOM$的度数.
　　　　　

答案：

(1)
∵ 四边形 ABCD 是正方形，
∴ AB = CD.
∴ $\overset{\frown}{AB}=\overset{\frown}{CD}$.
∵ M 为 $\overset{\frown}{AD}$ 的中点，
∴ $\overset{\frown}{AM}=\overset{\frown}{DM}$. 又
∵ $\overset{\frown}{BM}=\overset{\frown}{AB}+\overset{\frown}{AM}$，$\overset{\frown}{CM}=\overset{\frown}{CD}+\overset{\frown}{DM}$，
∴ $\overset{\frown}{BM}=\overset{\frown}{CM}$.
∴ BM = CM
(2) 如图，连接 OA，OD.
∵ 四边形 ABCD 是 ⊙O 的内接正方形，
∴ AO⊥BD.
∴ ∠AOB = ∠AOD = 90°.
∵ M 为 $\overset{\frown}{AD}$ 的中点，
∴ ∠AOM = $\frac{1}{2}$∠AOD = 45°.
∴ ∠BOM = ∠AOB + ∠AOM = 90° + 45° = 135°

11. (15分)如图，$AB$是⊙O的直径，$AC = BD$，$\angle COD = 60^{\circ}$. 求证：
(1)$\overset{\frown}{AD}=\overset{\frown}{BC}$；
(2)$\triangle AOC$是等边三角形；
(3)$OC// BD$.
　　　　　　　　　　

答案：
(1)
∵ AC = BD，
∴ $\overset{\frown}{AC}=\overset{\frown}{BD}$.
∴ $\overset{\frown}{AC}+\overset{\frown}{CD}=\overset{\frown}{BD}+\overset{\frown}{CD}$，即 $\overset{\frown}{AD}=\overset{\frown}{BC}$
(2)
∵ AC = BD，
∴ ∠AOC = ∠BOD.
∵ ∠COD = 60°，
∴ ∠AOC + ∠BOD = 180° - ∠COD = 120°.
∴ ∠AOC = ∠BOD = 60°. 又
∵ OC = OA，
∴ △AOC 是等边三角形
(3) 由
(2) 知，∠BOD = ∠AOC = 60°. 又
∵ OD = OB，
∴ △BOD 是等边三角形.
∴ ∠OBD = 60° = ∠AOC.
∴ OC//BD