2025年通城学典活页检测九年级数学下册北师大版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年通城学典活页检测九年级数学下册北师大版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
11. (12分)已知一个等腰直角三角形的斜边长为2x cm,其面积为y cm².
(1)求y关于x的函数表达式,并写出x的取值范围;
(2)列出当x=$\frac{1}{2}$,1,$\frac{3}{2}$,2,$\frac{5}{2}$,3时,y与x的对应值表;
(3)画出y关于x的函数图象.
(1)求y关于x的函数表达式,并写出x的取值范围;
(2)列出当x=$\frac{1}{2}$,1,$\frac{3}{2}$,2,$\frac{5}{2}$,3时,y与x的对应值表;
(3)画出y关于x的函数图象.
答案:
(1)
∵等腰直角三角形的斜边长为2xcm,
∴直角边长为2x·sin45°=$\sqrt{2}$x(cm).
∴y = $\frac{1}{2}$×($\sqrt{2}$x)² = x²(x > 0)
(2) 列表如下:
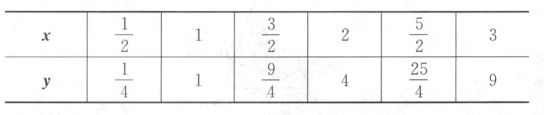
(3) 如图所示

(1)
∵等腰直角三角形的斜边长为2xcm,
∴直角边长为2x·sin45°=$\sqrt{2}$x(cm).
∴y = $\frac{1}{2}$×($\sqrt{2}$x)² = x²(x > 0)
(2) 列表如下:

(3) 如图所示

12. (14分)如图,P是抛物线y=x²上的一点,且在第一象限,点A的坐标是(3,0). 设点P的坐标为(x,y).
(1)求△OPA的面积S关于变量y的函数表达式.
(2)S是x的什么函数?
(3)当S=6时,求点P的坐标.
(4)在y=x²的图象上找一点P',使△OP'A是以OA为底边的等腰三角形.

(1)求△OPA的面积S关于变量y的函数表达式.
(2)S是x的什么函数?
(3)当S=6时,求点P的坐标.
(4)在y=x²的图象上找一点P',使△OP'A是以OA为底边的等腰三角形.

答案:
(1) 由题意,得S = $\frac{1}{2}$×3y = $\frac{3}{2}$y(y > 0)
(2)
∵ y = x²,
∴ S = $\frac{3}{2}$x²(x > 0).
∴ S是x的二次函数
(3)
∵ S = 6,
∴$\begin{cases}6 = \frac{3}{2}y,\\6 = \frac{3}{2}x^{2},\end{cases}$解得$\begin{cases}y = 4,\\x_{1} = 2,x_{2} = - 2.\end{cases}$
∵ x > 0,y > 0,
∴$\begin{cases}y = 4,\\x = 2.\end{cases}$
∴点P的坐标为(2,4)
(4) 由题意,可知OP' = P'A.
∴点P'在OA的垂直平分线上.
∴点P'的横坐标为$\frac{0 + 3}{2} = \frac{3}{2}$.当x = $\frac{3}{2}$时,y = x² = $\frac{9}{4}$.
∴点P'的坐标为($\frac{3}{2}$,$\frac{9}{4}$)
(1) 由题意,得S = $\frac{1}{2}$×3y = $\frac{3}{2}$y(y > 0)
(2)
∵ y = x²,
∴ S = $\frac{3}{2}$x²(x > 0).
∴ S是x的二次函数
(3)
∵ S = 6,
∴$\begin{cases}6 = \frac{3}{2}y,\\6 = \frac{3}{2}x^{2},\end{cases}$解得$\begin{cases}y = 4,\\x_{1} = 2,x_{2} = - 2.\end{cases}$
∵ x > 0,y > 0,
∴$\begin{cases}y = 4,\\x = 2.\end{cases}$
∴点P的坐标为(2,4)
(4) 由题意,可知OP' = P'A.
∴点P'在OA的垂直平分线上.
∴点P'的横坐标为$\frac{0 + 3}{2} = \frac{3}{2}$.当x = $\frac{3}{2}$时,y = x² = $\frac{9}{4}$.
∴点P'的坐标为($\frac{3}{2}$,$\frac{9}{4}$)
查看更多完整答案,请扫码查看


