2025年通城学典活页检测九年级数学下册北师大版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年通城学典活页检测九年级数学下册北师大版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
8. (12分)某片草地的A,B两处分别拴了一只羊和一匹马,其中拴羊的绳长为7 m,拴马的绳长为4 m,且AB = 9 m. 如图,请你在图中画出羊和马都可以吃到草的区域.


答案:
如图,图中涂色部分即为所求
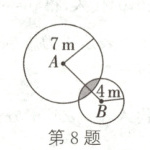
如图,图中涂色部分即为所求

9. (12分)如图,BD,CE是△ABC的高,M为BC的中点. 求证:点B,C,D,E在以点M为圆心的同一个圆上.


答案:
如图,连接$ME$,$MD$.$\because BD$,$CE$是$\triangle ABC$的高,$\therefore \angle BDC=\angle BEC = 90^{\circ}$.$\because M$为$BC$的中点,$\therefore MD=\frac{1}{2}BC$,$ME=\frac{1}{2}BC$,$MB = MC=\frac{1}{2}BC$.$\therefore MB = MC = MD = ME$.$\therefore$点$B$,$C$,$D$,$E$在以点$M$为圆心的同一个圆上
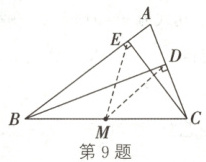
如图,连接$ME$,$MD$.$\because BD$,$CE$是$\triangle ABC$的高,$\therefore \angle BDC=\angle BEC = 90^{\circ}$.$\because M$为$BC$的中点,$\therefore MD=\frac{1}{2}BC$,$ME=\frac{1}{2}BC$,$MB = MC=\frac{1}{2}BC$.$\therefore MB = MC = MD = ME$.$\therefore$点$B$,$C$,$D$,$E$在以点$M$为圆心的同一个圆上

10. (14分)小明在求同一平面直角坐标系内两点间的距离时发现,对于平面直角坐标系内任意两点$P_1(x_1,y_1)$,$P_2(x_2,y_2)$,可通过构造直角三角形,利用勾股定理得到结论:$P_1P_2=\sqrt{(x_2 - x_1)^2+(y_2 - y_1)^2}$;他还证明了线段$P_1P_2$的中点$P(x,y)$的坐标公式为$x=\frac{x_1 + x_2}{2}$,$y=\frac{y_1 + y_2}{2}$.
请利用上面的信息,解决下面的问题:
如图,在平面直角坐标系中,已知点A(8,0),B(0,6),⊙M经过原点O及点A,B(AB为直径).
(1)求⊙M的半径及圆心M的坐标;
(2)若点C的坐标为(1,7),判断点C与⊙M的位置关系,并说明理由.

请利用上面的信息,解决下面的问题:
如图,在平面直角坐标系中,已知点A(8,0),B(0,6),⊙M经过原点O及点A,B(AB为直径).
(1)求⊙M的半径及圆心M的坐标;
(2)若点C的坐标为(1,7),判断点C与⊙M的位置关系,并说明理由.

答案:
(1)$\because$点$A$的坐标为$(8,0)$,点$B$的坐标为$(0,6)$,$\therefore AB=\sqrt{(0 - 8)^{2}+(6 - 0)^{2}} = 10$.$\therefore \odot M$的半径为$5$.$\because$圆心$M$的横坐标为$\frac{8 + 0}{2}=4$,纵坐标为$\frac{0 + 6}{2}=3$,$\therefore$圆心$M$的坐标为$(4,3)$
(2)点$C$在$\odot M$上 理由:$\because$点$C$的坐标为$(1,7)$,点$M$的坐标为$(4,3)$,$\therefore CM=\sqrt{(4 - 1)^{2}+(3 - 7)^{2}} = 5$.$\because \odot M$的半径为$5$,$\therefore$点$C$在$\odot M$上.
(1)$\because$点$A$的坐标为$(8,0)$,点$B$的坐标为$(0,6)$,$\therefore AB=\sqrt{(0 - 8)^{2}+(6 - 0)^{2}} = 10$.$\therefore \odot M$的半径为$5$.$\because$圆心$M$的横坐标为$\frac{8 + 0}{2}=4$,纵坐标为$\frac{0 + 6}{2}=3$,$\therefore$圆心$M$的坐标为$(4,3)$
(2)点$C$在$\odot M$上 理由:$\because$点$C$的坐标为$(1,7)$,点$M$的坐标为$(4,3)$,$\therefore CM=\sqrt{(4 - 1)^{2}+(3 - 7)^{2}} = 5$.$\because \odot M$的半径为$5$,$\therefore$点$C$在$\odot M$上.
查看更多完整答案,请扫码查看


