2025年通城学典活页检测九年级数学下册北师大版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年通城学典活页检测九年级数学下册北师大版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
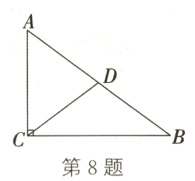
8. (14分)如图,在Rt△ABC中,∠ACB = 90°,D为AB的中点,CD = 5,AC = 6.求tan A,tan B的值.

答案:
∵∠ACB = 90°,D为AB的中点,CD = 5,
∴AB = 2CD = 10.在Rt△ABC中,由勾股定理,得BC = $\sqrt{AB^{2}-AC^{2}}=\sqrt{10^{2}-6^{2}} = 8$.
∴tanA = $\frac{BC}{AC}=\frac{8}{6}=\frac{4}{3}$,tanB = $\frac{AC}{BC}=\frac{6}{8}=\frac{3}{4}$
∵∠ACB = 90°,D为AB的中点,CD = 5,
∴AB = 2CD = 10.在Rt△ABC中,由勾股定理,得BC = $\sqrt{AB^{2}-AC^{2}}=\sqrt{10^{2}-6^{2}} = 8$.
∴tanA = $\frac{BC}{AC}=\frac{8}{6}=\frac{4}{3}$,tanB = $\frac{AC}{BC}=\frac{6}{8}=\frac{3}{4}$
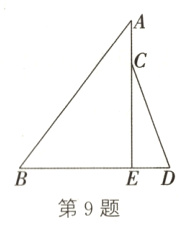
9. (15分)如图,方方和圆圆分别将两根木棒AB,CD斜靠在竖直的墙AE(厚度忽略不计)上,其中AB = 10 dm,CD = 6 dm,BE = 6 dm,DE = 2 dm.你能判断谁的木棒更陡吗? 请说明理由.

答案:
圆圆的木棒CD更陡 理由:由题意,得AE⊥BD.在Rt△ABE中,由勾股定理,得AE = $\sqrt{AB^{2}-BE^{2}}=\sqrt{10^{2}-6^{2}} = 8(dm)$.
∴AB的坡度为$\frac{AE}{BE}=\frac{8}{6}=\frac{4}{3}$.在Rt△CDE中,由勾股定理,得CE = $\sqrt{CD^{2}-DE^{2}}=\sqrt{6^{2}-2^{2}} = 4\sqrt{2}(dm)$.
∴CD的坡度为$\frac{CE}{DE}=\frac{4\sqrt{2}}{2}=2\sqrt{2}$.
∵$\frac{4}{3}$<2$\sqrt{2}$,
∴圆圆的木棒CD更陡.
∴AB的坡度为$\frac{AE}{BE}=\frac{8}{6}=\frac{4}{3}$.在Rt△CDE中,由勾股定理,得CE = $\sqrt{CD^{2}-DE^{2}}=\sqrt{6^{2}-2^{2}} = 4\sqrt{2}(dm)$.
∴CD的坡度为$\frac{CE}{DE}=\frac{4\sqrt{2}}{2}=2\sqrt{2}$.
∵$\frac{4}{3}$<2$\sqrt{2}$,
∴圆圆的木棒CD更陡.
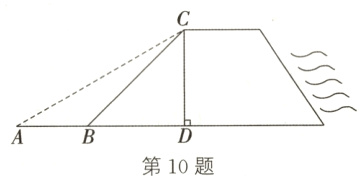
10. (15分)如图所示为某水库大坝的横截面,坝高CD = 20 m,背水坡BC的坡度为1 : 1.为了对水库大坝进行升级加固,降低背水坡的倾斜程度,工程队准备把背水坡的坡度改为1 : $\sqrt{3}$.求背水坡新起点A与原起点B之间的距离.

答案:
在Rt△BCD中,
∵BC的坡度为1:1,
∴$\frac{CD}{BD}=1$.
∴BD = CD = 20m.在Rt△ACD中,
∵AC的坡度为1:$\sqrt{3}$,
∴$\frac{CD}{AD}=\frac{1}{\sqrt{3}}$.
∴AD = $\sqrt{3}$CD = 20$\sqrt{3}$m.
∴AB = AD - BD = (20$\sqrt{3}$ - 20)m.
∴背水坡新起点A与原起点B之间的距离为(20$\sqrt{3}$ - 20)m
∵BC的坡度为1:1,
∴$\frac{CD}{BD}=1$.
∴BD = CD = 20m.在Rt△ACD中,
∵AC的坡度为1:$\sqrt{3}$,
∴$\frac{CD}{AD}=\frac{1}{\sqrt{3}}$.
∴AD = $\sqrt{3}$CD = 20$\sqrt{3}$m.
∴AB = AD - BD = (20$\sqrt{3}$ - 20)m.
∴背水坡新起点A与原起点B之间的距离为(20$\sqrt{3}$ - 20)m
查看更多完整答案,请扫码查看


