《2025年通城学典活页检测九年级数学下册北师大版》

7. (14分)为了进一步改善居住环境，提高居民生活的幸福指数，某小区物业公司决定对小区环境进行优化改造. 如图，AB表示该小区一段长为20 m的斜坡，坡角∠BAD = 30°，BD⊥AD于点D. 为方便通行，在不改变斜坡高度的情况下，把坡角降为15°. 求：
(1) 该斜坡的高度BD；
(2) 斜坡新起点C与原起点A之间的距离.
　　　　　　

答案：
(1) 在Rt△ABD中，
∵∠BAD = 30°，AB = 20 m，
∴BD = AB·sin∠BAD = 20×sin 30° = 20×1/2 = 10(m).
∴该斜坡的高度BD为10 m
(2)
∵∠BAD = 30°，∠BCA = 15°，
∴∠CBA = ∠BAD - ∠BCA = 30° - 15° = 15°.
∴AC = AB = 20 m.
∴斜坡新起点C与原起点A之间的距离为20 m

8. (16分)(安徽中考)如图，为了测量河对岸A，B两点之间的距离，数学兴趣小组在河岸南侧选定观测点C，测得点A，B均在点C的北偏东37°方向上，沿正东方向行走90米至观测点D，测得点A在点D的正北方向上，点B在点D的北偏西53°方向上. 求A，B两点之间的距离(参考数据：sin 37°≈0.60，cos 37°≈0.80，tan 37°≈0.75).
　　　　

答案：
∵CE//AD，
∴∠A = ∠ECA = 37°.
∴∠CBD = ∠A + ∠ADB = 37° + 53° = 90°.
∴BD⊥AC. 在Rt△BCD中，
∵∠BDC = 90° - 53° = 37°，CD = 90米，cos∠BDC = BD/CD，
∴BD = CD·cos 37°≈90×0.80 = 72(米). 在Rt△ABD中，
∵∠A = 37°，BD = 72米，tan A = BD/AB，
∴AB = BD/tan 37°≈72/0.75 = 96(米).
∴A，B两点之间的距离约为96米

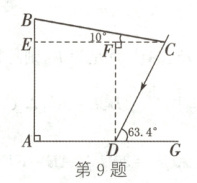
9. (16分)(达州中考)某老年活动中心欲在一房前3 m高的前墙(AB)上安装一遮阳篷BC，使正午时刻房前能有2 m宽的阴影处(AD)以供纳凉. 假设此地某日正午时刻太阳光与水平地面的夹角为63.4°，遮阳篷BC与水平面的夹角为10°. 如图所示为侧面的示意图，请你求出遮阳篷BC的长度(结果精确到0.1 m，参考数据：sin 10°≈0.17，cos 10°≈0.98，tan 10°≈0.18，sin 63.4°≈0.89，cos 63.4°≈0.45，tan 63.4°≈2.00).
　

答案：
如图，过点D作DF⊥CE于点F.
∵EC//AD，∠CDG = 63.4°，
∴∠FCD = ∠CDG = 63.4°. 在Rt△FCD中，
∵tan∠FCD = DF/CF = tan 63.4°≈2.00，
∴DF/CF = 2.
∴DF = 2CF. 设CF = x m，则DF = 2x m，易得四边形ADFE是矩形.
∴AE = DF = 2x m，EF = AD = 2 m.
∴BE = (3 - 2x) m，CE = (2 + x) m. 在Rt△BCE中，
∵tan∠BCE = BE/CE = tan 10°≈0.18，
∴0.18 = (3 - 2x)/(2 + x)，解得x≈1.21.
∴BE = 3 - 2×1.21 = 0.58(m). 在Rt△BCE中，
∵sin∠BCE = BE/BC，
∴BC = BE/sin∠BCE = BE/sin 10°≈0.58/0.17≈3.4(m).
∴遮阳篷BC的长度约为3.4