2025年通城学典活页检测九年级数学下册北师大版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年通城学典活页检测九年级数学下册北师大版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
10. (12分)已知一个正方形的周长为$C$,面积为$S$.
(1) 求$S$关于$C$的函数表达式,并画出图象;
(2) 根据图象,求出当$S = 1$时,正方形的周长.
(1) 求$S$关于$C$的函数表达式,并画出图象;
(2) 根据图象,求出当$S = 1$时,正方形的周长.
答案:
(1) 由题意,得S = ($\frac{C}{4}$)² = $\frac{C²}{16}$(C>0). 列表如下:

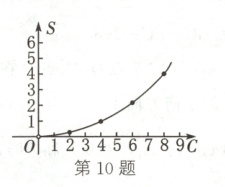
画出图象如图所示
(2) 由图象,可知当S = 1时,C = 4,即正方形的周长是4
(1) 由题意,得S = ($\frac{C}{4}$)² = $\frac{C²}{16}$(C>0). 列表如下:

画出图象如图所示
(2) 由图象,可知当S = 1时,C = 4,即正方形的周长是4

11. (12分)已知函数$y = (m + 2)x^{m^{2}+m - 4}$是关于$x$的二次函数.
(1) 求$m$的值.
(2) 当$m$为何值时,二次函数的图象有最高点?求出这个最高点的坐标,并写出当$x$在什么范围内时,$y$随$x$的增大而增大.
(1) 求$m$的值.
(2) 当$m$为何值时,二次函数的图象有最高点?求出这个最高点的坐标,并写出当$x$在什么范围内时,$y$随$x$的增大而增大.
答案:
(1) 由题意,得m² + m - 4 = 2,且m + 2 ≠ 0,解得m₁ = 2,m₂ = - 3
(2) 若二次函数的图象有最高点,则二次函数的图象开口向下.
∴ m + 2 < 0,即m < - 2.
∴ 当m = - 3时,y = - x²,二次函数的图象有最高点,最高点为二次函数的图象的顶点,其坐标为(0,0). 当x < 0时,y随x的增大而增大
(1) 由题意,得m² + m - 4 = 2,且m + 2 ≠ 0,解得m₁ = 2,m₂ = - 3
(2) 若二次函数的图象有最高点,则二次函数的图象开口向下.
∴ m + 2 < 0,即m < - 2.
∴ 当m = - 3时,y = - x²,二次函数的图象有最高点,最高点为二次函数的图象的顶点,其坐标为(0,0). 当x < 0时,y随x的增大而增大
12. (14分)已知抛物线$y = ax^{2}+k$与$y = 3x^{2}$仅位置不同,其顶点坐标是$(0,-2)$.
(1) 写出抛物线$y = ax^{2}+k$对应的函数表达式,并说明该抛物线是由抛物线$y = 3x^{2}$经过怎样的平移变换得到的;
(2) 写出抛物线$y = ax^{2}+k$的开口方向和对称轴;
(3) 写出$y$随$x$的变化而变化的情况;
(4) 若$M(x_{1},y_{1}),N(x_{2},y_{2})$是抛物线$y = ax^{2}+k$上的两点,且$x_{1}<x_{2}<0$,试比较$y_{1}$与$y_{2}$的大小.
(1) 写出抛物线$y = ax^{2}+k$对应的函数表达式,并说明该抛物线是由抛物线$y = 3x^{2}$经过怎样的平移变换得到的;
(2) 写出抛物线$y = ax^{2}+k$的开口方向和对称轴;
(3) 写出$y$随$x$的变化而变化的情况;
(4) 若$M(x_{1},y_{1}),N(x_{2},y_{2})$是抛物线$y = ax^{2}+k$上的两点,且$x_{1}<x_{2}<0$,试比较$y_{1}$与$y_{2}$的大小.
答案:
(1) 由题意,得a = 3,k = - 2.
∴ y = 3x² - 2. 它是由抛物线y = 3x²向下平移2个单位长度得到的
(2) 开口向上,对称轴为y轴
(3) 当x > 0时,y随x的增大而增大;当x < 0时,y随x的增大而减小
(4) 由
(3),可知y₁ > y₂
(1) 由题意,得a = 3,k = - 2.
∴ y = 3x² - 2. 它是由抛物线y = 3x²向下平移2个单位长度得到的
(2) 开口向上,对称轴为y轴
(3) 当x > 0时,y随x的增大而增大;当x < 0时,y随x的增大而减小
(4) 由
(3),可知y₁ > y₂
查看更多完整答案,请扫码查看


