2025年通城学典活页检测九年级数学下册北师大版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年通城学典活页检测九年级数学下册北师大版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
8. (12分)如图,∠ACB = 90°,Rt△ABC的斜边AB在x轴上,斜边上的高CO在y轴上,且OA = 1,OC = 2,求经过A,B,C三点的抛物线对应的函数表达式.


答案:
∵∠AOC=∠ACB = 90°,
∴∠CAO+∠ACO = 90°,∠CAO+∠CBO = 90°.
∴∠ACO=∠CBO. 又
∵∠AOC=∠COB = 90°,
∴△ACO∽△CBO.
∴$\frac{OC}{OB}=\frac{OA}{OC}$.
∴OC²=OB·OA.
∵OA = 1,OC = 2,
∴OB = 4.
∴A(-1,0),B(4,0),C(0,2). 设经过A,B,C三点的抛物线对应的函数表达式为$y = ax^{2}+bx + c$. 将A(-1,0),B(4,0),C(0,2)代入,得$\begin{cases}a - b + c = 0,\\16a + 4b + c = 0,\\c = 2,\end{cases}$解得$\begin{cases}a = -\frac{1}{2},\\b = \frac{3}{2},\\c = 2.\end{cases}$
∴经过A,B,C三点的抛物线对应的函数表达式为$y = -\frac{1}{2}x^{2}+\frac{3}{2}x + 2$
∵∠AOC=∠ACB = 90°,
∴∠CAO+∠ACO = 90°,∠CAO+∠CBO = 90°.
∴∠ACO=∠CBO. 又
∵∠AOC=∠COB = 90°,
∴△ACO∽△CBO.
∴$\frac{OC}{OB}=\frac{OA}{OC}$.
∴OC²=OB·OA.
∵OA = 1,OC = 2,
∴OB = 4.
∴A(-1,0),B(4,0),C(0,2). 设经过A,B,C三点的抛物线对应的函数表达式为$y = ax^{2}+bx + c$. 将A(-1,0),B(4,0),C(0,2)代入,得$\begin{cases}a - b + c = 0,\\16a + 4b + c = 0,\\c = 2,\end{cases}$解得$\begin{cases}a = -\frac{1}{2},\\b = \frac{3}{2},\\c = 2.\end{cases}$
∴经过A,B,C三点的抛物线对应的函数表达式为$y = -\frac{1}{2}x^{2}+\frac{3}{2}x + 2$
9. (16分)有这样一道题:已知二次函数$y = ax^{2}+bx + c$的图象经过点A(1,-4),B(0,-3), ,求证:这个二次函数的图象必经过定点P(-1,0).题中的矩形阴影部分是一个被墨水污染从而无法辨认的条件.
,求证:这个二次函数的图象必经过定点P(-1,0).题中的矩形阴影部分是一个被墨水污染从而无法辨认的条件.
(1) 你能根据题中信息求出这个二次函数的表达式吗?若能,请求出;若不能,请说明理由.
(2) 请你根据已有信息,在原题中添加一个适当的条件,把原题补充完整.
 ,求证:这个二次函数的图象必经过定点P(-1,0).题中的矩形阴影部分是一个被墨水污染从而无法辨认的条件.
,求证:这个二次函数的图象必经过定点P(-1,0).题中的矩形阴影部分是一个被墨水污染从而无法辨认的条件.(1) 你能根据题中信息求出这个二次函数的表达式吗?若能,请求出;若不能,请说明理由.
(2) 请你根据已有信息,在原题中添加一个适当的条件,把原题补充完整.
答案:
(1) 能 把A(1,-4),B(0,-3),P(-1,0)代入$y = ax^{2}+bx + c$,得$\begin{cases}-4 = a + b + c,\\-3 = c,\\0 = a - b + c,\end{cases}$ 解得$\begin{cases}a = 1,\\b = -2,\\c = -3.\end{cases}$
∴这个二次函数的表达式为$y = x^{2}-2x - 3$
(2) 答案不唯一,如该图象的对称轴为直线$x = 1$
(1) 能 把A(1,-4),B(0,-3),P(-1,0)代入$y = ax^{2}+bx + c$,得$\begin{cases}-4 = a + b + c,\\-3 = c,\\0 = a - b + c,\end{cases}$ 解得$\begin{cases}a = 1,\\b = -2,\\c = -3.\end{cases}$
∴这个二次函数的表达式为$y = x^{2}-2x - 3$
(2) 答案不唯一,如该图象的对称轴为直线$x = 1$
10. (16分)(常德中考)如图,抛物线过点O(0,0),A(5,5),且它的对称轴为直线x = 2.
(1) 求此抛物线对应的函数表达式;
(2) 若B是抛物线对称轴上的一点,且点B在第一象限,当△OAB的面积为15时,求点B的坐标.
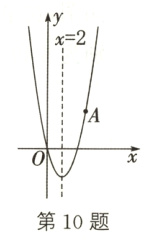
(1) 求此抛物线对应的函数表达式;
(2) 若B是抛物线对称轴上的一点,且点B在第一象限,当△OAB的面积为15时,求点B的坐标.

答案:
(1)
∵抛物线过点O(0,0),A(5,5),且它的对称轴为直线$x = 2$,
∴抛物线与x轴的另一个交点的坐标为(4,0). 设抛物线对应的函数表达式为$y = ax(x - 4)$. 把A(5,5)代入,得$5a = 5$,解得$a = 1$.$\therefore y = x(x - 4)=x^{2}-4x$.
∴此抛物线对应的函数表达式为$y = x^{2}-4x$
(2)
∵B是抛物线对称轴上的一点,且点B在第一象限,
∴设$B(2,m)(m>0)$,设直线OA对应的函数表达式为$y = kx$,则$5k = 5$,解得$k = 1$.
∴直线OA对应的函数表达式为$y = x$. 如图,设直线OA与抛物线对称轴交于点H,则$H(2,2)$.
∴$BH = m - 2$.
∵$S_{\triangle OAB}=S_{\triangle OBH}+S_{\triangle ABH}=15$,
∴$\frac{1}{2}\times(m - 2)\times5 = 15$,解得$m = 8$.
∴点B的坐标为(2,8)
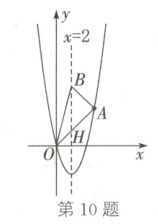
(1)
∵抛物线过点O(0,0),A(5,5),且它的对称轴为直线$x = 2$,
∴抛物线与x轴的另一个交点的坐标为(4,0). 设抛物线对应的函数表达式为$y = ax(x - 4)$. 把A(5,5)代入,得$5a = 5$,解得$a = 1$.$\therefore y = x(x - 4)=x^{2}-4x$.
∴此抛物线对应的函数表达式为$y = x^{2}-4x$
(2)
∵B是抛物线对称轴上的一点,且点B在第一象限,
∴设$B(2,m)(m>0)$,设直线OA对应的函数表达式为$y = kx$,则$5k = 5$,解得$k = 1$.
∴直线OA对应的函数表达式为$y = x$. 如图,设直线OA与抛物线对称轴交于点H,则$H(2,2)$.
∴$BH = m - 2$.
∵$S_{\triangle OAB}=S_{\triangle OBH}+S_{\triangle ABH}=15$,
∴$\frac{1}{2}\times(m - 2)\times5 = 15$,解得$m = 8$.
∴点B的坐标为(2,8)

查看更多完整答案,请扫码查看


