《2025年通城学典活页检测九年级数学下册北师大版》

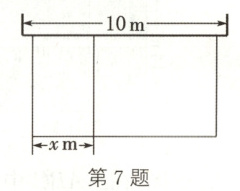
7. (20分)(无锡中考)某农场计划建造一个矩形养殖场，为充分利用现有资源，该矩形养殖场一边靠墙(墙的长度为10m)，另外三边用栅栏围成，中间再用栅栏把它分成面积比为1 : 2的两个小矩形. 已知栅栏的总长度为24m，设最小矩形平行于墙的边的长为xm(如图).
(1) 若矩形养殖场的总面积为36m²，求此时x的值.
(2) 当x的值为多少时，矩形养殖场的总面积最大？最大总面积为多少？

答案： （1）由题意，得$(x + 2x)\cdot\frac{24 - x - 2x}{3}=36$，解得$x_1 = 2$，$x_2 = 6$.当$x = 6$时，$x + 2x = 18＞10$，不符合题意，舍去；当$x = 2$时，$x + 2x = 6＜10$，符合题意.
∴此时$x$的值为2 （2）设矩形养殖场的总面积是$y\mathrm{m}^2$.$\because$墙的长度为10 m，$\therefore0＜x + 2x\leqslant10$，解得$0＜x\leqslant\frac{10}{3}$.由题意，得$y=(x + 2x)\cdot\frac{24 - x - 2x}{3}=-3x^2 + 24x=-3(x - 4)^2 + 48$.$\because - 3＜0$，$\frac{10}{3}＜4$，$\therefore$当$x=\frac{10}{3}$时，$y$取最大值，最大值为$-3\times(\frac{10}{3}-4)^2 + 48=\frac{140}{3}$.$\therefore$当$x=\frac{10}{3}$时，矩形养殖场的总面积最大，最大总面积为$\frac{140}{3}\mathrm{m}^2$

8. (26分)隧道的截面由抛物线和矩形AOBB₁组成，矩形的一边长为12m，另一边长为4m. 建立如图所示的平面直角坐标系，抛物线可以用y = -$\frac{1}{6}x^{2}+bx+c$表示，且抛物线上的点C到墙面OB的距离为3m，到地面OA的距离为$\frac{17}{2}$m.
(1) 求该抛物线对应的函数表达式和拱顶D到地面OA的距离.
(2) 一辆货运汽车载一长方体集装箱后高6m，宽4m，如果隧道内设双向行车道，那么这辆货运汽车能否安全通过？
(3) 在抛物线型拱壁上需要安装两排灯，使它们离地面的高度相等. 如果灯离地面的高度不超过8m，那么两排灯的水平距离最小是多少？
　　　　　

答案： （1）由题意，得点$B$的坐标为$(0,4)$，点$C$的坐标为$(3,\frac{17}{2})$.把$B(0,4)$，$C(3,\frac{17}{2})$分别代入$y = -\frac{1}{6}x^2 + bx + c$，得$\begin{cases}4 = c,\\\frac{17}{2}=-\frac{1}{6}\times3^2 + 3b + c,\end{cases}$解得$\begin{cases}b = 2,\\c = 4.\end{cases}$
∴该抛物线对应的函数表达式为$y = -\frac{1}{6}x^2 + 2x + 4$，即$y = -\frac{1}{6}(x - 6)^2 + 10$.$\therefore$点$D$的坐标为$(6,10)$.$\therefore$拱顶$D$到地面$OA$的距离为10 m （2）由（1），得抛物线的对称轴为直线$x = 6$，且货运汽车的宽为4 m，$\therefore$由题意，得当货运汽车靠中间行驶时，它的最外侧与地面$OA$的交点坐标为$(2,0)$或$(10,0)$.当$x = 2$时，$y = -\frac{1}{6}\times(2 - 6)^2 + 10=\frac{22}{3}$；当$x = 10$时，$y = -\frac{1}{6}\times(10 - 6)^2 + 10=\frac{22}{3}$.$\because\frac{22}{3}＞6$，$\therefore$这辆货运汽车能安全通过 （3）令$y = 8$，则$-\frac{1}{6}(x - 6)^2 + 10 = 8$，解得$x_1 = 6 + 2\sqrt{3}$，$x_2 = 6 - 2\sqrt{3}$.$\because x_1 - x_2 = 4\sqrt{3}$，$\therefore$两排灯的水平距离最小是$4\sqrt{3}\mathrm{m}$