2024年高中必刷题高二数学选择性必修第一册人教B版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2024年高中必刷题高二数学选择性必修第一册人教B版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第5页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
1. [江西宜春 2024 高二月考]已知向量 i,j,k 是一组单位向量,且两两垂直.若 m = 8j + 3k,n = -i + 5j - 4k,则 m·n 的值为 ( )
A.7
B.-20
C.28
D.11
A.7
B.-20
C.28
D.11
答案:
C【解析】向量$i,j,k$是一组单位向量,且两两垂直,所以$|i| = |j| = |k| = 1$且$i\cdot j = j\cdot k = i\cdot k = 0$。因为$m = 8j + 3k$,$n = -i + 5j - 4k$,所以$m\cdot n=(8j + 3k)\cdot(-i + 5j - 4k)=40 - 12 = 28$。故选C。
2. (多选)已知 a,b 为空间中的任意两个非零向量,则下列各式正确的有 ( )
A.a² = |a|²
B.$\frac{a·b}{a²}=\frac{b}{a}$
C.(a·b)² = a²·b²
D.(a - b)² = a² - 2a·b + b²
A.a² = |a|²
B.$\frac{a·b}{a²}=\frac{b}{a}$
C.(a·b)² = a²·b²
D.(a - b)² = a² - 2a·b + b²
答案:
AD【解析】由数量积的性质和运算律可知AD是正确的。
3. [辽宁沈阳东北育才学校 2024 高二期中]如图,正四面体 ABCD 的棱长为 2,点 E,F 分别为棱 AD,BC 的中点,则$\overrightarrow{EF}·\overrightarrow{BA}$的值为 ( )
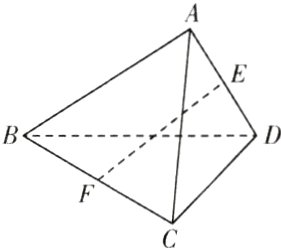
A.4
B.-4
C.-2
D.2

A.4
B.-4
C.-2
D.2
答案:
C【解析】$\because\overrightarrow{EF}=\overrightarrow{EA}+\overrightarrow{AB}+\overrightarrow{BF}=\frac{1}{2}\overrightarrow{DA}+\overrightarrow{AB}+\frac{1}{2}\overrightarrow{BC}$,$\therefore\overrightarrow{EF}\cdot\overrightarrow{BA}=(\frac{1}{2}\overrightarrow{DA}+\overrightarrow{AB}+\frac{1}{2}\overrightarrow{BC})\cdot\overrightarrow{BA}=\frac{1}{2}\overrightarrow{AD}\cdot\overrightarrow{AB}-\overrightarrow{AB}^{2}+\frac{1}{2}\overrightarrow{BC}\cdot\overrightarrow{BA}=\frac{1}{2}\times2^{2}\cos60^{\circ}-2^{2}+\frac{1}{2}\times2^{2}\times\cos60^{\circ}=-2$。故选C。
4. [河北石家庄 2024 高二月考]如图,三棱锥 S - ABC 的棱长均为 a,点 E,F,G 分别是 SA,SC,BC 的中点,则 - a² = ( )

A.2$\overrightarrow{AS}·\overrightarrow{AB}$
B.2$\overrightarrow{FG}·\overrightarrow{SB}$
C.4$\overrightarrow{FG}·\overrightarrow{EF}$
D.4$\overrightarrow{EF}·\overrightarrow{BA}$

A.2$\overrightarrow{AS}·\overrightarrow{AB}$
B.2$\overrightarrow{FG}·\overrightarrow{SB}$
C.4$\overrightarrow{FG}·\overrightarrow{EF}$
D.4$\overrightarrow{EF}·\overrightarrow{BA}$
答案:
D【解析】由题意知三棱锥S - ABC为正四面体。如图所示,

取AC的中点D,连接SD,BD,则$SD\perp AC$,$BD\perp AC$,$SD\cap BD = D$,$SD$,$BD\subset$平面SBD,所以$AC\perp$平面SBD。又$SB\subset$平面SBD,所以$AC\perp SB$,点E,F,G分别是SA,SC,BC的中点,所以$FG// SB$,$EF// AC$,所以$EF\perp FG$,且$EF = FG=\frac{1}{2}a$。所以$2\overrightarrow{AS}\cdot\overrightarrow{AB}=2a^{2}\times\cos60^{\circ}=a^{2}$,$2\overrightarrow{FG}\cdot\overrightarrow{SB}=2\times\frac{1}{2}a^{2}\times\cos0^{\circ}=a^{2}$,$4\overrightarrow{FG}\cdot\overrightarrow{EF}=0$,$4\overrightarrow{EF}\cdot\overrightarrow{BA}=4\times\frac{1}{2}a^{2}\times\cos120^{\circ}=-a^{2}$,故选D。
【特别注意】在数量积问题中,求解的关键是正确确定向量的夹角,一定要把两个向量的起点平移到同一位置上。
D【解析】由题意知三棱锥S - ABC为正四面体。如图所示,

取AC的中点D,连接SD,BD,则$SD\perp AC$,$BD\perp AC$,$SD\cap BD = D$,$SD$,$BD\subset$平面SBD,所以$AC\perp$平面SBD。又$SB\subset$平面SBD,所以$AC\perp SB$,点E,F,G分别是SA,SC,BC的中点,所以$FG// SB$,$EF// AC$,所以$EF\perp FG$,且$EF = FG=\frac{1}{2}a$。所以$2\overrightarrow{AS}\cdot\overrightarrow{AB}=2a^{2}\times\cos60^{\circ}=a^{2}$,$2\overrightarrow{FG}\cdot\overrightarrow{SB}=2\times\frac{1}{2}a^{2}\times\cos0^{\circ}=a^{2}$,$4\overrightarrow{FG}\cdot\overrightarrow{EF}=0$,$4\overrightarrow{EF}\cdot\overrightarrow{BA}=4\times\frac{1}{2}a^{2}\times\cos120^{\circ}=-a^{2}$,故选D。
【特别注意】在数量积问题中,求解的关键是正确确定向量的夹角,一定要把两个向量的起点平移到同一位置上。
5. 如图所示,在空间四边形 OABC 中,OB = OC,且∠AOB = ∠AOC = $\frac{\pi}{3}$,则 cos<$\overrightarrow{OA}$,$\overrightarrow{BC}$>的值为( )

A.$\frac{\sqrt{3}}{3}$
B.0
C.$\frac{1}{2}$
D.$\frac{\sqrt{2}}{2}$

A.$\frac{\sqrt{3}}{3}$
B.0
C.$\frac{1}{2}$
D.$\frac{\sqrt{2}}{2}$
答案:
B【解析】$\because$在空间四边形OABC中,$OB = OC$,$\angle AOB = \angle AOC = \frac{\pi}{3}$,$\overrightarrow{BC}=\overrightarrow{OC}-\overrightarrow{OB}$,$\therefore\overrightarrow{OA}\cdot\overrightarrow{BC}=\overrightarrow{OA}\cdot(\overrightarrow{OC}-\overrightarrow{OB})=\overrightarrow{OA}\cdot\overrightarrow{OC}-\overrightarrow{OA}\cdot\overrightarrow{OB}=|\overrightarrow{OA}|\times|\overrightarrow{OC}|\times\cos\frac{\pi}{3}-|\overrightarrow{OA}|\times|\overrightarrow{OB}|\times\cos\frac{\pi}{3}=\frac{1}{2}|\overrightarrow{OA}|\times(|\overrightarrow{OC}|-|\overrightarrow{OB}|)=0$,$\therefore\cos\langle\overrightarrow{OA},\overrightarrow{BC}\rangle=\frac{\overrightarrow{OA}\cdot\overrightarrow{BC}}{|\overrightarrow{OA}|\times|\overrightarrow{BC}|}=0$。故选B。
6. [北京丰台 2024 高二月考]已知空间向量 a,b,c 满足|a| = 2,|b| = 3,|c| = $\sqrt{7}$且 a + b + c = 0,则 a 与 b 的夹角大小为 ( )
A.30°
B.60°
C.120°
D.150°
A.30°
B.60°
C.120°
D.150°
答案:
C【解析】由题意知$c = -(a + b)$,则$c^{2}=(a + b)^{2}=a^{2}+2a\cdot b + b^{2}=4 + 2\times2\times3\times\cos\langle a,b\rangle + 9 = 7$,所以$\cos\langle a,b\rangle=-\frac{1}{2}$。又$\langle a,b\rangle\in[0,\pi]$,可得$\langle a,b\rangle=\frac{2\pi}{3}$,即$\langle a,b\rangle = 120^{\circ}$。故选C。
7. 已知 e₁,e₂为相互垂直的单位向量,且 m = 2e₁ + 3e₂,n = ke₁ - 4e₂,m⊥n,则实数 k 的值为 ( )
A.-6
B.6
C.3
D.-3
A.-6
B.6
C.3
D.-3
答案:
B【解析】由题意知$e_1\cdot e_2 = 0$。由$m\perp n$得$m\cdot n = 0$,即$(2e_1 + 3e_2)\cdot(ke_1 - 4e_2)=0$,$\therefore2k - 12 = 0$,$\therefore k = 6$。故选B。
8. [山东师范大学附属中学 2024 高二月考]如图,在平行六面体 ABCD - A₁B₁C₁D₁ 中,AB = AD,∠BAD = ∠BAA₁ = ∠DAA₁ = 60°.若 A₁C⊥BC₁,则$\frac{AA₁}{AB}$的值为 ( )

A.1
B.$\frac{1}{2}$
C.$\frac{2}{3}$
D.$\frac{3}{2}$

A.1
B.$\frac{1}{2}$
C.$\frac{2}{3}$
D.$\frac{3}{2}$
答案:
D【解析】设$\overrightarrow{AB}=a$,$\overrightarrow{AD}=b$,$\overrightarrow{AA_1}=c$,且$|a| = |b| = m$,$|c| = n$,由向量的线性运算,可得$\overrightarrow{A_1C}=a + b - c$,$\overrightarrow{BC_1}=b + c$。又因为$\overrightarrow{A_1C}\perp\overrightarrow{BC_1}$,$\angle BAD = \angle BAA_1 = \angle DAA_1 = 60^{\circ}$,可得$\overrightarrow{A_1C}\cdot\overrightarrow{BC_1}=(a + b - c)\cdot(b + c)=a\cdot b + a\cdot c + b^{2}-c^{2}=\frac{3}{2}m^{2}+mn - n^{2}=0$,即$2n^{2}-mn - 3m^{2}=0$,即$2(\frac{n}{m})^{2}-\frac{n}{m}-3 = 0$,解得$\frac{n}{m}=\frac{3}{2}$或$\frac{n}{m}=-1$(舍去),即$\frac{|\overrightarrow{AA_1}|}{|\overrightarrow{AB}|}$的值为$\frac{3}{2}$。故选D。
9. [山东新泰一中 2023 高二期中]在棱长为 1 的正方体 ABCD - A₁B₁C₁D₁ 中,向量$\overrightarrow{AB}$在向量$\overrightarrow{A₁C₁}$上的投影向量的模是________.


答案:
$\frac{\sqrt{2}}{2}$【解析】在棱长为1的正方体$ABCD - A_1B_1C_1D_1$中,向量$\overrightarrow{AB}$与向量$\overrightarrow{A_1C_1}$的夹角为$45^{\circ}$,所以$\frac{\overrightarrow{AB}\cdot\overrightarrow{A_1C_1}}{|\overrightarrow{A_1C_1}|}=|\overrightarrow{AB}|\cos\langle\overrightarrow{A_1C_1},\overrightarrow{AB}\rangle=1\times\cos45^{\circ}=\frac{\sqrt{2}}{2}$,即向量$\overrightarrow{AB}$在向量$\overrightarrow{A_1C_1}$上的投影向量的模为$\frac{\sqrt{2}}{2}$。
10. 教材变式[四川南充高中 2024 高二期中]如图,在平行六面体 ABCD - A₁B₁C₁D₁ 中,以顶点 A 为端点的三条棱长度都为 1,且两两夹角为 60°.记$\overrightarrow{AB}$ = a,$\overrightarrow{AD}$ = b,$\overrightarrow{AA₁}$ = c.
(1)求$\overrightarrow{BD₁}$的模;
(2)求$\overrightarrow{BD₁}$与$\overrightarrow{AC}$夹角的余弦值.

(1)求$\overrightarrow{BD₁}$的模;
(2)求$\overrightarrow{BD₁}$与$\overrightarrow{AC}$夹角的余弦值.

答案:
[解]
(1)由题意知$|a| = |b| = |c| = 1$,$\langle a,b\rangle = \langle b,c\rangle = \langle c,a\rangle = 60^{\circ}$,$\therefore a\cdot b = b\cdot c = c\cdot a = 1\times1\times\cos60^{\circ}=\frac{1}{2}$。又$\because\overrightarrow{BD_1}=\overrightarrow{BA}+\overrightarrow{AA_1}+\overrightarrow{A_1D_1}= - a + c + b$,$\therefore\overrightarrow{BD_1}^{2}=(b + c - a)^{2}=b^{2}+c^{2}+a^{2}+2b\cdot c - 2b\cdot a - 2c\cdot a = 1 + 1 + 1 - 1 = 2$,$\therefore|\overrightarrow{BD_1}|=\sqrt{2}$,即$\overrightarrow{BD_1}$的模为$\sqrt{2}$。
(2)$\because\overrightarrow{AC}=\overrightarrow{AB}+\overrightarrow{AD}=a + b$,$\therefore\overrightarrow{AC}^{2}=(a + b)^{2}=a^{2}+2a\cdot b + b^{2}=1 + 2\times\frac{1}{2}+1 = 3$,$\therefore|\overrightarrow{AC}|=\sqrt{3}$。$\therefore\overrightarrow{BD_1}\cdot\overrightarrow{AC}=(b + c - a)\cdot(a + b)=a\cdot b + a\cdot c - a^{2}+b^{2}+b\cdot c - a\cdot b = 1$,$\therefore\cos\langle\overrightarrow{BD_1},\overrightarrow{AC}\rangle=\frac{\overrightarrow{BD_1}\cdot\overrightarrow{AC}}{|\overrightarrow{BD_1}|\times|\overrightarrow{AC}|}=\frac{1}{\sqrt{3}}=\frac{\sqrt{6}}{6}$,即$\overrightarrow{BD_1}$与$\overrightarrow{AC}$夹角的余弦值为$\frac{\sqrt{6}}{6}$。
【链接教材】本题是教材P28第3题的变式与延伸,空间中的线段长度问题,可以用已知模和夹角的向量来表示,再根据求向量的模的公式和数量积运算规律求模。
(1)由题意知$|a| = |b| = |c| = 1$,$\langle a,b\rangle = \langle b,c\rangle = \langle c,a\rangle = 60^{\circ}$,$\therefore a\cdot b = b\cdot c = c\cdot a = 1\times1\times\cos60^{\circ}=\frac{1}{2}$。又$\because\overrightarrow{BD_1}=\overrightarrow{BA}+\overrightarrow{AA_1}+\overrightarrow{A_1D_1}= - a + c + b$,$\therefore\overrightarrow{BD_1}^{2}=(b + c - a)^{2}=b^{2}+c^{2}+a^{2}+2b\cdot c - 2b\cdot a - 2c\cdot a = 1 + 1 + 1 - 1 = 2$,$\therefore|\overrightarrow{BD_1}|=\sqrt{2}$,即$\overrightarrow{BD_1}$的模为$\sqrt{2}$。
(2)$\because\overrightarrow{AC}=\overrightarrow{AB}+\overrightarrow{AD}=a + b$,$\therefore\overrightarrow{AC}^{2}=(a + b)^{2}=a^{2}+2a\cdot b + b^{2}=1 + 2\times\frac{1}{2}+1 = 3$,$\therefore|\overrightarrow{AC}|=\sqrt{3}$。$\therefore\overrightarrow{BD_1}\cdot\overrightarrow{AC}=(b + c - a)\cdot(a + b)=a\cdot b + a\cdot c - a^{2}+b^{2}+b\cdot c - a\cdot b = 1$,$\therefore\cos\langle\overrightarrow{BD_1},\overrightarrow{AC}\rangle=\frac{\overrightarrow{BD_1}\cdot\overrightarrow{AC}}{|\overrightarrow{BD_1}|\times|\overrightarrow{AC}|}=\frac{1}{\sqrt{3}}=\frac{\sqrt{6}}{6}$,即$\overrightarrow{BD_1}$与$\overrightarrow{AC}$夹角的余弦值为$\frac{\sqrt{6}}{6}$。
【链接教材】本题是教材P28第3题的变式与延伸,空间中的线段长度问题,可以用已知模和夹角的向量来表示,再根据求向量的模的公式和数量积运算规律求模。
1. 在正方体 ABCD - A₁B₁C₁D₁ 中,有下列说法:
①($\overrightarrow{AA₁}$ + $\overrightarrow{AD}$ + $\overrightarrow{AB}$)² = 3|$\overrightarrow{AB}$|²;②$\overrightarrow{A₁C}$·($\overrightarrow{A₁B₁}$ - $\overrightarrow{A₁A}$) = 0;③$\overrightarrow{AD₁}$与$\overrightarrow{A₁B}$的夹角为 60°.
其中说法正确的有 ( )
A.1 个
B.2 个
C.3 个
D.0 个
①($\overrightarrow{AA₁}$ + $\overrightarrow{AD}$ + $\overrightarrow{AB}$)² = 3|$\overrightarrow{AB}$|²;②$\overrightarrow{A₁C}$·($\overrightarrow{A₁B₁}$ - $\overrightarrow{A₁A}$) = 0;③$\overrightarrow{AD₁}$与$\overrightarrow{A₁B}$的夹角为 60°.
其中说法正确的有 ( )
A.1 个
B.2 个
C.3 个
D.0 个
答案:
B【解析】由题意知$\overrightarrow{AA_1}+\overrightarrow{AD}+\overrightarrow{AB}=\overrightarrow{AC_1}$,$|\overrightarrow{AC_1}|=\sqrt{3}|\overrightarrow{AB}|$,则$|\overrightarrow{AC_1}|^{2}=3|\overrightarrow{AB}|^{2}$,又知$\overrightarrow{A_1B_1}-\overrightarrow{A_1A}=\overrightarrow{AB}$,$\overrightarrow{A_1C}\perp\overrightarrow{AB}$,则$\overrightarrow{A_1C}\cdot\overrightarrow{AB}=0$,故①②正确。因为$\overrightarrow{AD_1}$与$\overrightarrow{A_1B}$的夹角即为$\overrightarrow{AD_1}$与$\overrightarrow{D_1C}$的夹角,即为$120^{\circ}$,故③不正确。
2. 已知空间向量 a,b,|a| = 1,|b| = $\sqrt{2}$,且 a - b 与 a 垂直,则 a 与 b 的夹角为 ( )
A.60°
B.30°
C.135°
D.45°
A.60°
B.30°
C.135°
D.45°
答案:
D【解析】$\because\vec{a}-\vec{b}$与$\vec{a}$垂直,$\therefore(\vec{a}-\vec{b})\cdot\vec{a}=0$,$\therefore\vec{a}\cdot\vec{a}-\vec{a}\cdot\vec{b}=|\vec{a}|^{2}-|\vec{a}|\cdot|\vec{b}|\cos\langle\vec{a},\vec{b}\rangle=1 - 1\times\sqrt{2}\times\cos\langle\vec{a},\vec{b}\rangle=0$,$\therefore\cos\langle\vec{a},\vec{b}\rangle=\frac{\sqrt{2}}{2}$。$\because0^{\circ}\leq\langle\vec{a},\vec{b}\rangle\leq180^{\circ}$,$\therefore\langle\vec{a},\vec{b}\rangle = 45^{\circ}$。
3. [江苏镇江 2024 高二调研]四棱柱 ABCD - A₁B₁C₁D₁ 的底面 ABCD 是边长为 1 的菱形,侧棱长为 2,且∠C₁CB = ∠C₁CD = ∠BCD = 60°,则线段 A₁C 的长度是 ( )
A.$\sqrt{6}$
B.$\frac{\sqrt{34}}{2}$
C.3
D.$\sqrt{11}$
A.$\sqrt{6}$
B.$\frac{\sqrt{34}}{2}$
C.3
D.$\sqrt{11}$
答案:
D【解析】因为$\angle C_1CB = \angle C_1CD = \angle BCD = 60^{\circ}$,$|\overrightarrow{CD}| = |\overrightarrow{CB}| = 1$,$|\overrightarrow{CC_1}| = 2$,所以$\overrightarrow{CD}\cdot\overrightarrow{CB}=|\overrightarrow{CD}|\times|\overrightarrow{CB}|\times\cos60^{\circ}=\frac{1}{2}$,$\overrightarrow{CD}\cdot\overrightarrow{CC_1}=1$,$\overrightarrow{CB}\cdot\overrightarrow{CC_1}=1$。因为$\overrightarrow{CA_1}=\overrightarrow{CA}+\overrightarrow{AA_1}=\overrightarrow{CA}+\overrightarrow{CC_1}=\overrightarrow{CD}+\overrightarrow{CB}+\overrightarrow{CC_1}$,所以$\overrightarrow{CA_1}^{2}=(\overrightarrow{CD}+\overrightarrow{CB}+\overrightarrow{CC_1})^{2}=|\overrightarrow{CD}|^{2}+|\overrightarrow{CB}|^{2}+|\overrightarrow{CC_1}|^{2}+2\overrightarrow{CD}\cdot\overrightarrow{CB}+2\overrightarrow{CD}\cdot\overrightarrow{CC_1}+2\overrightarrow{CB}\cdot\overrightarrow{CC_1}=1 + 1 + 4 + 2\times\frac{1}{2}+2\times1+2\times1 = 11$,所以$|\overrightarrow{CA_1}|=\sqrt{11}$,即线段$A_1C$的长度是$\sqrt{11}$。故选D。
4. (多选)[辽宁沈阳重点高中联合体 2024 高二期中]已知空间单位向量$\overrightarrow{PA}$,$\overrightarrow{PB}$,$\overrightarrow{PC}$两两之间的夹角均为 60°,$\overrightarrow{PA}$ = 2$\overrightarrow{PE}$,$\overrightarrow{BC}$ = 2$\overrightarrow{BF}$,则下列说法正确的是 ( )
A.$\overrightarrow{PA}$·$\overrightarrow{PB}$ = 1
B.$\overrightarrow{PA}$·($\overrightarrow{BC}$ + $\overrightarrow{AC}$) = -$\frac{1}{2}$
C.|$\overrightarrow{EF}$| = $\frac{\sqrt{2}}{2}$
D.cos<$\overrightarrow{AF}$,$\overrightarrow{CP}$> = $\frac{\sqrt{3}}{6}$
A.$\overrightarrow{PA}$·$\overrightarrow{PB}$ = 1
B.$\overrightarrow{PA}$·($\overrightarrow{BC}$ + $\overrightarrow{AC}$) = -$\frac{1}{2}$
C.|$\overrightarrow{EF}$| = $\frac{\sqrt{2}}{2}$
D.cos<$\overrightarrow{AF}$,$\overrightarrow{CP}$> = $\frac{\sqrt{3}}{6}$
答案:
BC【解析】由空间单位向量$\overrightarrow{PA}$,$\overrightarrow{PB}$,$\overrightarrow{PC}$两两之间的夹角均为$60^{\circ}$,得$\overrightarrow{PA}\cdot\overrightarrow{PB}=1\times1\times\cos60^{\circ}=\frac{1}{2}$,故A错误;$\overrightarrow{PA}\cdot(\overrightarrow{BC}+\overrightarrow{AC})=\overrightarrow{PA}\cdot(\overrightarrow{PC}-\overrightarrow{PB}+\overrightarrow{PC}-\overrightarrow{PA})=\overrightarrow{PA}\cdot(2\overrightarrow{PC}-\overrightarrow{PB}-\overrightarrow{PA})=2\overrightarrow{PA}\cdot\overrightarrow{PC}-\overrightarrow{PA}\cdot\overrightarrow{PB}-\overrightarrow{PA}^{2}=1 - \frac{1}{2}-1 = -\frac{1}{2}$,故B正确;由$\overrightarrow{PA}=2\overrightarrow{PE}$,得$\frac{1}{2}\overrightarrow{PA}=\overrightarrow{PE}$,由$\overrightarrow{BC}=2\overrightarrow{BF}$,得$\overrightarrow{PC}-\overrightarrow{PB}=2\overrightarrow{PF}-2\overrightarrow{PB}$,则$\overrightarrow{PF}=\frac{\overrightarrow{PC}+\overrightarrow{PB}}{2}$,所以$\overrightarrow{EF}=\overrightarrow{PF}-\overrightarrow{PE}=\frac{\overrightarrow{PC}+\overrightarrow{PB}-\overrightarrow{PA}}{2}$,则$|\overrightarrow{EF}|=\frac{|\overrightarrow{PC}+\overrightarrow{PB}-\overrightarrow{PA}|}{2}=\frac{\sqrt{\overrightarrow{PC}^{2}+\overrightarrow{PB}^{2}+\overrightarrow{PA}^{2}+2\overrightarrow{PC}\cdot\overrightarrow{PB}-2\overrightarrow{PC}\cdot\overrightarrow{PA}-2\overrightarrow{PA}\cdot\overrightarrow{PB}}}{2}=\frac{1}{2}\sqrt{1 + 1 + 1 + 1 - 1 - 1}=\frac{\sqrt{2}}{2}$,故C正确;$\overrightarrow{AF}=\overrightarrow{PF}-\overrightarrow{PA}=\frac{\overrightarrow{PC}+\overrightarrow{PB}-2\overrightarrow{PA}}{2}$,所以$\overrightarrow{AF}\cdot\overrightarrow{CP}=-\frac{(\overrightarrow{PC}+\overrightarrow{PB}-2\overrightarrow{PA})\cdot\overrightarrow{PC}}{2}=-\frac{\overrightarrow{PC}^{2}+\overrightarrow{PB}\cdot\overrightarrow{PC}-2\overrightarrow{PA}\cdot\overrightarrow{PC}}{2}=-\frac{1 + \frac{1}{2}-2\times\frac{1}{2}}{2}=-\frac{1}{4}$,故$\cos\langle\overrightarrow{AF},\overrightarrow{CP}\rangle\lt0$,故D错误。故选BC。
5. (多选)[山东日照 2024 高二月考]在自然界中,金刚石是天然存在的最硬的物质.如图①,这是组成金刚石的碳原子在空间中排列的结构示意图,组成金刚石的每个碳原子都与其相邻的 4 个碳原子以完全相同的方式连接.从立体几何的角度来看,可以认为 4 个碳原子分布在一个正四面体的四个顶点处,而中间的那个碳原子处于与这 4 个碳原子距离都相等的位置,如图②所示.这就是说,图②中有 AE = BE = CE = DE,若正四面体 ABCD 的棱长为 4,则 ( )

A.|$\overrightarrow{DE}$| = $\frac{8\sqrt{6}}{9}$
B.$\overrightarrow{EA}$ + $\overrightarrow{EB}$ + $\overrightarrow{EC}$ + $\overrightarrow{ED}$ = 0
C.$\overrightarrow{AE}$·$\overrightarrow{BC}$ = 0
D.$\overrightarrow{AC}$·$\overrightarrow{AE}$ = 8

A.|$\overrightarrow{DE}$| = $\frac{8\sqrt{6}}{9}$
B.$\overrightarrow{EA}$ + $\overrightarrow{EB}$ + $\overrightarrow{EC}$ + $\overrightarrow{ED}$ = 0
C.$\overrightarrow{AE}$·$\overrightarrow{BC}$ = 0
D.$\overrightarrow{AC}$·$\overrightarrow{AE}$ = 8
答案:
BCD【解析】由题意得E是正四面体ABCD外接球的球心。
如图所示,

设点O是顶点A在底面的射影,连接BO,则AO是正四面体ABCD的高,点E在AO上,OB是$\triangle BCD$的外接圆半径。取CD的中点G,AB的中点F,连接AG,BG,GF,则O在BG上,E在FG上,则$OB=\frac{2}{3}BG=\frac{2}{3}\times\frac{\sqrt{3}}{2}\times4=\frac{4\sqrt{3}}{3}$,$AO=\sqrt{AB^{2}-OB^{2}}=\frac{4\sqrt{6}}{3}$。因为$BE^{2}=(AO - AE)^{2}+BO^{2}$,即$AE^{2}=(AO - AE)^{2}+BO^{2}$,则$AE^{2}=(\frac{4\sqrt{6}}{3}-AE)^{2}+(\frac{4\sqrt{3}}{3})^{2}$,解得$AE = \sqrt{6}$。对于A,$|\overrightarrow{DE}| = |\overrightarrow{AE}| = \sqrt{6}$,故A错误;对于B,因为$AG = BG=\frac{\sqrt{3}}{2}\times4 = 2\sqrt{3}$,$FG\perp AB$,$EG\perp CD$,所以$EF=\sqrt{AE^{2}-AF^{2}}=\sqrt{6 - 4}=\sqrt{2}$,$EG=\sqrt{DE^{2}-DG^{2}}=\sqrt{6 - 4}=\sqrt{2}$,则$EF = EG$,又$\overrightarrow{EA}+\overrightarrow{EB}=2\overrightarrow{EF}$,$\overrightarrow{EC}+\overrightarrow{ED}=2\overrightarrow{EG}$,则$\overrightarrow{EA}+\overrightarrow{EB}=-(\overrightarrow{EC}+\overrightarrow{ED})$,所以$\overrightarrow{EA}+\overrightarrow{EB}+\overrightarrow{EC}+\overrightarrow{ED}=0$,故B正确;对于C,因为$AE\perp$底面BCD,$BC\subset$底面BCD,所以$AE\perp BC$,所以$\overrightarrow{AE}\cdot\overrightarrow{BC}=0$,故C正确;对于D,因为$\cos\langle\overrightarrow{AC},\overrightarrow{AE}\rangle=\cos\langle\overrightarrow{AC},\overrightarrow{AO}\rangle=\frac{AO}{AC}=\frac{\frac{4\sqrt{6}}{3}}{4}=\frac{\sqrt{6}}{3}$,所以$\overrightarrow{AC}\cdot\overrightarrow{AE}=|\overrightarrow{AC}|\cdot|\overrightarrow{AE}|\cos\langle\overrightarrow{AC},\overrightarrow{AE}\rangle=4\times\sqrt{6}\times\frac{\sqrt{6}}{3}=8$,故D正确。故选BCD。
BCD【解析】由题意得E是正四面体ABCD外接球的球心。
如图所示,

设点O是顶点A在底面的射影,连接BO,则AO是正四面体ABCD的高,点E在AO上,OB是$\triangle BCD$的外接圆半径。取CD的中点G,AB的中点F,连接AG,BG,GF,则O在BG上,E在FG上,则$OB=\frac{2}{3}BG=\frac{2}{3}\times\frac{\sqrt{3}}{2}\times4=\frac{4\sqrt{3}}{3}$,$AO=\sqrt{AB^{2}-OB^{2}}=\frac{4\sqrt{6}}{3}$。因为$BE^{2}=(AO - AE)^{2}+BO^{2}$,即$AE^{2}=(AO - AE)^{2}+BO^{2}$,则$AE^{2}=(\frac{4\sqrt{6}}{3}-AE)^{2}+(\frac{4\sqrt{3}}{3})^{2}$,解得$AE = \sqrt{6}$。对于A,$|\overrightarrow{DE}| = |\overrightarrow{AE}| = \sqrt{6}$,故A错误;对于B,因为$AG = BG=\frac{\sqrt{3}}{2}\times4 = 2\sqrt{3}$,$FG\perp AB$,$EG\perp CD$,所以$EF=\sqrt{AE^{2}-AF^{2}}=\sqrt{6 - 4}=\sqrt{2}$,$EG=\sqrt{DE^{2}-DG^{2}}=\sqrt{6 - 4}=\sqrt{2}$,则$EF = EG$,又$\overrightarrow{EA}+\overrightarrow{EB}=2\overrightarrow{EF}$,$\overrightarrow{EC}+\overrightarrow{ED}=2\overrightarrow{EG}$,则$\overrightarrow{EA}+\overrightarrow{EB}=-(\overrightarrow{EC}+\overrightarrow{ED})$,所以$\overrightarrow{EA}+\overrightarrow{EB}+\overrightarrow{EC}+\overrightarrow{ED}=0$,故B正确;对于C,因为$AE\perp$底面BCD,$BC\subset$底面BCD,所以$AE\perp BC$,所以$\overrightarrow{AE}\cdot\overrightarrow{BC}=0$,故C正确;对于D,因为$\cos\langle\overrightarrow{AC},\overrightarrow{AE}\rangle=\cos\langle\overrightarrow{AC},\overrightarrow{AO}\rangle=\frac{AO}{AC}=\frac{\frac{4\sqrt{6}}{3}}{4}=\frac{\sqrt{6}}{3}$,所以$\overrightarrow{AC}\cdot\overrightarrow{AE}=|\overrightarrow{AC}|\cdot|\overrightarrow{AE}|\cos\langle\overrightarrow{AC},\overrightarrow{AE}\rangle=4\times\sqrt{6}\times\frac{\sqrt{6}}{3}=8$,故D正确。故选BCD。
6. [辽宁东北育才学校 2024 高二月考]已知空间向量 a,b,c 两两之间的夹角均为 60°,且|a| = 2,|b| = 6,|c| = 2.若向量 x,y 分别满足 y·(y + a - b) = 0 与 x·c = 12,则|y - x|的最小值为________.
答案:
$5 - \sqrt{7}$【解析】依题意得$\vec{a}\cdot\vec{b}=2\times6\times\cos60^{\circ}=6$,$\vec{a}\cdot\vec{c}=2\times2\times\cos60^{\circ}=2$,$\vec{b}\cdot\vec{c}=6\times2\times\cos60^{\circ}=6$。因为$\vec{y}\cdot(\vec{y}+\vec{a}-\vec{b})=0$,所以$\vec{y}^{2}-\vec{y}\cdot(\vec{b}-2\vec{a})=(\vec{y}-\frac{\vec{b}-\vec{a}}{2})^{2}-(\frac{\vec{b}-\vec{a}}{2})^{2}=0$,所以$(\vec{y}-\frac{\vec{b}-\vec{a}}{2})^{2}=\frac{\vec{b}^{2}-2\vec{a}\cdot\vec{b}+\vec{a}^{2}}{4}=7$,所以$|\vec{y}-\frac{\vec{b}-\vec{a}}{2}|=\sqrt{7}$。令$\vec{p}=\frac{\vec{b}-\vec{a}}{2}$,则$|\vec{y}-\vec{p}|=\sqrt{7}$,且$\vec{p}\cdot\vec{c}=\frac{\vec{b}-\vec{a}}{2}\cdot\vec{c}=\frac{\vec{b}\cdot\vec{c}-\vec{a}\cdot\vec{c}}{2}=2$。由$\vec{x}\cdot\vec{c}=12$,得$12 - 2=\vec{x}\cdot\vec{c}-\vec{p}\cdot\vec{c}=(\vec{x}-\vec{p})\cdot\vec{c}\leq|\vec{x}-\vec{p}|\cdot|\vec{c}|$,所以$|\vec{x}-\vec{p}|\geq\frac{10}{2}=5$,所以$|\vec{y}-\vec{x}|=|(\vec{y}-\vec{p})-(\vec{x}-\vec{p})|=|(\vec{x}-\vec{p})-(\vec{y}-\vec{p})|\geq|\vec{x}-\vec{p}|-|\vec{y}-\vec{p}|\geq5 - \sqrt{7}$,当且仅当$\vec{x}-\vec{p}$,$\vec{y}-\vec{p}$,$\vec{c}$共线同向时等号成立。
【名师点拨】解题关键是把已知条件由$\vec{y}\cdot(\vec{y}+\vec{a}-\vec{b})=0$结合已知变形得出$|\vec{y}-\frac{\vec{b}-\vec{a}}{2}|=\sqrt{7}$,引入向量$\vec{p}=\frac{\vec{b}-\vec{a}}{2}$,可得$|\vec{y}-\vec{p}|=\sqrt{7}$,又由$\vec{x}\cdot\vec{c}=12$,得到$|\vec{x}-\vec{p}|$的最小值,从而由向量模的三角不等式得出结论。
【名师点拨】解题关键是把已知条件由$\vec{y}\cdot(\vec{y}+\vec{a}-\vec{b})=0$结合已知变形得出$|\vec{y}-\frac{\vec{b}-\vec{a}}{2}|=\sqrt{7}$,引入向量$\vec{p}=\frac{\vec{b}-\vec{a}}{2}$,可得$|\vec{y}-\vec{p}|=\sqrt{7}$,又由$\vec{x}\cdot\vec{c}=12$,得到$|\vec{x}-\vec{p}|$的最小值,从而由向量模的三角不等式得出结论。
7. [湖北十堰 2024 高二期中]如图,已知正方体 ABCD - A₁B₁C₁D₁ 的棱长为 4,M,N,G 分别是棱 AA₁,BC,A₁D₁ 的中点,设 Q 是该正方体表面上的一点,若$\overrightarrow{MQ}$ = x$\overrightarrow{MG}$ + y$\overrightarrow{MN}$(x,y∈R).
(1)求点 Q 的轨迹围成图形的面积;
(2)求$\overrightarrow{MG}$·$\overrightarrow{MQ}$的最大值.

(1)求点 Q 的轨迹围成图形的面积;
(2)求$\overrightarrow{MG}$·$\overrightarrow{MQ}$的最大值.

答案:
[解]
(1)因为$\overrightarrow{MQ}=x\overrightarrow{MG}+y\overrightarrow{MN}(x,y\in R)$,所以点Q在平面MGN上。如图,
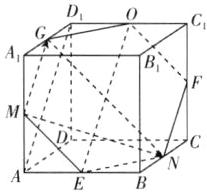
分别取AB,$CC_1$,$C_1D_1$的中点E,F,O,连接OG,OF,FN,EN,ME,$AD_1$,OE,NG。因为M,G分别为$AA_1$,$A_1D_1$的中点,所以$MG// AD_1$。又由正方体$ABCD - A_1B_1C_1D_1$可得$D_0=\frac{1}{2}D_1C_1$,$AE=\frac{1}{2}AB$,$D_1C_1// AB$,$D_1C_1 = AB$,所以$D_0// AE$,且$D_0 = AE$,故四边形$D_0EA$为平行四边形,故$AD_1// OE$,故$MG// OE$,故M,G,O,E四点共面。同理可证N,F,O,E四点共面,同理可证E,N,M,F四点共面,故M,G,O,F,N,E六点共面。由正方体的对称性可得六边形OFNEMG为正六边形,故点Q的轨迹是正六边形OFNEMG。因为正方体$ABCD - A_1B_1C_1D_1$的棱长为4,所以正六边形OFNEMG的边长为$2\sqrt{2}$,所以点Q的轨迹围成图形的面积是$S = 6\times\frac{1}{2}\times2\sqrt{2}\times2\sqrt{2}\times\sin60^{\circ}=12\sqrt{3}$。
(2)如图,
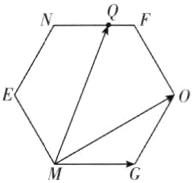
根据向量数量积的几何意义可得,当点Q位于点O时,$\overrightarrow{MG}\cdot\overrightarrow{MQ}$最大;故$\overrightarrow{MG}\cdot\overrightarrow{MQ}=|\overrightarrow{MG}|\times|\overrightarrow{MQ}|\cos\angle QMG=2\sqrt{2}\times|\overrightarrow{MQ}|\cos\angle QMG\leq2\sqrt{2}\times|\overrightarrow{MO}|\cos30^{\circ}=2\sqrt{2}\times2\sqrt{6}\times\cos30^{\circ}=12$,所以$\overrightarrow{MG}\cdot\overrightarrow{MQ}$的最大值为12。
[解]
(1)因为$\overrightarrow{MQ}=x\overrightarrow{MG}+y\overrightarrow{MN}(x,y\in R)$,所以点Q在平面MGN上。如图,

分别取AB,$CC_1$,$C_1D_1$的中点E,F,O,连接OG,OF,FN,EN,ME,$AD_1$,OE,NG。因为M,G分别为$AA_1$,$A_1D_1$的中点,所以$MG// AD_1$。又由正方体$ABCD - A_1B_1C_1D_1$可得$D_0=\frac{1}{2}D_1C_1$,$AE=\frac{1}{2}AB$,$D_1C_1// AB$,$D_1C_1 = AB$,所以$D_0// AE$,且$D_0 = AE$,故四边形$D_0EA$为平行四边形,故$AD_1// OE$,故$MG// OE$,故M,G,O,E四点共面。同理可证N,F,O,E四点共面,同理可证E,N,M,F四点共面,故M,G,O,F,N,E六点共面。由正方体的对称性可得六边形OFNEMG为正六边形,故点Q的轨迹是正六边形OFNEMG。因为正方体$ABCD - A_1B_1C_1D_1$的棱长为4,所以正六边形OFNEMG的边长为$2\sqrt{2}$,所以点Q的轨迹围成图形的面积是$S = 6\times\frac{1}{2}\times2\sqrt{2}\times2\sqrt{2}\times\sin60^{\circ}=12\sqrt{3}$。
(2)如图,

根据向量数量积的几何意义可得,当点Q位于点O时,$\overrightarrow{MG}\cdot\overrightarrow{MQ}$最大;故$\overrightarrow{MG}\cdot\overrightarrow{MQ}=|\overrightarrow{MG}|\times|\overrightarrow{MQ}|\cos\angle QMG=2\sqrt{2}\times|\overrightarrow{MQ}|\cos\angle QMG\leq2\sqrt{2}\times|\overrightarrow{MO}|\cos30^{\circ}=2\sqrt{2}\times2\sqrt{6}\times\cos30^{\circ}=12$,所以$\overrightarrow{MG}\cdot\overrightarrow{MQ}$的最大值为12。
1. [辽宁沈阳市郊联体2024高二期末]在空间直角坐标系中,已知点A(2,3, - 5),B(0, - 2, - 2),C( - 2,t,1),若A,B,C三点共线,则实数t的值为 ( )
A. - 2
B. - 7
C. 10
D. 13
A. - 2
B. - 7
C. 10
D. 13
答案:
B 【解析】因为$\overrightarrow{AB}=(-2,-5,3)$,$\overrightarrow{AC}=(-4,t - 3,6)$,且$A$,$B$,$C$三点共线,所以存在实数$\lambda$,使得$\overrightarrow{AB}=\lambda\overrightarrow{AC}$,则有$\begin{cases}-2=-4\lambda\\-5=\lambda(t - 3)\\3 = 6\lambda\end{cases}$,解得$\begin{cases}\lambda=\frac{1}{2}\\t=-7\end{cases}$,故选 B.
2. 已知空间四点O,A,B,P满足$\overrightarrow{OP}=m\overrightarrow{OA}+n\overrightarrow{OB}$,其中m + n = 1,则下列说法正确的是 ( )
A. 点P一定在直线AB上
B. 点P一定不在直线AB上
C. 点P不一定在直线AB上
D. 以上都不对
A. 点P一定在直线AB上
B. 点P一定不在直线AB上
C. 点P不一定在直线AB上
D. 以上都不对
答案:
A 【解析】由$m + n = 1$得$m = 1 - n$,结合题意知$\overrightarrow{OP}=(1 - n)\overrightarrow{OA}+n\overrightarrow{OB}=\overrightarrow{OA}+n(\overrightarrow{OB}-\overrightarrow{OA})$,即$\overrightarrow{OP}-\overrightarrow{OA}=n(\overrightarrow{OB}-\overrightarrow{OA})$,即$\overrightarrow{AP}=n\overrightarrow{AB}$,据此可知,$A$,$P$,$B$三点共线,点$P$一定在直线$AB$上.
3. 已知非零空间向量$\boldsymbol{e}_{1}$,$\boldsymbol{e}_{2}$不共线,使$k\boldsymbol{e}_{1}+\boldsymbol{e}_{2}$与$\boldsymbol{e}_{1}+k\boldsymbol{e}_{2}$共线的k的值是________.
答案:
$\pm1$ 【解析】若$k\boldsymbol{e}_{1}+\boldsymbol{e}_{2}$与$\boldsymbol{e}_{1}+k\boldsymbol{e}_{2}$共线,则存在实数$\lambda$,使得$k\boldsymbol{e}_{1}+\boldsymbol{e}_{2}=\lambda(\boldsymbol{e}_{1}+k\boldsymbol{e}_{2})$,$\therefore\begin{cases}k=\lambda\\\lambda k = 1\end{cases}$,解得$k=\pm1$.
4. [河南郑州四中2024高二期中]给出下列命题:
①若A,B,C,D是空间任意四点,则有$\overrightarrow{AB}+\overrightarrow{BC}+\overrightarrow{CD}+\overrightarrow{DA}=\boldsymbol{0}$;
②$|\boldsymbol{a}|-|\boldsymbol{b}| = |\boldsymbol{a}+\boldsymbol{b}|$是$\boldsymbol{a}$,$\boldsymbol{b}$共线的充要条件;
③若$\overrightarrow{AB}$,$\overrightarrow{CD}$共线,则AB//CD;
④对空间任意一点O与不共线的三点A,B,C,若$\overrightarrow{OP}=x\overrightarrow{OA}+y\overrightarrow{OB}+z\overrightarrow{OC}$(其中$x,y,z\in\mathbf{R}$),则P,A,B,C四点共面.
其中假命题的个数是 ( )
A. 1
B. 2
C. 3
D. 4
①若A,B,C,D是空间任意四点,则有$\overrightarrow{AB}+\overrightarrow{BC}+\overrightarrow{CD}+\overrightarrow{DA}=\boldsymbol{0}$;
②$|\boldsymbol{a}|-|\boldsymbol{b}| = |\boldsymbol{a}+\boldsymbol{b}|$是$\boldsymbol{a}$,$\boldsymbol{b}$共线的充要条件;
③若$\overrightarrow{AB}$,$\overrightarrow{CD}$共线,则AB//CD;
④对空间任意一点O与不共线的三点A,B,C,若$\overrightarrow{OP}=x\overrightarrow{OA}+y\overrightarrow{OB}+z\overrightarrow{OC}$(其中$x,y,z\in\mathbf{R}$),则P,A,B,C四点共面.
其中假命题的个数是 ( )
A. 1
B. 2
C. 3
D. 4
答案:
C 【解析】①若$A$,$B$,$C$,$D$是空间任意四点,则有$\overrightarrow{AB}+\overrightarrow{BC}+\overrightarrow{CD}+\overrightarrow{DA}=\boldsymbol{0}$,①是真命题.
②$||\boldsymbol{a}|-|\boldsymbol{b}||=|\boldsymbol{a}+\boldsymbol{b}|$或$|\boldsymbol{a}|+|\boldsymbol{b}|=|\boldsymbol{a}+\boldsymbol{b}|$是$\boldsymbol{a}$,$\boldsymbol{b}$共线的充要条件,②是假命题.
③若$\overrightarrow{AB}$,$\overrightarrow{CD}$共线,则$AB// CD$或$AB$与$CD$重合,③是假命题.
④对空间不共线的三点$A$,$B$,$C$与不在平面$ABC$上的任意一点$O$,若$\overrightarrow{OP}=x\overrightarrow{OA}+y\overrightarrow{OB}+z\overrightarrow{OC}$(其中$x$,$y$,$z\in\mathbf{R}$),当且仅当$x + y + z = 1$时,$P$,$A$,$B$,$C$四点共面,④是假命题. 故选 C.
②$||\boldsymbol{a}|-|\boldsymbol{b}||=|\boldsymbol{a}+\boldsymbol{b}|$或$|\boldsymbol{a}|+|\boldsymbol{b}|=|\boldsymbol{a}+\boldsymbol{b}|$是$\boldsymbol{a}$,$\boldsymbol{b}$共线的充要条件,②是假命题.
③若$\overrightarrow{AB}$,$\overrightarrow{CD}$共线,则$AB// CD$或$AB$与$CD$重合,③是假命题.
④对空间不共线的三点$A$,$B$,$C$与不在平面$ABC$上的任意一点$O$,若$\overrightarrow{OP}=x\overrightarrow{OA}+y\overrightarrow{OB}+z\overrightarrow{OC}$(其中$x$,$y$,$z\in\mathbf{R}$),当且仅当$x + y + z = 1$时,$P$,$A$,$B$,$C$四点共面,④是假命题. 故选 C.
5. 已知A,B,C三点不共线,O为平面ABC外一点. 若由$\overrightarrow{OM}=3\overrightarrow{OA}-\overrightarrow{OB}+\lambda\overrightarrow{OC}$确定的点M与A,B,C共面,则$\lambda$的值为 ( )
A. - 2
B. - 1
C. 1
D. 2
A. - 2
B. - 1
C. 1
D. 2
答案:
B 【解析】由点$M$与$A$,$B$,$C$共面,且$\overrightarrow{OM}=3\overrightarrow{OA}-\overrightarrow{OB}+\lambda\overrightarrow{OC}$,可得$3 - 1+\lambda = 1$,解得$\lambda=-1$,故选 B.
6. (多选)[广东肇庆第一中学2023高二期中]在下列条件中,不能使M与A,B,C一定共面的是 ( )
A. $\overrightarrow{OM}=2\overrightarrow{OA}-\overrightarrow{OB}-\overrightarrow{OC}$
B. $\overrightarrow{OM}=\frac{1}{5}\overrightarrow{OA}+\frac{1}{3}\overrightarrow{OB}+\frac{1}{2}\overrightarrow{OC}$
C. $\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}=\boldsymbol{0}$
D. $\overrightarrow{OM}+\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}=\boldsymbol{0}$
A. $\overrightarrow{OM}=2\overrightarrow{OA}-\overrightarrow{OB}-\overrightarrow{OC}$
B. $\overrightarrow{OM}=\frac{1}{5}\overrightarrow{OA}+\frac{1}{3}\overrightarrow{OB}+\frac{1}{2}\overrightarrow{OC}$
C. $\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}=\boldsymbol{0}$
D. $\overrightarrow{OM}+\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}=\boldsymbol{0}$
答案:
ABD 【解析】对于 A 选项,由于$2 - 1 - 1 = 0\neq1$,所以不能得出$M$,$A$,$B$,$C$共面.
对于 B 选项,由于$\frac{1}{5}+\frac{1}{3}+\frac{1}{2}\neq1$,所以不能得出$M$,$A$,$B$,$C$共面.
对于 C 选项,由于$\overrightarrow{MA}=-\overrightarrow{MB}-\overrightarrow{MC}$,则$\overrightarrow{MA}$,$\overrightarrow{MB}$,$\overrightarrow{MC}$为共面向量,所以$M$,$A$,$B$,$C$共面.
对于 D 选项,由$\overrightarrow{OM}+\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}=\boldsymbol{0}$得$\overrightarrow{OM}=-\overrightarrow{OA}-\overrightarrow{OB}-\overrightarrow{OC}$,而$-1 - 1 - 1=-3\neq1$,所以不能得出$M$,$A$,$B$,$C$共面. 故选 ABD.
【归纳总结】证明空间中四点共面的方法
对于空间四点$P$,$M$,$A$,$B$,可以通过证明下列结论成立来证明四点共面:
(1)$\overrightarrow{MP}=x\overrightarrow{MA}+y\overrightarrow{MB}$;
(2)对空间任一点$O$,$\overrightarrow{OP}=\overrightarrow{OM}+x\overrightarrow{MA}+y\overrightarrow{MB}$;
(3)对空间任一点$O$,$\overrightarrow{OP}=x\overrightarrow{OA}+y\overrightarrow{OB}+z\overrightarrow{OM}(x + y + z = 1)$;
(4)$\overrightarrow{PM}//\overrightarrow{AB}$(或$\overrightarrow{PA}//\overrightarrow{MB}$或$\overrightarrow{PB}//\overrightarrow{AM}$).
对于 B 选项,由于$\frac{1}{5}+\frac{1}{3}+\frac{1}{2}\neq1$,所以不能得出$M$,$A$,$B$,$C$共面.
对于 C 选项,由于$\overrightarrow{MA}=-\overrightarrow{MB}-\overrightarrow{MC}$,则$\overrightarrow{MA}$,$\overrightarrow{MB}$,$\overrightarrow{MC}$为共面向量,所以$M$,$A$,$B$,$C$共面.
对于 D 选项,由$\overrightarrow{OM}+\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}=\boldsymbol{0}$得$\overrightarrow{OM}=-\overrightarrow{OA}-\overrightarrow{OB}-\overrightarrow{OC}$,而$-1 - 1 - 1=-3\neq1$,所以不能得出$M$,$A$,$B$,$C$共面. 故选 ABD.
【归纳总结】证明空间中四点共面的方法
对于空间四点$P$,$M$,$A$,$B$,可以通过证明下列结论成立来证明四点共面:
(1)$\overrightarrow{MP}=x\overrightarrow{MA}+y\overrightarrow{MB}$;
(2)对空间任一点$O$,$\overrightarrow{OP}=\overrightarrow{OM}+x\overrightarrow{MA}+y\overrightarrow{MB}$;
(3)对空间任一点$O$,$\overrightarrow{OP}=x\overrightarrow{OA}+y\overrightarrow{OB}+z\overrightarrow{OM}(x + y + z = 1)$;
(4)$\overrightarrow{PM}//\overrightarrow{AB}$(或$\overrightarrow{PA}//\overrightarrow{MB}$或$\overrightarrow{PB}//\overrightarrow{AM}$).
7. [山东省实验中学2024高二期末]已知O为空间任意一点,A,B,C,P满足任意三点不共线但四点共面,且$\overrightarrow{BP}=m\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}$,则实数m的值为 ( )
A. - 1
B. 2
C. - 2
D. - 3
A. - 1
B. 2
C. - 2
D. - 3
答案:
C 【解析】因为$O$为空间任意一点,$\overrightarrow{BP}=m\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}$,所以$\overrightarrow{OP}-\overrightarrow{OB}=m\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}$,所以$\overrightarrow{OP}=m\overrightarrow{OA}+2\overrightarrow{OB}+\overrightarrow{OC}$,因为$A$,$B$,$C$,$P$满足任意三点不共线,但四点共面,所以$m + 2 + 1 = 1$,解得$m=-2$. 故选 C.
8. 如图所示,M,N分别是空间四边形ABCD的边AB,CD的中点. 试判断向量$\overrightarrow{MN}$与向量$\overrightarrow{AD}$,$\overrightarrow{BC}$是否共面.


答案:
【解】由题图可得$\overrightarrow{MN}=\overrightarrow{MA}+\overrightarrow{AD}+\overrightarrow{DN}$,①$\overrightarrow{MN}=\overrightarrow{MB}+\overrightarrow{BC}+\overrightarrow{CN}$,②$\overrightarrow{MA}=-\overrightarrow{MB}$,$\overrightarrow{DN}=-\overrightarrow{CN}$.
因此,①+②得$2\overrightarrow{MN}=\overrightarrow{AD}+\overrightarrow{BC}$,即$\overrightarrow{MN}=\frac{1}{2}\overrightarrow{AD}+\frac{1}{2}\overrightarrow{BC}$,故向量$\overrightarrow{MN}$与向量$\overrightarrow{AD}$,$\overrightarrow{BC}$共面.
因此,①+②得$2\overrightarrow{MN}=\overrightarrow{AD}+\overrightarrow{BC}$,即$\overrightarrow{MN}=\frac{1}{2}\overrightarrow{AD}+\frac{1}{2}\overrightarrow{BC}$,故向量$\overrightarrow{MN}$与向量$\overrightarrow{AD}$,$\overrightarrow{BC}$共面.
9. [内蒙古赤峰2024高二期中]在长方体ABCD - $A_{1}B_{1}C_{1}D_{1}$中,可以作为空间的一个基底的是 ( )
A. $\overrightarrow{AB}$,$\overrightarrow{AC}$,$\overrightarrow{AD}$
B. $\overrightarrow{AB}$,$\overrightarrow{AA_{1}}$,$\overrightarrow{AB_{1}}$
C. $\overrightarrow{D_{1}A_{1}}$,$\overrightarrow{D_{1}C_{1}}$,$\overrightarrow{D_{1}D}$
D. $\overrightarrow{AC_{1}}$,$\overrightarrow{A_{1}C}$,$\overrightarrow{BB_{1}}$
A. $\overrightarrow{AB}$,$\overrightarrow{AC}$,$\overrightarrow{AD}$
B. $\overrightarrow{AB}$,$\overrightarrow{AA_{1}}$,$\overrightarrow{AB_{1}}$
C. $\overrightarrow{D_{1}A_{1}}$,$\overrightarrow{D_{1}C_{1}}$,$\overrightarrow{D_{1}D}$
D. $\overrightarrow{AC_{1}}$,$\overrightarrow{A_{1}C}$,$\overrightarrow{BB_{1}}$
答案:
C 【解析】长方体$ABCD - A_{1}B_{1}C_{1}D_{1}$如图所示.

对于 A,因为$\overrightarrow{AC}=\overrightarrow{AB}+\overrightarrow{AD}$,所以$\overrightarrow{AB}$,$\overrightarrow{AC}$,$\overrightarrow{AD}$共面,故$\overrightarrow{AB}$,$\overrightarrow{AC}$,$\overrightarrow{AD}$不能作为基底,故 A 错误;
对于 B,因为$\overrightarrow{AB_{1}}=\overrightarrow{AB}+\overrightarrow{AA_{1}}$,所以$\overrightarrow{AB}$,$\overrightarrow{AA_{1}}$,$\overrightarrow{AB_{1}}$共面,故$\overrightarrow{AB}$,$\overrightarrow{AA_{1}}$,$\overrightarrow{AB_{1}}$不能作为基底,故 B 错误;
对于 C,因为$\overrightarrow{D_{1}A_{1}}$,$\overrightarrow{D_{1}C_{1}}$,$\overrightarrow{D_{1}D}$不共面,所以$\overrightarrow{D_{1}A_{1}}$,$\overrightarrow{D_{1}C_{1}}$,$\overrightarrow{D_{1}D}$可以作为基底,故 C 正确;
对于 D,因为$\overrightarrow{AC_{1}}$,$\overrightarrow{A_{1}C}$,$\overrightarrow{CC_{1}}$共面,且$\overrightarrow{BB_{1}}=\overrightarrow{CC_{1}}$,所以$\overrightarrow{AC_{1}}$,$\overrightarrow{A_{1}C}$,$\overrightarrow{BB_{1}}$共面,故$\overrightarrow{AC_{1}}$,$\overrightarrow{A_{1}C}$,$\overrightarrow{BB_{1}}$不能作为基底,故 D 错误. 故选 C.
【归纳总结】基底的判断
判断三个向量能否构成空间的一组基底,关键是判断它们是否共面,若从正面判断难以入手,可以用反证法进行判断. 假设向量$\boldsymbol{a}+\boldsymbol{b}$,$\boldsymbol{b}+\boldsymbol{c}$,$\boldsymbol{c}+\boldsymbol{a}$不能构成空间的一个基底,看是否存在一对实数$\lambda$,$\mu$,使得$\boldsymbol{a}+\boldsymbol{b}=\lambda(\boldsymbol{b}+\boldsymbol{c})+\mu(\boldsymbol{c}+\boldsymbol{a})$,若存在,则假设成立;若不存在,则假设不成立.
C 【解析】长方体$ABCD - A_{1}B_{1}C_{1}D_{1}$如图所示.

对于 A,因为$\overrightarrow{AC}=\overrightarrow{AB}+\overrightarrow{AD}$,所以$\overrightarrow{AB}$,$\overrightarrow{AC}$,$\overrightarrow{AD}$共面,故$\overrightarrow{AB}$,$\overrightarrow{AC}$,$\overrightarrow{AD}$不能作为基底,故 A 错误;
对于 B,因为$\overrightarrow{AB_{1}}=\overrightarrow{AB}+\overrightarrow{AA_{1}}$,所以$\overrightarrow{AB}$,$\overrightarrow{AA_{1}}$,$\overrightarrow{AB_{1}}$共面,故$\overrightarrow{AB}$,$\overrightarrow{AA_{1}}$,$\overrightarrow{AB_{1}}$不能作为基底,故 B 错误;
对于 C,因为$\overrightarrow{D_{1}A_{1}}$,$\overrightarrow{D_{1}C_{1}}$,$\overrightarrow{D_{1}D}$不共面,所以$\overrightarrow{D_{1}A_{1}}$,$\overrightarrow{D_{1}C_{1}}$,$\overrightarrow{D_{1}D}$可以作为基底,故 C 正确;
对于 D,因为$\overrightarrow{AC_{1}}$,$\overrightarrow{A_{1}C}$,$\overrightarrow{CC_{1}}$共面,且$\overrightarrow{BB_{1}}=\overrightarrow{CC_{1}}$,所以$\overrightarrow{AC_{1}}$,$\overrightarrow{A_{1}C}$,$\overrightarrow{BB_{1}}$共面,故$\overrightarrow{AC_{1}}$,$\overrightarrow{A_{1}C}$,$\overrightarrow{BB_{1}}$不能作为基底,故 D 错误. 故选 C.
【归纳总结】基底的判断
判断三个向量能否构成空间的一组基底,关键是判断它们是否共面,若从正面判断难以入手,可以用反证法进行判断. 假设向量$\boldsymbol{a}+\boldsymbol{b}$,$\boldsymbol{b}+\boldsymbol{c}$,$\boldsymbol{c}+\boldsymbol{a}$不能构成空间的一个基底,看是否存在一对实数$\lambda$,$\mu$,使得$\boldsymbol{a}+\boldsymbol{b}=\lambda(\boldsymbol{b}+\boldsymbol{c})+\mu(\boldsymbol{c}+\boldsymbol{a})$,若存在,则假设成立;若不存在,则假设不成立.
10. (多选)[四川绵阳南山中学2024高二月考]已知$\{\boldsymbol{a},\boldsymbol{b},\boldsymbol{c}\}$是空间的一组基底,则下列说法正确的是 ( )
A. $\boldsymbol{a}\cdot(\boldsymbol{b}\cdot\boldsymbol{c}) = (\boldsymbol{a}\cdot\boldsymbol{b})\cdot\boldsymbol{c}$
B. 若$x\boldsymbol{a}+y\boldsymbol{b}+z\boldsymbol{c}=\boldsymbol{0}$,则$x = y = z = 0$
C. $\boldsymbol{a}$在$\boldsymbol{b}$上的投影向量为$\frac{(\boldsymbol{a}\cdot\boldsymbol{b})\boldsymbol{b}}{\boldsymbol{b}^{2}}$
D. $\boldsymbol{a}+\boldsymbol{b}$,$\boldsymbol{b}-\boldsymbol{c}$,$\boldsymbol{c}+2\boldsymbol{a}$一定能构成空间的一组基底
A. $\boldsymbol{a}\cdot(\boldsymbol{b}\cdot\boldsymbol{c}) = (\boldsymbol{a}\cdot\boldsymbol{b})\cdot\boldsymbol{c}$
B. 若$x\boldsymbol{a}+y\boldsymbol{b}+z\boldsymbol{c}=\boldsymbol{0}$,则$x = y = z = 0$
C. $\boldsymbol{a}$在$\boldsymbol{b}$上的投影向量为$\frac{(\boldsymbol{a}\cdot\boldsymbol{b})\boldsymbol{b}}{\boldsymbol{b}^{2}}$
D. $\boldsymbol{a}+\boldsymbol{b}$,$\boldsymbol{b}-\boldsymbol{c}$,$\boldsymbol{c}+2\boldsymbol{a}$一定能构成空间的一组基底
答案:
BCD 【解析】A 选项,当$\boldsymbol{a}$,$\boldsymbol{c}$不共线时,$\boldsymbol{a}\cdot(\boldsymbol{b}\cdot\boldsymbol{c})$与$\boldsymbol{a}$共线,$(\boldsymbol{a}\cdot\boldsymbol{b})\cdot\boldsymbol{c}$与$\boldsymbol{c}$共线,故$\boldsymbol{a}\cdot(\boldsymbol{b}\cdot\boldsymbol{c})=(\boldsymbol{a}\cdot\boldsymbol{b})\cdot\boldsymbol{c}$不可能成立,故 A 不正确. B 选项,$\{\boldsymbol{a},\boldsymbol{b},\boldsymbol{c}\}$是空间的一组基底,故三个向量不共面且两两共面不共线,假设$x$,$y$,$z$不全为$0$,不妨设$x\neq0$,此时有$x\boldsymbol{a}=\boldsymbol{0}$,故$\boldsymbol{a}=\boldsymbol{0}$,矛盾;不妨设$x\neq0$,$y\neq0$,此时$x\boldsymbol{a}+y\boldsymbol{b}=\boldsymbol{0}$,故$\boldsymbol{a}$,$\boldsymbol{b}$共线,矛盾;若三者均不为$0$,即$x\boldsymbol{a}+y\boldsymbol{b}+z\boldsymbol{c}=\boldsymbol{0}$,此时$\boldsymbol{a}$,$\boldsymbol{b}$,$\boldsymbol{c}$共面,矛盾,综上,假设不成立,故$x = y = z = 0$,B 正确. C 选项,$\boldsymbol{a}$在$\boldsymbol{b}$上的投影向量为$\frac{(\boldsymbol{a}\cdot\boldsymbol{b})\boldsymbol{b}}{b^{2}}$,C 正确. D 选项,设$\boldsymbol{a}+\boldsymbol{b}=m(\boldsymbol{b}-\boldsymbol{c})+n(\boldsymbol{c}+2\boldsymbol{a})$,即$\begin{cases}2n = 1\\m = 1\\-m + n = 0\end{cases}$无解,故$\boldsymbol{a}+\boldsymbol{b}$,$\boldsymbol{b}-\boldsymbol{c}$,$\boldsymbol{c}+2\boldsymbol{a}$不共面,一定能构成空间的一组基底,D 正确. 故选 BCD.
查看更多完整答案,请扫码查看


