《2024年高中必刷题高二数学选择性必修第一册人教B版》

9. [河南南阳一中2024高二月考]如图，在三棱柱ABC - A₁B₁C₁中，E，F分别是BC，CC₁的中点，G为△ABC的重心，则$\overrightarrow{GF}=$（ ）


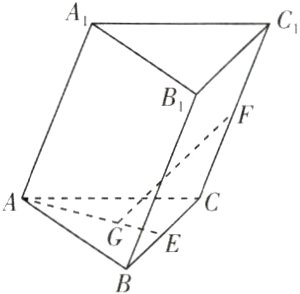
A. $-\frac{1}{3}\overrightarrow{AB}+\frac{2}{3}\overrightarrow{AC}+\frac{1}{2}\overrightarrow{AA_{1}}$
B. $\frac{1}{3}\overrightarrow{AB}+\frac{2}{3}\overrightarrow{AC}+\frac{1}{2}\overrightarrow{AA_{1}}$
C. $-\frac{2}{3}\overrightarrow{AB}+\frac{1}{3}\overrightarrow{AC}-\frac{1}{2}\overrightarrow{AA_{1}}$
D. $\frac{1}{3}\overrightarrow{AB}-\frac{2}{3}\overrightarrow{AC}+\frac{1}{2}\overrightarrow{AA_{1}}$

答案： A 【解析】由题意可得$\overrightarrow{GF}=\overrightarrow{GE}+\overrightarrow{EF}=\frac{1}{3}\overrightarrow{AE}+\frac{1}{2}\overrightarrow{BC_{1}}=\frac{1}{3}\times\frac{1}{2}(\overrightarrow{AB}+\overrightarrow{AC})+\frac{1}{2}(\overrightarrow{BC}+\overrightarrow{BB_{1}})=\frac{1}{6}\overrightarrow{AB}+\frac{1}{6}\overrightarrow{AC}+\frac{1}{2}(\overrightarrow{AC}-\overrightarrow{AB}+\overrightarrow{BB_{1}})=-\frac{1}{3}\overrightarrow{AB}+\frac{2}{3}\overrightarrow{AC}+\frac{1}{2}\overrightarrow{BB_{1}}=-\frac{1}{3}\overrightarrow{AB}+\frac{2}{3}\overrightarrow{AC}+\frac{1}{2}\overrightarrow{AA_{1}}$. 故选A.
【规律方法】三角形$ABC$的重心$G$为三角形三条中线的交点，同时也是中线的三等分点.

10. [山东菏泽一中2024高二月考]在四面体OABC中，E为OA中点，$\overrightarrow{CF}=\frac{1}{3}\overrightarrow{CB}$，若$\overrightarrow{OA}=\boldsymbol{a},\overrightarrow{OB}=\boldsymbol{b},\overrightarrow{OC}=\boldsymbol{c}$，则$\overrightarrow{EF}=$（ ）
A. $\frac{1}{2}\boldsymbol{a}-\frac{1}{3}\boldsymbol{b}-\frac{2}{3}\boldsymbol{c}$
B. $-\frac{1}{2}\boldsymbol{a}-\frac{1}{3}\boldsymbol{b}+\frac{4}{3}\boldsymbol{c}$
C. $-\frac{1}{2}\boldsymbol{a}+\frac{2}{3}\boldsymbol{b}+\frac{1}{3}\boldsymbol{c}$
D. $-\frac{1}{2}\boldsymbol{a}+\frac{1}{3}\boldsymbol{b}+\frac{2}{3}\boldsymbol{c}$

答案： D 【解析】$\overrightarrow{EF}=\overrightarrow{EO}+\overrightarrow{OF}=-\frac{1}{2}\overrightarrow{OA}+\overrightarrow{OC}+\overrightarrow{CF}=-\frac{1}{2}\overrightarrow{OA}+\overrightarrow{OC}+\frac{1}{3}\overrightarrow{CB}=-\frac{1}{2}\overrightarrow{OA}+\overrightarrow{OC}+\frac{1}{3}(\overrightarrow{OB}-\overrightarrow{OC})=-\frac{1}{2}\boldsymbol{a}+\frac{1}{3}\boldsymbol{b}+\frac{2}{3}\boldsymbol{c}$. 故选D.

11. [内蒙古呼和浩特2024高二期中]如图，棱长为1的正四面体（四个面都是正三角形）OABC，M是棱BC的中点，点N在线段OM上，且$MN = \frac{1}{2}ON$. 用向量$\overrightarrow{OA},\overrightarrow{OB},\overrightarrow{OC}$表示$\overrightarrow{AN}$.

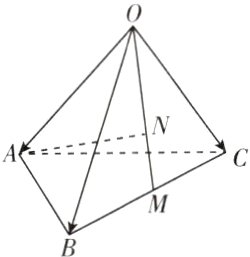
答案： 【解】$\overrightarrow{AN}=\overrightarrow{AO}+\overrightarrow{ON}=\overrightarrow{AO}+\frac{2}{3}\overrightarrow{OM}=\overrightarrow{AO}+\frac{2}{3}\times\frac{1}{2}(\overrightarrow{OB}+\overrightarrow{OC})=-\overrightarrow{OA}+\frac{1}{3}\overrightarrow{OB}+\frac{1}{3}\overrightarrow{OC}$，所以$\overrightarrow{AN}=-\overrightarrow{OA}+\frac{1}{3}\overrightarrow{OB}+\frac{1}{3}\overrightarrow{OC}$.
【归纳总结】对空间向量进行线性运算时，要尽可能地使空间向量转化为平行四边形或三角形中的向量，运用向量加法的平行四边形法则、三角形法则，以及利用三角形的中位线、相似三角形、线段的比例等平面几何的性质，把未知向量转化为与已知向量有直接关系的向量进行运算.

12. [福建莆田2024高二月考]已知不共线向量$\boldsymbol{e}_{1},\boldsymbol{e}_{2},\boldsymbol{e}_{3}$，$\overrightarrow{OP}=\boldsymbol{e}_{1}-2\boldsymbol{e}_{2}+\boldsymbol{e}_{3}$，$\overrightarrow{PQ}=-5\boldsymbol{e}_{1}-6\boldsymbol{e}_{2}+4\boldsymbol{e}_{3}$，$\overrightarrow{QR}=7\boldsymbol{e}_{1}+2\boldsymbol{e}_{2}-2\boldsymbol{e}_{3}$，则一定共线的三个点是（ ）
A. O，P，Q B. P，Q，R
C. O，Q，R D. O，P，R

答案： D 【解析】若$\overrightarrow{OP}//\overrightarrow{PQ}$，则存在唯一实数$\lambda _{1}$使得$\overrightarrow{OP}=\lambda _{1}\overrightarrow{PQ}$，即$\boldsymbol{e}_{1}-2\boldsymbol{e}_{2}+\boldsymbol{e}_{3}=\lambda _{1}(-5\boldsymbol{e}_{1}-6\boldsymbol{e}_{2}+4\boldsymbol{e}_{3})$，所以$\begin{cases}1 = - 5\lambda _{1},\\-2 = - 6\lambda _{1},\\1 = 4\lambda _{1}\end{cases}$，无解，所以$\overrightarrow{OP}$，$\overrightarrow{PQ}$不共线，则$O$，$P$，$Q$三点不共线；若$\overrightarrow{QR}//\overrightarrow{PQ}$，则存在唯一实数$\lambda _{2}$使得$\overrightarrow{QR}=\lambda _{2}\overrightarrow{PQ}$，即$7\boldsymbol{e}_{1}+2\boldsymbol{e}_{2}-2\boldsymbol{e}_{3}=\lambda _{2}(-5\boldsymbol{e}_{1}-6\boldsymbol{e}_{2}+4\boldsymbol{e}_{3})$，所以$\begin{cases}7 = - 5\lambda _{2},\\2 = - 6\lambda _{2},\\-2 = 4\lambda _{2}\end{cases}$，无解，所以$\overrightarrow{QR}$，$\overrightarrow{PQ}$不共线，则$P$，$Q$，$R$三点不共线；$\overrightarrow{OQ}=\overrightarrow{OP}+\overrightarrow{PQ}=-4\boldsymbol{e}_{1}-8\boldsymbol{e}_{2}+5\boldsymbol{e}_{3}$，若$\overrightarrow{OQ}//\overrightarrow{QR}$，则存在唯一实数$\lambda _{3}$使得$\overrightarrow{OQ}=\lambda _{3}\overrightarrow{QR}$，即$-4\boldsymbol{e}_{1}-8\boldsymbol{e}_{2}+5\boldsymbol{e}_{3}=\lambda _{3}(7\boldsymbol{e}_{1}+2\boldsymbol{e}_{2}-2\boldsymbol{e}_{3})$，所以$\begin{cases}-4 = 7\lambda _{3},\\-8 = 2\lambda _{3},\\5 = - 2\lambda _{3}\end{cases}$，无解，所以$\overrightarrow{OQ}$，$\overrightarrow{QR}$不共线，则$O$，$Q$，$R$三点不共线；$\overrightarrow{PR}=\overrightarrow{PQ}+\overrightarrow{QR}=2\boldsymbol{e}_{1}-4\boldsymbol{e}_{2}+2\boldsymbol{e}_{3}=2\overrightarrow{OP}$，所以$\overrightarrow{OP}//\overrightarrow{PR}$，又点$P$为两向量的公共端点，所以$O$，$P$，$R$三点共线. 故选D.

13. 下列条件，能说明空间中不重合的A，B，C三点共线的是（ ）
A. $\overrightarrow{AB}+\overrightarrow{BC}=\overrightarrow{AC}$
B. $\overrightarrow{AB}-\overrightarrow{BC}=\overrightarrow{AC}$
C. $\overrightarrow{AB}=\overrightarrow{BC}$
D. $|\overrightarrow{AB}| = |\overrightarrow{BC}|$

答案： C 【解析】对于空间中的任意向量，都有$\overrightarrow{AB}+\overrightarrow{BC}=\overrightarrow{AC}$，选项A不符合要求；若$\overrightarrow{AB}-\overrightarrow{BC}=\overrightarrow{AC}$，则$\overrightarrow{AC}+\overrightarrow{BC}=\overrightarrow{AB}$，而$\overrightarrow{AC}+\overrightarrow{CB}=\overrightarrow{AB}$，据此可知$\overrightarrow{BC}=\overrightarrow{CB}$，即$B$，$C$两点重合，选项B不符合要求；$\overrightarrow{AB}=\overrightarrow{BC}$，则$A$，$B$，$C$三点共线，选项C符合要求；$\vert\overrightarrow{AB}\vert =\vert\overrightarrow{BC}\vert$，则线段$AB$的长度与线段$BC$的长度相等，不一定有$A$，$B$，$C$三点共线，选项D不符合要求.

14. 给出下列四个命题：
①方向相反的两个向量是相反向量；
②若$\boldsymbol{a},\boldsymbol{b}$满足$|\boldsymbol{a}|＞|\boldsymbol{b}|$且$\boldsymbol{a},\boldsymbol{b}$同向，则$\boldsymbol{a}＞\boldsymbol{b}$；
③四边形ABCD是平行四边形的充要条件是$\overrightarrow{AB}=\overrightarrow{DC}$；
④对于任意向量$\boldsymbol{a},\boldsymbol{b}$，必有$|\boldsymbol{a}+\boldsymbol{b}|\leq|\boldsymbol{a}|+|\boldsymbol{b}|$.
其中正确命题的序号为_______.

答案： 3 4 【解析】对于①，长度相等且方向相反的两个向量是相反向量，故①错误；对于②，向量是不能比较大小的，故②错误；③④正确.
【易错警示】易错把向量类同于数量，导致错误的结论.

15. 对于空间中的非零向量$\overrightarrow{AB},\overrightarrow{BC},\overrightarrow{AC}$，有下列各式：
①$\overrightarrow{AB}+\overrightarrow{BC}=\overrightarrow{AC}$；
②$\overrightarrow{AB}-\overrightarrow{AC}=\overrightarrow{BC}$；
③$|\overrightarrow{AB}|+|\overrightarrow{BC}| = |\overrightarrow{AC}|$；
④$|\overrightarrow{AB}|-|\overrightarrow{AC}| = |\overrightarrow{BC}|$.
其中一定不成立的是_______.（填序号）

答案： 2 【解析】根据空间向量的加、减运算法则可知，对于①，$\overrightarrow{AB}+\overrightarrow{BC}=\overrightarrow{AC}$恒成立；对于③，当$\overrightarrow{AB}$，$\overrightarrow{BC}$，$\overrightarrow{AC}$方向相同时，有$\vert\overrightarrow{AB}\vert+\vert\overrightarrow{BC}\vert =\vert\overrightarrow{AC}\vert$；对于④，当$\overrightarrow{AB}$，$\overrightarrow{AC}$方向相同且$\overrightarrow{BC}$与$\overrightarrow{AB}$，$\overrightarrow{AC}$方向相反时，有$\vert\overrightarrow{AB}\vert-\vert\overrightarrow{AC}\vert =\vert\overrightarrow{BC}\vert$.只有②一定不成立.
【易错警示】易忽略向量共线时的特殊情形.