2024年高中必刷题高二数学选择性必修第一册人教B版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2024年高中必刷题高二数学选择性必修第一册人教B版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第17页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
1.如果一个二面角的两个半平面分别平行于另一个二面角的两个半平面,则这两个二面角的大小关系是 ( )
A.相等 B.互补
C.相等或互补 D.不能确定
A.相等 B.互补
C.相等或互补 D.不能确定
答案:
C [解析]当一个二面角的两个半平面分别平行于另一个二面角的两个半平面时,有两种情况,如图①②,则这两个二面角相等或互补


C [解析]当一个二面角的两个半平面分别平行于另一个二面角的两个半平面时,有两种情况,如图①②,则这两个二面角相等或互补


2.已知△ABC和△BCD均为边长为a的等边三角形,且AD=$\frac{\sqrt{3}}{2}$a,则二面角A−BC−D的大小为 ( )
A.30° B.45° C.60° D.90°
A.30° B.45° C.60° D.90°
答案:
C [解析]如图,取BC的中点E,连接AE,DE;

由题意得AE⊥BC,DE⊥BC,且AE = DE = $\frac{\sqrt{3}}{2}a$,
∴∠AED是二面角A - BC - D的平面角.
又
∵AD = $\frac{\sqrt{3}}{2}a$,
∴∠AED = 60°,即二面角A - BC - D的大小为60°.
C [解析]如图,取BC的中点E,连接AE,DE;

由题意得AE⊥BC,DE⊥BC,且AE = DE = $\frac{\sqrt{3}}{2}a$,
∴∠AED是二面角A - BC - D的平面角.
又
∵AD = $\frac{\sqrt{3}}{2}a$,
∴∠AED = 60°,即二面角A - BC - D的大小为60°.
3.四边形ABCD是边长为2的正方形,MA和PB 都与平面ABCD垂直,且PB=2MA=2,则平面PMD与平面ABCD所成角的余弦值为________.
答案:
$\frac{\sqrt{6}}{3}$或$\frac{\sqrt{14}}{7}$ [解析]△MPD在平面ABCD上的射影为△ABD,易得$S_{\triangle ABD}$ = 2.设平面PMD与平面ABCD所成角的大小为θ.
当M,P在平面ABCD同侧时,$S_{\triangle MPD}$ = $\sqrt{6}$,
∴$\cos\theta=\frac{S_{\triangle ABD}}{S_{\triangle MPD}}=\frac{\sqrt{6}}{3}$.
当M,P在平面ABCD异侧时,$S_{\triangle MPD}$ = $\sqrt{14}$,
∴$\cos\theta=\frac{S_{\triangle ABD}}{S_{\triangle MPD}}=\frac{\sqrt{14}}{7}$.
综上,平面PMD与平面ABCD所成角的余弦值为$\frac{\sqrt{6}}{3}$或$\frac{\sqrt{14}}{7}$.
[归纳总结]求二面角的几何方法
(1)定义法:在棱上任取一点,过这点在两个半平面内分别引棱的垂线,这两条射线所成的角,就是二面角的平面角.
(2)利用三垂线定理及其逆定理:过二面角一个面上的一点作另一个面的垂线段,再由垂足向棱作垂线得到棱上的点(即斜足),斜足与面上这一点连线和斜足与垂足连线所夹的角,就是二面角的平面角.
(3)面积射影法:$\cos\theta=\frac{S'}{S}$(其中S'表示射影图形的面积,S表示原图形的面积).
当M,P在平面ABCD同侧时,$S_{\triangle MPD}$ = $\sqrt{6}$,
∴$\cos\theta=\frac{S_{\triangle ABD}}{S_{\triangle MPD}}=\frac{\sqrt{6}}{3}$.
当M,P在平面ABCD异侧时,$S_{\triangle MPD}$ = $\sqrt{14}$,
∴$\cos\theta=\frac{S_{\triangle ABD}}{S_{\triangle MPD}}=\frac{\sqrt{14}}{7}$.
综上,平面PMD与平面ABCD所成角的余弦值为$\frac{\sqrt{6}}{3}$或$\frac{\sqrt{14}}{7}$.
[归纳总结]求二面角的几何方法
(1)定义法:在棱上任取一点,过这点在两个半平面内分别引棱的垂线,这两条射线所成的角,就是二面角的平面角.
(2)利用三垂线定理及其逆定理:过二面角一个面上的一点作另一个面的垂线段,再由垂足向棱作垂线得到棱上的点(即斜足),斜足与面上这一点连线和斜足与垂足连线所夹的角,就是二面角的平面角.
(3)面积射影法:$\cos\theta=\frac{S'}{S}$(其中S'表示射影图形的面积,S表示原图形的面积).
4.[辽宁锦州2024高二月考]已知两平面的法向量分别为m=(0,1,0),n=(0,1,1),则两平面所成的二面角为 ( )
A.45° B.135°
C.45°或135° D.120°
A.45° B.135°
C.45°或135° D.120°
答案:
C [解析]设两平面所成的二面角的平面角为θ,则$|\cos\theta| = |\cos\langle\boldsymbol{m},\boldsymbol{n}\rangle|=\frac{|\boldsymbol{m}\cdot\boldsymbol{n}|}{|\boldsymbol{m}||\boldsymbol{n}|}=\frac{\sqrt{2}}{2}$.
∵0°≤θ≤180°,
∴θ = 45°或θ = 135°.故选C.
∵0°≤θ≤180°,
∴θ = 45°或θ = 135°.故选C.
5.如图所示,在四面体P−ABC中,PC⊥平面ABC,AB=BC=CA= PC,那么二面角B−AP−C的余弦值为 ( )

A.$\frac{\sqrt{2}}{2}$ B.$\frac{\sqrt{3}}{3}$ C.$\frac{1}{7}$ D.$\frac{5}{7}$

A.$\frac{\sqrt{2}}{2}$ B.$\frac{\sqrt{3}}{3}$ C.$\frac{1}{7}$ D.$\frac{5}{7}$
答案:
C [解析]如图所示,过点B作BD⊥AP于点D,过点C作CE⊥AP于点E.
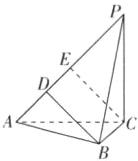
设AB = 1,则易得CE = $\frac{\sqrt{2}}{2}$,EP = $\frac{\sqrt{2}}{2}$,PA = PB = $\sqrt{2}$,所以BD = $\frac{\sqrt{14}}{4}$,ED = $\frac{\sqrt{2}}{4}$.
∵$\overrightarrow{BC}=\overrightarrow{BD}+\overrightarrow{DE}+\overrightarrow{EC}$,
∴$\overrightarrow{BC}^{2}=\overrightarrow{BD}^{2}+\overrightarrow{DE}^{2}+\overrightarrow{EC}^{2}+2\overrightarrow{BD}\cdot\overrightarrow{DE}+2\overrightarrow{DE}\cdot\overrightarrow{EC}+2\overrightarrow{EC}\cdot\overrightarrow{BD}$,
∴$\overrightarrow{EC}\cdot\overrightarrow{BD}=-\frac{1}{4}$,
∴$\cos\langle\overrightarrow{BD},\overrightarrow{EC}\rangle=-\frac{\sqrt{7}}{7}$.
又二面角B - AP - C为锐二面角,故二面角B - AP - C的余弦值为$\frac{\sqrt{7}}{7}$.
[归纳总结]求二面角的向量方法
(1)找与公共的棱垂直的方向向量法:分别在二面角的两个半平面内找到与棱垂直且以垂足为起点的两个向量,则这两个向量的夹角的大小就是二面角的大小
(2)法向量法:首先求出两个平面的法向量$\boldsymbol{m}$,$\boldsymbol{n}$,再代入公式$\cos\alpha=\pm\frac{|\boldsymbol{m}\cdot\boldsymbol{n}|}{|\boldsymbol{m}||\boldsymbol{n}|}$(其中$\boldsymbol{m}$,$\boldsymbol{n}$分别是两个平面的法向量,α是二面角的平面角)求解(注意通过观察二面角的大小选择“±”).
C [解析]如图所示,过点B作BD⊥AP于点D,过点C作CE⊥AP于点E.

设AB = 1,则易得CE = $\frac{\sqrt{2}}{2}$,EP = $\frac{\sqrt{2}}{2}$,PA = PB = $\sqrt{2}$,所以BD = $\frac{\sqrt{14}}{4}$,ED = $\frac{\sqrt{2}}{4}$.
∵$\overrightarrow{BC}=\overrightarrow{BD}+\overrightarrow{DE}+\overrightarrow{EC}$,
∴$\overrightarrow{BC}^{2}=\overrightarrow{BD}^{2}+\overrightarrow{DE}^{2}+\overrightarrow{EC}^{2}+2\overrightarrow{BD}\cdot\overrightarrow{DE}+2\overrightarrow{DE}\cdot\overrightarrow{EC}+2\overrightarrow{EC}\cdot\overrightarrow{BD}$,
∴$\overrightarrow{EC}\cdot\overrightarrow{BD}=-\frac{1}{4}$,
∴$\cos\langle\overrightarrow{BD},\overrightarrow{EC}\rangle=-\frac{\sqrt{7}}{7}$.
又二面角B - AP - C为锐二面角,故二面角B - AP - C的余弦值为$\frac{\sqrt{7}}{7}$.
[归纳总结]求二面角的向量方法
(1)找与公共的棱垂直的方向向量法:分别在二面角的两个半平面内找到与棱垂直且以垂足为起点的两个向量,则这两个向量的夹角的大小就是二面角的大小
(2)法向量法:首先求出两个平面的法向量$\boldsymbol{m}$,$\boldsymbol{n}$,再代入公式$\cos\alpha=\pm\frac{|\boldsymbol{m}\cdot\boldsymbol{n}|}{|\boldsymbol{m}||\boldsymbol{n}|}$(其中$\boldsymbol{m}$,$\boldsymbol{n}$分别是两个平面的法向量,α是二面角的平面角)求解(注意通过观察二面角的大小选择“±”).
6.[福建南平2023高二期中]在如图所示的六面体中,四边形 ADEH和BCFG均为直角梯形,A,D,C,B为直角顶点,其他四个面均为矩形,AB=BG=3,FC=4,BC=1,则平面EFGH与平面ABCD所成的锐二面角为 ( )

A.30° B.45°
C.135° D.45°或135°

A.30° B.45°
C.135° D.45°或135°
答案:
B [解析]因为四边形ADEH和BCFG均为直角梯形,A,D,C,B为直角顶点,其他四个面均为矩形,所以这个六面体是四棱柱,由题意可知DA,DC,DE两两垂直,则以点D为坐标原点建立如图所示的空间直角坐标系

则E(0,0,4),G(1,3,3),C(0,3,0),H(1,0,3),则$\overrightarrow{EH}=(1,0,-1)$,$\overrightarrow{HG}=(0,3,0)$.根据题意可知DE⊥平面ABCD,所以$\overrightarrow{DE}=(0,0,4)$即为平面ABCD的一个法向量.
设$\boldsymbol{n}=(x,y,z)$为平面EFGH的法向量,则$\begin{cases}\boldsymbol{n}\cdot\overrightarrow{EH}=x - z = 0\\\boldsymbol{n}\cdot\overrightarrow{HG}=3y = 0\end{cases}$,取x = 1,则z = 1,y = 0,则$\boldsymbol{n}=(1,0,1)$为平面EFGH的一个法向量,则$\cos\langle\boldsymbol{n},\overrightarrow{DE}\rangle=\frac{\boldsymbol{n}\cdot\overrightarrow{DE}}{|\boldsymbol{n}||\overrightarrow{DE}|}=\frac{4}{\sqrt{2}\times4}=\frac{\sqrt{2}}{2}$.
由图可知平面EFGH与平面ABCD所成的角为锐角,所以平面EFGH与平面ABCD所成的锐二面角为45°,故选B.
[多种解法一]
∵四边形ADEH与四边形BCFG均属直角梯形,A,D,C,B是直角顶点,其他面均是矩形,
∴这个六面体是四棱柱.
由题意可知DC,DE,DA两两垂直,
∴DC⊥平面EDAH.
延长EH,DA交于点M,延长FG,CB交于点N,连接MN.
由题意知DC//EF,
∴DC//平面EFGH.
又
∵平面EFGH∩平面ABCD = MN,
∴DC//MN.
∴MN⊥平面EDAH,
∴MN⊥EM,MN⊥DM,
∴∠EMD为平面EFGH与平面ABCD所成的锐二面角的平面角.
∵AH//DE,
∴$\frac{AH}{DE}=\frac{AM}{DM}$,即$\frac{3}{4}=\frac{AM}{1 + AM}$,AM = 3.
∴$\tan\angle EMD=\frac{DE}{DM}=\frac{4}{4}=1$,
∴∠EMD = 45°,即平面EFGH与平面ABCD所成的锐二面角为45°.

[多种解法二]
∵四边形ADEH与四边形BCFG均属直角梯形,A,D,C,B是直角顶点,其他面均是矩形,
∴这个六面体是四棱柱.
由题意可知DC,DE,DA两两垂直,
∴DE⊥平面ABCD.
同理HA,FC,GB都垂直于平面ABCD,
∴矩形ABCD是矩形EHGF在平面ABCD上的射影.
∴设平面EFGH与平面ABCD所成的锐二面角为α,则$\cos\alpha=\frac{S_{四边形ABCD}}{S_{四边形EHGF}}=\frac{AD\cdot AB}{EH\cdot HG}=\frac{\sqrt{2}}{2}$,
∴α = 45°.
[名师点拨]面面角与二面角有关但不同,两平面相交形成的四个二面角中的锐二面角称为面面角,所以两者的取值范围不同,平面与平面的夹角的取值范围为$[0,\frac{\pi}{2}]$,二面角的取值范围为[0,π],故面面角的余弦值为正值,法向量夹角的余弦值取绝对值即为面面角的余弦值.
若求得的二面角为锐角或直角,则面面角即为二面角;若求得的二面角为钝角,则面面角为其补角.
B [解析]因为四边形ADEH和BCFG均为直角梯形,A,D,C,B为直角顶点,其他四个面均为矩形,所以这个六面体是四棱柱,由题意可知DA,DC,DE两两垂直,则以点D为坐标原点建立如图所示的空间直角坐标系

则E(0,0,4),G(1,3,3),C(0,3,0),H(1,0,3),则$\overrightarrow{EH}=(1,0,-1)$,$\overrightarrow{HG}=(0,3,0)$.根据题意可知DE⊥平面ABCD,所以$\overrightarrow{DE}=(0,0,4)$即为平面ABCD的一个法向量.
设$\boldsymbol{n}=(x,y,z)$为平面EFGH的法向量,则$\begin{cases}\boldsymbol{n}\cdot\overrightarrow{EH}=x - z = 0\\\boldsymbol{n}\cdot\overrightarrow{HG}=3y = 0\end{cases}$,取x = 1,则z = 1,y = 0,则$\boldsymbol{n}=(1,0,1)$为平面EFGH的一个法向量,则$\cos\langle\boldsymbol{n},\overrightarrow{DE}\rangle=\frac{\boldsymbol{n}\cdot\overrightarrow{DE}}{|\boldsymbol{n}||\overrightarrow{DE}|}=\frac{4}{\sqrt{2}\times4}=\frac{\sqrt{2}}{2}$.
由图可知平面EFGH与平面ABCD所成的角为锐角,所以平面EFGH与平面ABCD所成的锐二面角为45°,故选B.
[多种解法一]
∵四边形ADEH与四边形BCFG均属直角梯形,A,D,C,B是直角顶点,其他面均是矩形,
∴这个六面体是四棱柱.
由题意可知DC,DE,DA两两垂直,
∴DC⊥平面EDAH.
延长EH,DA交于点M,延长FG,CB交于点N,连接MN.
由题意知DC//EF,
∴DC//平面EFGH.
又
∵平面EFGH∩平面ABCD = MN,
∴DC//MN.
∴MN⊥平面EDAH,
∴MN⊥EM,MN⊥DM,
∴∠EMD为平面EFGH与平面ABCD所成的锐二面角的平面角.
∵AH//DE,
∴$\frac{AH}{DE}=\frac{AM}{DM}$,即$\frac{3}{4}=\frac{AM}{1 + AM}$,AM = 3.
∴$\tan\angle EMD=\frac{DE}{DM}=\frac{4}{4}=1$,
∴∠EMD = 45°,即平面EFGH与平面ABCD所成的锐二面角为45°.

[多种解法二]
∵四边形ADEH与四边形BCFG均属直角梯形,A,D,C,B是直角顶点,其他面均是矩形,
∴这个六面体是四棱柱.
由题意可知DC,DE,DA两两垂直,
∴DE⊥平面ABCD.
同理HA,FC,GB都垂直于平面ABCD,
∴矩形ABCD是矩形EHGF在平面ABCD上的射影.
∴设平面EFGH与平面ABCD所成的锐二面角为α,则$\cos\alpha=\frac{S_{四边形ABCD}}{S_{四边形EHGF}}=\frac{AD\cdot AB}{EH\cdot HG}=\frac{\sqrt{2}}{2}$,
∴α = 45°.
[名师点拨]面面角与二面角有关但不同,两平面相交形成的四个二面角中的锐二面角称为面面角,所以两者的取值范围不同,平面与平面的夹角的取值范围为$[0,\frac{\pi}{2}]$,二面角的取值范围为[0,π],故面面角的余弦值为正值,法向量夹角的余弦值取绝对值即为面面角的余弦值.
若求得的二面角为锐角或直角,则面面角即为二面角;若求得的二面角为钝角,则面面角为其补角.
7.教材变式(多选)[重庆八中
2024高二期中]如图,已知E,F分别是正方体ABCD−A₁B₁C₁D₁ 的棱BC和CD的中点,则下列说法正确的是 ( )

A.A₁E与B₁D₁是异面直线
B.直线B₁C与EF所成角的大小为$\frac{2\pi}{3}$
C.直线A₁F与平面B₁EB所成角的正弦值为$\frac{\sqrt{3}}{3}$
D.二面角C−D₁B₁−B的余弦值为$\frac{\sqrt{6}}{3}$
2024高二期中]如图,已知E,F分别是正方体ABCD−A₁B₁C₁D₁ 的棱BC和CD的中点,则下列说法正确的是 ( )

A.A₁E与B₁D₁是异面直线
B.直线B₁C与EF所成角的大小为$\frac{2\pi}{3}$
C.直线A₁F与平面B₁EB所成角的正弦值为$\frac{\sqrt{3}}{3}$
D.二面角C−D₁B₁−B的余弦值为$\frac{\sqrt{6}}{3}$
答案:
AD [解析]对于A,因为点E∉平面A₁B₁C₁D₁,点A₁∈平面A₁B₁C₁D₁,B₁D₁⊂平面A₁B₁C₁D₁,所以A₁E与B₁D₁是异面直线,故A正确.
对于B,连接BD,由E,F分别是BC,CD的中点知,EF//BD,又B₁D₁//BD,所以EF//B₁D₁,即∠D₁B₁C或其补角为B₁C与EF所成的角,在等边三角形D₁B₁C中,∠D₁B₁C = $\frac{\pi}{3}$,故B错误.
对于C,以D为坐标原点,DA,DC,DD₁所在直线分别为x,y,z轴,建立空间直角坐标系,如图所示,
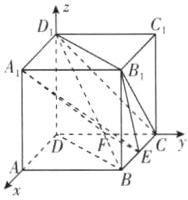
设正方体的棱长为2,则D(0,0,0),A₁(2,0,2),C(0,2,0),D₁(0,0,2),F(0,1,0),
由题意可知,平面BEB₁的法向量可取$\overrightarrow{DC}=(0,2,0)$,$\overrightarrow{A_{1}F}=(-2,1,-2)$,
设A₁F与平面B₁EB所成的角为α,则$\sin\alpha=\frac{|\overrightarrow{A_{1}F}\cdot\overrightarrow{DC}|}{|\overrightarrow{A_{1}F}||\overrightarrow{DC}|}=\frac{2}{2\times3}=\frac{1}{3}$,
所以A₁F与平面B₁EB所成角的正弦值为$\frac{1}{3}$,故C错误.
对于D,由C中坐标系可得A(2,0,0),D₁(0,0,2),B₁(2,2,2),B(2,2,0),所以$\overrightarrow{D_{1}B_{1}}=(2,2,0)$,$\overrightarrow{BB_{1}}=(0,0,2)$,$\overrightarrow{D_{1}C}=(0,2,-2)$,
设平面D₁B₁B的法向量为$\boldsymbol{m}=(x_{1},y_{1},z_{1})$,则$\begin{cases}\boldsymbol{m}\cdot\overrightarrow{D_{1}B_{1}}=2x_{1}+2y_{1}=0\\\boldsymbol{m}\cdot\overrightarrow{BB_{1}}=2z_{1}=0\end{cases}$,
令x₁ = 1,得$\boldsymbol{m}=(1,-1,0)$,
设平面D₁B₁C的法向量为$\boldsymbol{n}=(x_{2},y_{2},z_{2})$,则$\begin{cases}\boldsymbol{n}\cdot\overrightarrow{D_{1}C}=2y_{2}-2z_{2}=0\\\boldsymbol{n}\cdot\overrightarrow{D_{1}B_{1}}=2x_{2}+2y_{2}=0\end{cases}$,令y₂ = - 1,可得$\boldsymbol{n}=(1,-1,-1)$,
则$\cos\langle\boldsymbol{m},\boldsymbol{n}\rangle=\frac{\boldsymbol{m}\cdot\boldsymbol{n}}{|\boldsymbol{m}||\boldsymbol{n}|}=\frac{2}{\sqrt{2}\times\sqrt{3}}=\frac{\sqrt{6}}{3}$,又因为二面角C - D₁B₁ - B的平面角为锐角,所以二面角C - D₁B₁ - B的余弦值为$\frac{\sqrt{6}}{3}$,故D正确. 故选AD.
[链接教材]本题是教材P67第4题的变式与延伸,较为全面地考查了利用空间向量解决立体几何中的度量问题,不管几何体的结构如何变化,利用空间向量求空间角的方法不变.
AD [解析]对于A,因为点E∉平面A₁B₁C₁D₁,点A₁∈平面A₁B₁C₁D₁,B₁D₁⊂平面A₁B₁C₁D₁,所以A₁E与B₁D₁是异面直线,故A正确.
对于B,连接BD,由E,F分别是BC,CD的中点知,EF//BD,又B₁D₁//BD,所以EF//B₁D₁,即∠D₁B₁C或其补角为B₁C与EF所成的角,在等边三角形D₁B₁C中,∠D₁B₁C = $\frac{\pi}{3}$,故B错误.
对于C,以D为坐标原点,DA,DC,DD₁所在直线分别为x,y,z轴,建立空间直角坐标系,如图所示,

设正方体的棱长为2,则D(0,0,0),A₁(2,0,2),C(0,2,0),D₁(0,0,2),F(0,1,0),
由题意可知,平面BEB₁的法向量可取$\overrightarrow{DC}=(0,2,0)$,$\overrightarrow{A_{1}F}=(-2,1,-2)$,
设A₁F与平面B₁EB所成的角为α,则$\sin\alpha=\frac{|\overrightarrow{A_{1}F}\cdot\overrightarrow{DC}|}{|\overrightarrow{A_{1}F}||\overrightarrow{DC}|}=\frac{2}{2\times3}=\frac{1}{3}$,
所以A₁F与平面B₁EB所成角的正弦值为$\frac{1}{3}$,故C错误.
对于D,由C中坐标系可得A(2,0,0),D₁(0,0,2),B₁(2,2,2),B(2,2,0),所以$\overrightarrow{D_{1}B_{1}}=(2,2,0)$,$\overrightarrow{BB_{1}}=(0,0,2)$,$\overrightarrow{D_{1}C}=(0,2,-2)$,
设平面D₁B₁B的法向量为$\boldsymbol{m}=(x_{1},y_{1},z_{1})$,则$\begin{cases}\boldsymbol{m}\cdot\overrightarrow{D_{1}B_{1}}=2x_{1}+2y_{1}=0\\\boldsymbol{m}\cdot\overrightarrow{BB_{1}}=2z_{1}=0\end{cases}$,
令x₁ = 1,得$\boldsymbol{m}=(1,-1,0)$,
设平面D₁B₁C的法向量为$\boldsymbol{n}=(x_{2},y_{2},z_{2})$,则$\begin{cases}\boldsymbol{n}\cdot\overrightarrow{D_{1}C}=2y_{2}-2z_{2}=0\\\boldsymbol{n}\cdot\overrightarrow{D_{1}B_{1}}=2x_{2}+2y_{2}=0\end{cases}$,令y₂ = - 1,可得$\boldsymbol{n}=(1,-1,-1)$,
则$\cos\langle\boldsymbol{m},\boldsymbol{n}\rangle=\frac{\boldsymbol{m}\cdot\boldsymbol{n}}{|\boldsymbol{m}||\boldsymbol{n}|}=\frac{2}{\sqrt{2}\times\sqrt{3}}=\frac{\sqrt{6}}{3}$,又因为二面角C - D₁B₁ - B的平面角为锐角,所以二面角C - D₁B₁ - B的余弦值为$\frac{\sqrt{6}}{3}$,故D正确. 故选AD.
[链接教材]本题是教材P67第4题的变式与延伸,较为全面地考查了利用空间向量解决立体几何中的度量问题,不管几何体的结构如何变化,利用空间向量求空间角的方法不变.
8.[辽宁鞍山一中2024高二期中]已知四棱锥P−ABCD的底面ABCD为菱形,且∠DAB=60°,PD⊥AD.
(1)证明:PB=PC;
(2)若PD=PB=BC=2$\sqrt{3}$,求二面角A−PB−C 的余弦值.

(1)证明:PB=PC;
(2)若PD=PB=BC=2$\sqrt{3}$,求二面角A−PB−C 的余弦值.

答案:
(1)[证明]取BC中点E,连接BD,DE,PE,如图,

因为底面ABCD为菱形,且∠DAB = 60°,所以△BCD为等边三角形,故DE⊥BC,因为PD⊥AD,AD//BC,所以PD⊥BC. 又因为PD∩DE = D,PD,DE⊂平面PDE,所以BC⊥平面PDE,又PE⊂平面PDE,所以BC⊥PE. 又因为E是BC的中点,所以PB = PC.
(2)[解]因为DA//BC,所以DA⊥DE,所以以D为坐标原点,DA,DE所在直线分别为x轴、y轴,过D作垂直于平面ABCD的直线为z轴,建立如图所示的空间直角坐标系Dxyz,

过P作PF⊥DE于点F,又PF⊂平面PDE,则PF⊥BC,DE∩BC = E,DE,BC⊂平面BCD,
所以PF⊥平面BCD,由PD = PB = BC = 2$\sqrt{3}$得A(2$\sqrt{3}$,0,0),B($\sqrt{3}$,3,0),C(-$\sqrt{3}$,3,0),所以$\overrightarrow{AB}=(-\sqrt{3},3,0)$,$\overrightarrow{BC}=(-2\sqrt{3},0,0)$,
因为P - BCD为正四面体,所以F为等边三角形BCD的中心,所以F(0,2,0),P(0,2,2$\sqrt{2}$),所以$\overrightarrow{PB}=(\sqrt{3},1,-2\sqrt{2})$.
设平面PAB的法向量为$\boldsymbol{m}=(x_{1},y_{1},z_{1})$,则$\begin{cases}\boldsymbol{m}\cdot\overrightarrow{AB}=0\\\boldsymbol{m}\cdot\overrightarrow{PB}=0\end{cases}$,即$\begin{cases}-\sqrt{3}x_{1}+3y_{1}=0\\\sqrt{3}x_{1}+y_{1}-2\sqrt{2}z_{1}=0\end{cases}$,
令x₁ = $\sqrt{3}$,则y₁ = 1,z₁ = $\sqrt{2}$,则$\boldsymbol{m}=(\sqrt{3},1,\sqrt{2})$.
设平面PBC的法向量为$\boldsymbol{n}=(x_{2},y_{2},z_{2})$,则$\begin{cases}\boldsymbol{n}\cdot\overrightarrow{BC}=0\\\boldsymbol{n}\cdot\overrightarrow{PB}=0\end{cases}$,
即$\begin{cases}-2\sqrt{3}x_{2}=0\\\sqrt{3}x_{2}+y_{2}-2\sqrt{2}z_{2}=0\end{cases}$,令z₂ = 1,可得平面PBC的一个法向量为$\boldsymbol{n}=(0,2\sqrt{2},1)$,则$\cos\langle\boldsymbol{m},\boldsymbol{n}\rangle=\frac{\boldsymbol{m}\cdot\boldsymbol{n}}{|\boldsymbol{m}||\boldsymbol{n}|}=\frac{3\sqrt{2}}{\sqrt{6}\times3}=\frac{1}{\sqrt{3}}=\frac{\sqrt{3}}{3}$.
又二面角A - PB - C的平面角为钝角,所以二面角A - PB - C的余弦值为$-\frac{\sqrt{3}}{3}$.
(1)[证明]取BC中点E,连接BD,DE,PE,如图,

因为底面ABCD为菱形,且∠DAB = 60°,所以△BCD为等边三角形,故DE⊥BC,因为PD⊥AD,AD//BC,所以PD⊥BC. 又因为PD∩DE = D,PD,DE⊂平面PDE,所以BC⊥平面PDE,又PE⊂平面PDE,所以BC⊥PE. 又因为E是BC的中点,所以PB = PC.
(2)[解]因为DA//BC,所以DA⊥DE,所以以D为坐标原点,DA,DE所在直线分别为x轴、y轴,过D作垂直于平面ABCD的直线为z轴,建立如图所示的空间直角坐标系Dxyz,

过P作PF⊥DE于点F,又PF⊂平面PDE,则PF⊥BC,DE∩BC = E,DE,BC⊂平面BCD,
所以PF⊥平面BCD,由PD = PB = BC = 2$\sqrt{3}$得A(2$\sqrt{3}$,0,0),B($\sqrt{3}$,3,0),C(-$\sqrt{3}$,3,0),所以$\overrightarrow{AB}=(-\sqrt{3},3,0)$,$\overrightarrow{BC}=(-2\sqrt{3},0,0)$,
因为P - BCD为正四面体,所以F为等边三角形BCD的中心,所以F(0,2,0),P(0,2,2$\sqrt{2}$),所以$\overrightarrow{PB}=(\sqrt{3},1,-2\sqrt{2})$.
设平面PAB的法向量为$\boldsymbol{m}=(x_{1},y_{1},z_{1})$,则$\begin{cases}\boldsymbol{m}\cdot\overrightarrow{AB}=0\\\boldsymbol{m}\cdot\overrightarrow{PB}=0\end{cases}$,即$\begin{cases}-\sqrt{3}x_{1}+3y_{1}=0\\\sqrt{3}x_{1}+y_{1}-2\sqrt{2}z_{1}=0\end{cases}$,
令x₁ = $\sqrt{3}$,则y₁ = 1,z₁ = $\sqrt{2}$,则$\boldsymbol{m}=(\sqrt{3},1,\sqrt{2})$.
设平面PBC的法向量为$\boldsymbol{n}=(x_{2},y_{2},z_{2})$,则$\begin{cases}\boldsymbol{n}\cdot\overrightarrow{BC}=0\\\boldsymbol{n}\cdot\overrightarrow{PB}=0\end{cases}$,
即$\begin{cases}-2\sqrt{3}x_{2}=0\\\sqrt{3}x_{2}+y_{2}-2\sqrt{2}z_{2}=0\end{cases}$,令z₂ = 1,可得平面PBC的一个法向量为$\boldsymbol{n}=(0,2\sqrt{2},1)$,则$\cos\langle\boldsymbol{m},\boldsymbol{n}\rangle=\frac{\boldsymbol{m}\cdot\boldsymbol{n}}{|\boldsymbol{m}||\boldsymbol{n}|}=\frac{3\sqrt{2}}{\sqrt{6}\times3}=\frac{1}{\sqrt{3}}=\frac{\sqrt{3}}{3}$.
又二面角A - PB - C的平面角为钝角,所以二面角A - PB - C的余弦值为$-\frac{\sqrt{3}}{3}$.
9.[湖北武汉华师大一附中2024高二月考]如图,在正方体ABEF−DCE'F'中,M,N分别为AC,BF的中点,则平面MNA与平面MNB的夹角的余弦值为 ( )
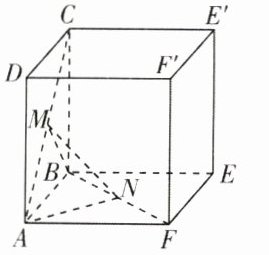
A.−$\frac{1}{3}$ B.$\frac{1}{3}$ C.−$\frac{2\sqrt{2}}{3}$ D.$\frac{2\sqrt{2}}{3}$

A.−$\frac{1}{3}$ B.$\frac{1}{3}$ C.−$\frac{2\sqrt{2}}{3}$ D.$\frac{2\sqrt{2}}{3}$
答案:
B [解析]设正方体的棱长为1,以B为坐标原点,BA,BE,BC所在直线分别为x轴、y轴、z轴建立空间直角坐标系Bxyz,如图所示,则M($\frac{1}{2}$,0,$\frac{1}{2}$),N($\frac{1}{2}$,$\frac{1}{2}$,0),A(1,0,0),B(0,0,0).
设平面AMN的法向量为$\boldsymbol{n}_{1}=(x,y,z)$,由于$\overrightarrow{AM}=(-\frac{1}{2},0,\frac{1}{2})$,$\overrightarrow{AN}=(-\frac{1}{2},\frac{1}{2},0)$,则$\begin{cases}\boldsymbol{n}_{1}\cdot\overrightarrow{AM}=0\\\boldsymbol{n}_{1}\cdot\overrightarrow{AN}=0\end{cases}$,
即$\begin{cases}-\frac{1}{2}x+\frac{1}{2}z=0\\-\frac{1}{2}x+\frac{1}{2}y=0\end{cases}$,
令x = 1,解得y = 1,z = 1,于是$\boldsymbol{n}_{1}=(1,1,1)$,
同理可求得平面BMN的一个法向量为$\boldsymbol{n}_{2}=(1,-1,-1)$,所以$\cos\langle\boldsymbol{n}_{1},\boldsymbol{n}_{2}\rangle=\frac{\boldsymbol{n}_{1}\cdot\boldsymbol{n}_{2}}{|\boldsymbol{n}_{1}||\boldsymbol{n}_{2}|}=\frac{-1}{\sqrt{3}\times\sqrt{3}}=-\frac{1}{3}$,
设平面MNA与平面MNB的夹角为θ,则$\cos\theta=|\cos\langle\boldsymbol{n}_{1},\boldsymbol{n}_{2}\rangle|=\frac{1}{3}$. 故所求两平面夹角的余弦值为$\frac{1}{3}$. 故选B.
[易错警示]面面夹角是平面α与平面β相交形成的四个二面角中不大于$\frac{\pi}{2}$的二面角,故面面夹角θ∈$[0,\frac{\pi}{2}]$,因此面面夹角的余弦值一定不小于0,故两平面法向量夹角的余弦值的绝对值就是两平面夹角的余弦值,不用分情况讨论面面夹角是锐角还是钝角,注意和二面角进行区分.
设平面AMN的法向量为$\boldsymbol{n}_{1}=(x,y,z)$,由于$\overrightarrow{AM}=(-\frac{1}{2},0,\frac{1}{2})$,$\overrightarrow{AN}=(-\frac{1}{2},\frac{1}{2},0)$,则$\begin{cases}\boldsymbol{n}_{1}\cdot\overrightarrow{AM}=0\\\boldsymbol{n}_{1}\cdot\overrightarrow{AN}=0\end{cases}$,
即$\begin{cases}-\frac{1}{2}x+\frac{1}{2}z=0\\-\frac{1}{2}x+\frac{1}{2}y=0\end{cases}$,
令x = 1,解得y = 1,z = 1,于是$\boldsymbol{n}_{1}=(1,1,1)$,
同理可求得平面BMN的一个法向量为$\boldsymbol{n}_{2}=(1,-1,-1)$,所以$\cos\langle\boldsymbol{n}_{1},\boldsymbol{n}_{2}\rangle=\frac{\boldsymbol{n}_{1}\cdot\boldsymbol{n}_{2}}{|\boldsymbol{n}_{1}||\boldsymbol{n}_{2}|}=\frac{-1}{\sqrt{3}\times\sqrt{3}}=-\frac{1}{3}$,
设平面MNA与平面MNB的夹角为θ,则$\cos\theta=|\cos\langle\boldsymbol{n}_{1},\boldsymbol{n}_{2}\rangle|=\frac{1}{3}$. 故所求两平面夹角的余弦值为$\frac{1}{3}$. 故选B.
[易错警示]面面夹角是平面α与平面β相交形成的四个二面角中不大于$\frac{\pi}{2}$的二面角,故面面夹角θ∈$[0,\frac{\pi}{2}]$,因此面面夹角的余弦值一定不小于0,故两平面法向量夹角的余弦值的绝对值就是两平面夹角的余弦值,不用分情况讨论面面夹角是锐角还是钝角,注意和二面角进行区分.
查看更多完整答案,请扫码查看


