《2024年高中必刷题高二数学选择性必修第一册人教B版》

1. [重庆第一中学2023高二期中]已知直线$l_1$：$x - 2y = 0$，$l_2$：$2x - y = 0$，若双曲线$C$与$l_1$，$l_2$均无公共点，则$C$的方程可以是 （ ）
A. $\frac{x^{2}}{3}-\frac{y^{2}}{2}=1$
B. $\frac{x^{2}}{4}-\frac{y^{2}}{3}=1$
C. $\frac{y^{2}}{8}-\frac{x^{2}}{2}=1$
D. $\frac{y^{2}}{3}-\frac{x^{2}}{2}=1$

答案： C 【解析】直线$l_1$，$l_2$的斜率分别是$k_1=\frac{1}{2}$，$k_2 = 2$。
对A：该双曲线是焦点在$x$轴上的双曲线，其过第一象限的渐近线的方程为$y=\frac{\sqrt{6}}{3}x$，又$k_1＜\frac{\sqrt{6}}{3}＜k_2$，故曲线$C$与直线$l_1$有两个公共点，不满足题意，A错误；
对B：该双曲线是焦点在$x$轴上的双曲线，其过第一象限的渐近线的方程为$y=\frac{\sqrt{3}}{2}x$，又$k_1＜\frac{\sqrt{3}}{2}＜k_2$，故双曲线$C$与直线$l_1$有两个公共点，不满足题意，B错误；
对C：该双曲线是焦点在$y$轴上的双曲线，其过第一象限的渐近线的方程为$y = 2x$，又$k_1＜k_2 = 2$，故双曲线$C$与直线$l_1$，$l_2$都没有公共点，满足题意，C正确；
对D：该双曲线是焦点在$y$轴上的双曲线，其过第一象限的渐近线的方程为$y=\frac{\sqrt{6}}{2}x$，又$k_1＜\frac{\sqrt{6}}{2}＜k_2$，故双曲线$C$与直线$l_2$有两个公共点，不满足题意，D错误。故选C。

2. (多选) [湖北武汉三中2024高二月考]已知$F$是抛物线$C$：$y^{2}=8x$的焦点，过点$F$作两条互相垂直的直线$l_1$，$l_2$，$l_1$与$C$相交于$A$，$B$两点，$l_2$与$C$相交于$E$，$D$两点，直线$l$为抛物线$C$的准线，则 （ ）
A. $\angle AOB$有可能为锐角
B. 以$|AB|$为直径的圆与$l$相切
C. $|AB|+|DE|$的最小值为32
D. $\triangle AEF$和$\triangle BFD$面积之和的最小值为32

答案：
BCD 【解析】由$C:y^2 = 8x$，故焦点坐标为$F(2,0)$，准线方程为$l:x = - 2$。

设$l_1:x = my + 2(m\neq0)$，$A(x_1,y_1)$，$B(x_2,y_2)$，$D(x_3,y_3)$，$E(x_4,y_4)$，
则$l_2:x=-\frac{1}{m}y + 2$。
联立$\begin{cases}x = my + 2\\y^2 = 8x\end{cases}$，消去$x$得$y^2 - 8my - 16 = 0$，$\Delta = 64m^2 + 64＞0$，
有$y_1 + y_2 = 8m$，$y_1y_2 = - 16$，
则$\overrightarrow{OA}\cdot\overrightarrow{OB}=x_1x_2 + y_1y_2=\frac{(y_1y_2)^2}{64}+y_1y_2 = 4 - 16 = - 12＜0$，
故$\angle AOB$恒为钝角，故A错误。
设线段$AB$的中点为$M$，由题可得点$M$的坐标为$(\frac{x_1 + x_2}{2},\frac{y_1 + y_2}{2})$，
$\frac{x_1 + x_2}{2}=\frac{m(y_1 + y_2)+4}{2}=4m^2 + 2$，
故$M(4m^2 + 2,4m)$，
$|AB|=x_1 + x_2 + p = 8m^2 + 8$，
则以$|AB|$为直径的圆是以$M(4m^2 + 2,4m)$为圆心，$4m^2 + 4$为半径，
圆心$M(4m^2 + 2,4m)$到$l:x = - 2$的距离为$4m^2 + 4$，与半径相等，故以$|AB|$为直径的圆与$l$相切，故B正确。
由B中分析得$|AB|=x_1 + x_2 + p = 8m^2 + 8$，
同理可得$|DE|=8(-\frac{1}{m})^2 + 8=\frac{8}{m^2}+8$，
即$|AB|+|DE|=8m^2 + 8+\frac{8}{m^2}+8\geq16 + 2\sqrt{8m^2\cdot\frac{8}{m^2}} = 32$，当且仅当$m=\pm1$时，等号成立，故C正确。
$S_{\triangle AEF}+S_{\triangle BFD}=\frac{1}{2}(|AF|\cdot|EF|+|BF|\cdot|DF|)=\frac{1}{2}[(x_1 + 2)(x_4 + 2)+(x_2 + 2)(x_3 + 2)]=\frac{1}{2}(x_1x_4 + x_2x_3 + 2x_1 + 2x_2 + 2x_3 + 2x_4 + 8)=\frac{1}{2}(x_1x_4 + x_2x_3 + 16m^2+\frac{16}{m^2}+24)$，
由$x_1x_2=\frac{(y_1y_2)^2}{64}=4$，得$x_2=\frac{4}{x_1}$，
同理可得$x_4=\frac{4}{x_3}$，
即$S_{\triangle AEF}+S_{\triangle BFD}=\frac{1}{2}(x_1x_4 + x_2x_3 + 16m^2+\frac{16}{m^2}+24)=\frac{1}{2}(\frac{4x_1}{x_3}+\frac{4x_3}{x_1}+16m^2+\frac{16}{m^2}+24)\geq\frac{1}{2}(2\sqrt{\frac{4x_1}{x_3}\cdot\frac{4x_3}{x_1}}+2\sqrt{16m^2\cdot\frac{16}{m^2}}+24)=32$，
当且仅当$m = \pm1$，$x_1 = x_3$时等号成立，
当$m=\pm1$时，由抛物线的对称性及直线的对称性可得$x_1 = x_3$，即$m=\pm1$，$x_1 = x_3$可同时取等，故D正确。故选BCD。

3. [山东青岛2024高二期中]已知双曲线$C$：$\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1(a＞0,b＞0)$的右焦点为$F(2,0)$，且$C$的一条渐近线恰好与直线$x - y + 1 = 0$垂直.
(1)求$C$的方程；
(2)直线$l$：$x = my + 1$与$C$的右支交于$A$，$B$两点，点$D$在$C$上，且$AD\perp x$轴，求证：直线$BD$过点$F$.

答案：

(1)【解】由焦点坐标为$F(2,0)$得$c = 2$，所以$a^2 + b^2 = 2^2$，
由双曲线$C:\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a＞0,b＞0)$的一条渐近线恰好与直线$x - y + 1 = 0$垂直，
得$-\frac{b}{a}=-1$，即$\frac{b}{a}=1$，所以$a^2 = b^2 = 2$，
所以双曲线$C$的方程为$\frac{x^2}{2}-\frac{y^2}{2}=1$，即$x^2 - y^2 = 2$。
(2)【证明】由题意可知直线$l$的斜率存在且不为$0$，所以$m\neq0$。
设$A(x_1,y_1)$，$B(x_2,y_2)$，则$D(x_1,-y_1)$，由
(1)可知，双曲线$C$的渐近线为$y=\pm x$，
又直线$l$与双曲线$C$的右支交于$A$，$B$两点，则$\frac{1}{|m|}＞1$，即$0＜|m|＜1$。
联立$\begin{cases}x = my + 1\\x^2 - y^2 = 2\end{cases}$，消去$x$得$(m^2 - 1)y^2 + 2my - 1 = 0$，
$\Delta = 4m^2 + 4(m^2 - 1)=4(2m^2 - 1)＞0$，得$\frac{\sqrt{2}}{2}＜|m|＜1$，
则$y_1 + y_2 = -\frac{2m}{m^2 - 1}$，$y_1y_2 = -\frac{1}{m^2 - 1}$，则$y_1 + y_2 = 2my_1y_2$。
因为$F(2,0)$，所以$\overrightarrow{FB}=(x_2 - 2,y_2)$，$\overrightarrow{FD}=(x_1 - 2,-y_1)$，
所以$(x_1 - 2)y_2+(x_2 - 2)y_1=(my_1 - 1)y_2+(my_2 - 1)y_1 = 2my_1y_2-(y_1 + y_2)=0$，所以$\overrightarrow{FB}//\overrightarrow{FD}$，又$\overrightarrow{FB}$，$\overrightarrow{FD}$有公共点$F$，所以$B$，$F$，$D$三点共线，
所以直线$BD$过点$F$。

4. [河南开封五县2024高二期中联考]已知椭圆$E$：$\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1(a＞b＞0)$的左、右顶点分别为$C$，$D$，且焦距为2，$F$为椭圆的右焦点，点$M$在椭圆上且异于$C$，$D$两点，且直线$MC$与$MD$的斜率之积为$-\frac{3}{4}$.
(1)求椭圆$E$的标准方程；
(2)过点$P(4,0)$作一条斜率不为0的直线与椭圆$E$相交于$A$，$B$两点（$A$在$B$，$P$之间），直线$BF$与椭圆$E$的另一个交点为$H$，求证：点$A$，$H$关于$x$轴对称.

答案：

(1)【解】由题意有$C(-a,0)$，$D(a,0)$，设$M(x,y)(x\neq\pm a)$，
则$k_{MC}\cdot k_{MD}=\frac{y}{x + a}\cdot\frac{y}{x - a}=-\frac{3}{4}$，化简得$\frac{x^2}{a^2}+\frac{4y^2}{3a^2}=1$，结合$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$，可得$b^2=\frac{3}{4}a^2$，
由椭圆焦距为$2$，得$c = 1$，所以$a^2 - b^2 = a^2-\frac{3}{4}a^2=\frac{1}{4}a^2 = 1$，所以$a^2 = 4$，$b^2 = 3$，
则椭圆$E$的标准方程为$\frac{x^2}{4}+\frac{y^2}{3}=1$。
(2)【证明】显然直线$AB$的斜率不存在时，与椭圆无交点，
根据椭圆的对称性，欲证点$A$，$H$关于$x$轴对称，
只需证$k_{FA}=-k_{FH}$，即证$k_{FA}+k_{FH}=0$。

设$A(x_2,y_2)$，$B(x_1,y_1)$，直线$AB$的方程为$x = my + 4$，$m\neq0$。
由$\begin{cases}x = my + 4\\3x^2 + 4y^2 = 12\end{cases}$，消去$x$得$(3m^2 + 4)y^2 + 24my + 36 = 0$，
$\Delta=(24m)^2 - 4\times36(3m^2 + 4)＞0$，解得$m^2＞4$，
所以$y_1 + y_2 = -\frac{24m}{3m^2 + 4}$，$y_1y_2 = \frac{36}{3m^2 + 4}$，
则$k_{FA}+k_{FH}=\frac{y_2}{x_2 - 1}+\frac{y_1}{x_1 - 1}=\frac{y_1x_2 + y_2x_1-(y_1 + y_2)}{(x_1 - 1)(x_2 - 1)}$。
因为$y_1x_2 + y_2x_1-(y_1 + y_2)=2my_1y_2 + 3(y_1 + y_2)=2m\cdot\frac{36}{3m^2 + 4}+3\cdot\frac{-24m}{3m^2 + 4}=0$，所以$k_{FA}+k_{FH}=0$，即点$A$，$H$关于$x$轴对称。
【规律方法】对于直线与圆锥曲线问题的求解策略
(1)研究直线与圆锥曲线位置关系，一般转化为研究直线方程与圆锥曲线方程组成的方程组解的问题，结合一元二次方程的根与系数的关系，转化为方程的性质进行求解；
(2)对于直线与圆锥曲线的客观题，解答时注意图形的几何性质的应用，利用数形结合思想求解，有时更加方便；
(3)合理应用“设而不求”法，在“设而不求”的技巧中，要注意运算的合理性、目的性，同时合理应用根与系数的关系、中点坐标公式、向量平行与垂直关系等，使得思路更加清晰，运算得以简化，从而迅速地解决问题。

5. [天津南开中学2023高二月考]已知斜率存在的直线$l$与椭圆$\frac{x^{2}}{16}+\frac{y^{2}}{4}=1$交于$A$，$B$两点，且$l$与圆$C$：$(x - 1)^{2}+y^{2}=1$相切于点$P$.若$P$为线段$AB$的中点，则直线$PC$的斜率为 （ ）
A. $2\sqrt{2}$
B. $-\sqrt{2}$
C. $2\sqrt{2}$或$-2\sqrt{2}$
D. $\sqrt{2}$或$-\sqrt{2}$

答案： C 【解析】设点$A$，$B$，$P$的坐标分别为$(x_1,y_1)$，$(x_2,y_2)$，$(m,n)$，则$\frac{x_1^2}{16}+\frac{y_1^2}{4}=1$，$\frac{x_2^2}{16}+\frac{y_2^2}{4}=1$，两式作差可得$\frac{y_1 + y_2}{2}\times\frac{y_1 - y_2}{x_1 - x_2}=-\frac{1}{4}$，即$\frac{n}{m}\times\frac{y_1 - y_2}{x_1 - x_2}=-\frac{1}{4}$。
因为直线$PC$与直线$AB$垂直，故可得$\frac{n}{m - 1}\times\frac{y_1 - y_2}{x_1 - x_2}=-1$，与$\frac{n}{m}\times\frac{y_1 - y_2}{x_1 - x_2}=-\frac{1}{4}$联立后可得$\frac{m}{m - 1}=4$，解得$m=\frac{4}{3}$。
又因为点$P$在圆$C$上，故可得$(m - 1)^2 + n^2 = 1$，解得$n=\pm\frac{2\sqrt{2}}{3}$，则$\frac{n}{m - 1}=\pm2\sqrt{2}$，即直线$CP$的斜率为$2\sqrt{2}$或$-2\sqrt{2}$。故选C。

6. [河南省实验中学2024高二月考]已知双曲线$C$：$\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1(a＞0,b＞0)$的右焦点为$F$，虚轴的上端点为$B$，点$P$，$Q$为$C$上两点，点$M(-2,1)$为弦$PQ$的中点，且$PQ// BF$，记双曲线的离心率为$e$，则$e^{2}=$_______.

答案： $\frac{\sqrt{2}+1}{2}$ 【解析】由题意知$F(c,0)$，$B(0,b)$，则$k_{PQ}=k_{BF}=-\frac{b}{c}$。设$P(x_1,y_1)$，$Q(x_2,y_2)$，则$\begin{cases}\frac{x_1^2}{a^2}-\frac{y_1^2}{b^2}=1\\\frac{x_2^2}{a^2}-\frac{y_2^2}{b^2}=1\end{cases}$两式相减得$\frac{y_1 - y_2}{x_1 - x_2}=\frac{b^2(x_1 + x_2)}{a^2(y_1 + y_2)}$。因为$PQ$的中点为$M(-2,1)$，所以$x_1 + x_2=-4$，$y_1 + y_2 = 2$，又$k_{PQ}=\frac{y_1 - y_2}{x_1 - x_2}=-\frac{b}{c}$，所以$-\frac{b}{c}=-\frac{4b^2}{2a^2}$，整理得$a^2 = 2bc$，所以$a^4 = 4b^2c^2 = 4c^2(c^2 - a^2)$，得$4e^4 - 4e^2 - 1 = 0$，解得$e^2=\frac{\sqrt{2}+1}{2}$(负根舍去)。
【多种解法】由题意知$F(c,0)$，$B(0,b)$，则$k_{BF}=-\frac{b}{c}$。易得直线$PQ$的斜率存在且不为$0$，则设直线$PQ$的方程为$y - 1 = k(x + 2)$，即$y = kx + 2k + 1$，与双曲线方程联立得$(b^2 - a^2k^2)x^2 - 2a^2k(2k + 1)x - a^2(2k + 1)^2 - a^2b^2 = 0$，$\Delta＞0$。设$P(x_1,y_1)$，$Q(x_2,y_2)$，结合$M(-2,1)$为$PQ$的中点，得$x_1 + x_2=\frac{2a^2k(2k + 1)}{b^2 - a^2k^2}=-4$。
又$k = k_{BF}=-\frac{b}{c}$，所以$2a^2\cdot(-\frac{b}{c})[2\cdot(-\frac{b}{c})+1]=-4b^2 + 4a^2\cdot(-\frac{b}{c})^2$，整理得$a^2 = 2bc$，所以$a^4 = 4b^2c^2 = 4c^2(c^2 - a^2)$，得$4e^4 - 4e^2 - 1 = 0$，得$e^2=\frac{\sqrt{2}+1}{2}$(负根舍去)。

7. [陕西咸阳2024高二质量检测]已知抛物线$C$：$y^{2}=2px(p＞0)$上的点$M(5,m)$到焦点$F$的距离为6.
(1)求抛物线$C$的方程；
(2)过点$P(2,1)$作直线$l$交抛物线$C$于$A$，$B$两点，且点$P$是线段$AB$的中点，求直线$l$的方程.

答案：
(1)【解】由题设，抛物线的准线方程为$x = -\frac{p}{2}$，$\therefore$由抛物线定义知$5+\frac{p}{2}=6$，可得$p = 2$，$\therefore C:y^2 = 4x$。
(2)由题设可知，直线$l$的斜率存在且不为$0$，设$l:x = k(y - 1)+2$，$k\neq0$，联立抛物线方程，得$y^2 = 4k(y - 1)+8$，整理得$y^2 - 4ky + 4k - 8 = 0$，则$y_A + y_B = 4k$，又$P$是线段$AB$的中点，
$\therefore 4k = 2$，即$k=\frac{1}{2}$，故$l:2x - y - 3 = 0$。

8. [黑龙江哈尔滨九中2024高二期中]已知点$A(-2,0)$，$B(2,0)$，直线$AM$，$BM$相交于点$M$，且它们的斜率之积是3.
(1)求点$M$的轨迹$C$的方程.
(2)过点$N(2,3)$能否作一条直线$m$与轨迹$C$交于两点$P$，$Q$，且点$N$是线段$PQ$的中点？若能，求出直线$m$的方程；若不能，说明理由.

答案：

(1)【解】设$M(x,y)$，$x\neq\pm2$。
$\because k_{AM}=\frac{y - 0}{x + 2}$，$k_{BM}=\frac{y - 0}{x - 2}$，$k_{AM}\cdot k_{BM}=3$，
$\therefore\frac{y - 0}{x + 2}\cdot\frac{y - 0}{x - 2}=3$，整理得$3x^2 - y^2 =$

9. 已知抛物线$y^{2}=4x$，过焦点$F$作直线与抛物线交于点$A$，$B$（点$A$在$x$轴下方），点$A_1$与点$A$关于$x$轴对称. 若直线$AB$的斜率为1，则直线$A_1B$的斜率为 （ ）
A. $\frac{\sqrt{3}}{3}$
B. $\sqrt{3}$
C. $\frac{\sqrt{2}}{2}$
D. $\sqrt{2}$

答案：

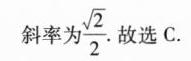
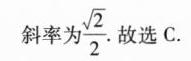
10. 已知椭圆$C$：$\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1(a＞b＞0)$的离心率$e = \frac{\sqrt{2}}{2}$，点$P(-\sqrt{2},1)$在该椭圆上.
(1)求椭圆$C$的方程；
(2)若$A$，$B$是椭圆$C$上关于直线$y = kx + 1$对称的两点，求实数$k$的取值范围.

答案：