2024年高中必刷题高二数学选择性必修第一册人教B版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2024年高中必刷题高二数学选择性必修第一册人教B版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第38页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
1. 直线$l_1:x - my - 2 = 0$与直线$l_2:mx + y + 2 = 0$交于点$Q$,$m$是实数,$O$为坐标原点,则$|OQ|$的最大值是( )
A. 2
B. $2\sqrt{2}$
C. $2\sqrt{3}$
D. 4
A. 2
B. $2\sqrt{2}$
C. $2\sqrt{3}$
D. 4
答案:
B
2. [四川成都2024高二月考]已知点$A(-4,0)$,$B(0,-3)$,点$P(x,y)$在线段$AB$(含端点)上移动,则$\sqrt{(x - 4)^2 + y^2}$的最小值为________.
答案:


3. (多选)[江西抚州一中2024高二月考]2023年动画电影《长安三万里》重新点燃了人们对唐诗的热情,唐诗中边塞诗又称出塞诗,是唐代汉族诗歌的主要题材,是唐诗当中思想性最深刻、想象力最丰富、艺术性最强的一部分,唐代诗人李颀的边塞诗《古从军行》开头两句说:“白日登山望烽火,黄昏饮马傍交河”. 诗中隐含着一个有趣的数学问题——“将军饮马”,即将军在白天观望烽火台,黄昏时从山脚下某处出发,先到河边饮马,再回军营,怎样走才能使总路程最短?在平面直角坐标系中,设将军的出发点是$A(2,4)$,军营所在位置为$B(6,2)$,河岸线所在直线的方程为$x + y - 3 = 0$,若将军从出发点到河边饮马,再回到军营的总路程最短,则( )
A. 将军从出发点到河边的路线所在直线的方程是$6x - y - 8 = 0$
B. 将军在河边饮马的地点的坐标为$(\frac{13}{8},\frac{11}{8})$
C. 将军从河边回军营的路线所在直线的方程是$x - 6y + 6 = 0$
D. “将军饮马”走过的总路程为$5\sqrt{2}$
A. 将军从出发点到河边的路线所在直线的方程是$6x - y - 8 = 0$
B. 将军在河边饮马的地点的坐标为$(\frac{13}{8},\frac{11}{8})$
C. 将军从河边回军营的路线所在直线的方程是$x - 6y + 6 = 0$
D. “将军饮马”走过的总路程为$5\sqrt{2}$
答案:
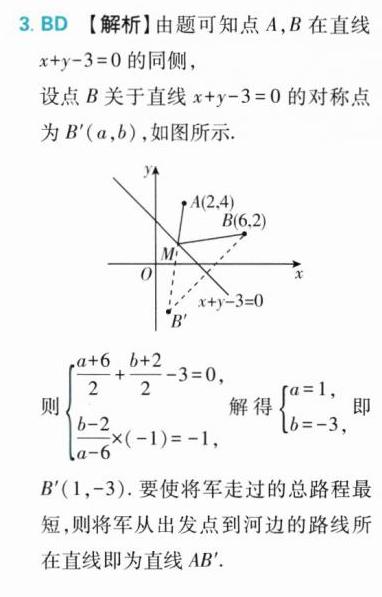
因为A(2,4),所以直线AB'的方程为$y + 3=\frac{4 + 3}{2 - 1}(x - 1)$,即7x - y - 10 = 0,故A错误.
设将军在河边饮马的地点为M,则M即为直线7x - y - 10 = 0与x + y - 3 = 0的交点,联立两直线方程解得$M(\frac{13}{8},\frac{11}{8})$,故B正确.
将军从河边回军营的路线所在直线为直线BM,又B(6,2),所以直线BM的方程为$y - 2=\frac{\frac{11}{8}-2}{\frac{13}{8}-6}(x - 6)$,即x - 7y + 8 = 0,故C错误.
总路程|MA|+|MB| = |MA|+|MB'| = |AB'| = $\sqrt{(2 - 1)^2+(4 + 3)^2}=5\sqrt{2}$,所以“将军饮马”走过的总路程为$5\sqrt{2}$,故D正确. 故选BD.

因为A(2,4),所以直线AB'的方程为$y + 3=\frac{4 + 3}{2 - 1}(x - 1)$,即7x - y - 10 = 0,故A错误.
设将军在河边饮马的地点为M,则M即为直线7x - y - 10 = 0与x + y - 3 = 0的交点,联立两直线方程解得$M(\frac{13}{8},\frac{11}{8})$,故B正确.
将军从河边回军营的路线所在直线为直线BM,又B(6,2),所以直线BM的方程为$y - 2=\frac{\frac{11}{8}-2}{\frac{13}{8}-6}(x - 6)$,即x - 7y + 8 = 0,故C错误.
总路程|MA|+|MB| = |MA|+|MB'| = |AB'| = $\sqrt{(2 - 1)^2+(4 + 3)^2}=5\sqrt{2}$,所以“将军饮马”走过的总路程为$5\sqrt{2}$,故D正确. 故选BD.
4. [河南南阳六校2023高二联考]著名数学家华罗庚曾说过:“数形结合百般好,隔离分家万事休”. 事实上,有很多代数问题可以转化为几何问题加以解决,如:求$\sqrt{(x - a)^2 + (y - b)^2}$可以转化为求平面上点$M(x,y)$与点$N(a,b)$之间的距离. 结合上述观点,可得$f(x)=\sqrt{x^2 + 8x + 20}+\sqrt{x^2 + 4x + 20}$的最小值为( )
A. $\sqrt{29}$
B. $\sqrt{31}$
C. $2\sqrt{10}$
D. $2+\sqrt{13}$
A. $\sqrt{29}$
B. $\sqrt{31}$
C. $2\sqrt{10}$
D. $2+\sqrt{13}$
答案:
4. C 【解析】$f(x)=\sqrt{x^2 + 8x + 20}+\sqrt{x^2 + 4x + 20}=\sqrt{(x + 4)^2+(0 - 2)^2}+\sqrt{(x + 2)^2+(0 + 4)^2}$,可以看作平面上点M(x,0)与点A(-4,2),B(-2,-4)的距离和,如图所示,连接AB,所以$f(x)=|MA|+|MB|\geqslant|AB|=\sqrt{(-4 + 2)^2+(2 + 4)^2}=2\sqrt{10}$,当且仅当A,M,B三点共线时等号成立. 故选C.
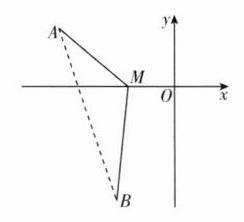
4. C 【解析】$f(x)=\sqrt{x^2 + 8x + 20}+\sqrt{x^2 + 4x + 20}=\sqrt{(x + 4)^2+(0 - 2)^2}+\sqrt{(x + 2)^2+(0 + 4)^2}$,可以看作平面上点M(x,0)与点A(-4,2),B(-2,-4)的距离和,如图所示,连接AB,所以$f(x)=|MA|+|MB|\geqslant|AB|=\sqrt{(-4 + 2)^2+(2 + 4)^2}=2\sqrt{10}$,当且仅当A,M,B三点共线时等号成立. 故选C.

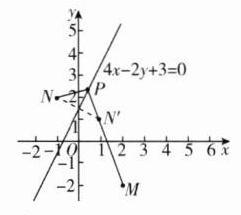
5. 已知实数$a$,$b$满足$4a - 2b + 3 = 0$,则$\sqrt{(a - 2)^2 + (b + 2)^2}-\sqrt{(a + 1)^2 + (b - 2)^2}$的最大值为________.
答案:
5. $\sqrt{10}$
【思路导引】
找到两个定点,M(2,-2),N(-1,2)
原式的几何意义为直线4x - 2y + 3 = 0上一点P到定点M,N的距离之差
点N关于直线4x - 2y + 3 = 0对称的点N'
P,M,N'三点共线时,所求距离之差最大
【解析】由题可知,$\sqrt{(a - 2)^2+(b + 2)^2}-\sqrt{(a + 1)^2+(b - 2)^2}$表示的是直线4x - 2y + 3 = 0上一点P(a,b)到定点M(2,-2),N(-1,2)的距离之差.
设点N关于直线4x - 2y + 3 = 0对称的点为N'(x_0,y_0),
则$\begin{cases}\frac{y_0 - 2}{x_0 + 1}=-\frac{1}{2}\\4\times\frac{x_0 - 1}{2}-2\times\frac{y_0 + 2}{2}+3 = 0\end{cases}$,
解得$\begin{cases}x_0 = 1\\y_0 = 1\end{cases}$,当N',P,M三点共线时,|PM|-|PN'|最大,即|PM|-|PN|最大,所以$\sqrt{(a - 2)^2+(b + 2)^2}-\sqrt{(a + 1)^2+(b - 2)^2}$的最大值为$\sqrt{(2 - 1)^2+(-2 - 1)^2}=\sqrt{10}$.
5. $\sqrt{10}$
【思路导引】
找到两个定点,M(2,-2),N(-1,2)
原式的几何意义为直线4x - 2y + 3 = 0上一点P到定点M,N的距离之差
点N关于直线4x - 2y + 3 = 0对称的点N'
P,M,N'三点共线时,所求距离之差最大
【解析】由题可知,$\sqrt{(a - 2)^2+(b + 2)^2}-\sqrt{(a + 1)^2+(b - 2)^2}$表示的是直线4x - 2y + 3 = 0上一点P(a,b)到定点M(2,-2),N(-1,2)的距离之差.
设点N关于直线4x - 2y + 3 = 0对称的点为N'(x_0,y_0),
则$\begin{cases}\frac{y_0 - 2}{x_0 + 1}=-\frac{1}{2}\\4\times\frac{x_0 - 1}{2}-2\times\frac{y_0 + 2}{2}+3 = 0\end{cases}$,
解得$\begin{cases}x_0 = 1\\y_0 = 1\end{cases}$,当N',P,M三点共线时,|PM|-|PN'|最大,即|PM|-|PN|最大,所以$\sqrt{(a - 2)^2+(b + 2)^2}-\sqrt{(a + 1)^2+(b - 2)^2}$的最大值为$\sqrt{(2 - 1)^2+(-2 - 1)^2}=\sqrt{10}$.

6. [安徽六安2024高二期中]过定点$A$的直线$(a + 1)x - y + 2 = 0$与过定点$B$的直线$x + (a + 1)y - 4a - 2 = 0$交于点$P(P$与$A$,$B$不重合),则$\triangle PAB$面积的最大值为( )
A. $\sqrt{2}$
B. $2\sqrt{2}$
C. 2
D. 4
A. $\sqrt{2}$
B. $2\sqrt{2}$
C. 2
D. 4
答案:
6. C 【解析】动直线(a + 1)x - y + 2 = 0化为y = (a + 1)x + 2,可得定点A(0,2),动直线x + (a + 1)y - 4a - 2 = 0化为(a + 1)(y - 4)+x + 2 = 0,可得定点B(-2,4).
因为(a + 1)×1 - 1×(a + 1)=0,所以直线(a + 1)x - y + 2 = 0与直线x + (a + 1)y - 4a - 2 = 0垂直,P为交点,所以PA⊥PB,所以|PA|²+|PB|² = |AB|²=(0 + 2)²+(2 - 4)² = 8. 则$S_{\triangle PAB}=\frac{1}{2}|PA|\cdot|PB|\leqslant\frac{1}{2}\cdot\frac{|PA|^2+|PB|^2}{2}=2$,当且仅当|PA| = |PB| = 2时,等号成立. 故△PAB面积的最大值为2. 故选C.
因为(a + 1)×1 - 1×(a + 1)=0,所以直线(a + 1)x - y + 2 = 0与直线x + (a + 1)y - 4a - 2 = 0垂直,P为交点,所以PA⊥PB,所以|PA|²+|PB|² = |AB|²=(0 + 2)²+(2 - 4)² = 8. 则$S_{\triangle PAB}=\frac{1}{2}|PA|\cdot|PB|\leqslant\frac{1}{2}\cdot\frac{|PA|^2+|PB|^2}{2}=2$,当且仅当|PA| = |PB| = 2时,等号成立. 故△PAB面积的最大值为2. 故选C.
7. 在平面直角坐标系$xOy$($O$为坐标原点)中,不过原点的两直线$l_1:x - my + 2m - 1 = 0$,$l_2:mx + y - m - 2 = 0$的交点为$P$,过点$O$分别向直线$l_1$,$l_2$引垂线,垂足分别为$M$,$N$,则四边形$OMPN$面积的最大值为( )
A. 3
B. $\frac{3}{2}$
C. 5
D. $\frac{5}{2}$
A. 3
B. $\frac{3}{2}$
C. 5
D. $\frac{5}{2}$
答案:
7. D 【解析】将直线l₁的方程变形得x - 1 + m(2 - y)=0,由$\begin{cases}x - 1 = 0\\2 - y = 0\end{cases}$,得$\begin{cases}x = 1\\y = 2\end{cases}$,则直线l₁过定点(1,2),同理可知,直线l₂过定点(1,2),所以直线l₁和直线l₂的交点P的坐标为(1,2),由1×m+( - m)×1 = 0可知直线l₁⊥l₂,连接OP.
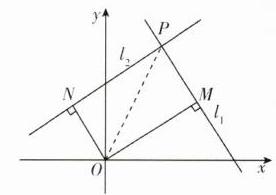
所以四边形OMPN为矩形,且|OP| = $\sqrt{1^2+2^2}=\sqrt{5}$.
设|OM| = a,|ON| = b,则a² + b² = 5,四边形OMPN的面积S = |OM|·|ON| = ab≤$\frac{a^2 + b^2}{2}=\frac{5}{2}$,
当且仅当$\begin{cases}a = b\\a^2 + b^2 = 5\end{cases}$,即$a = b=\frac{\sqrt{10}}{2}$时,等号成立,因此,四边形OMPN面积的最大值为$\frac{5}{2}$,故选D.
7. D 【解析】将直线l₁的方程变形得x - 1 + m(2 - y)=0,由$\begin{cases}x - 1 = 0\\2 - y = 0\end{cases}$,得$\begin{cases}x = 1\\y = 2\end{cases}$,则直线l₁过定点(1,2),同理可知,直线l₂过定点(1,2),所以直线l₁和直线l₂的交点P的坐标为(1,2),由1×m+( - m)×1 = 0可知直线l₁⊥l₂,连接OP.

所以四边形OMPN为矩形,且|OP| = $\sqrt{1^2+2^2}=\sqrt{5}$.
设|OM| = a,|ON| = b,则a² + b² = 5,四边形OMPN的面积S = |OM|·|ON| = ab≤$\frac{a^2 + b^2}{2}=\frac{5}{2}$,
当且仅当$\begin{cases}a = b\\a^2 + b^2 = 5\end{cases}$,即$a = b=\frac{\sqrt{10}}{2}$时,等号成立,因此,四边形OMPN面积的最大值为$\frac{5}{2}$,故选D.
8. [山东烟台2024高二月考]已知定点$P(6,4)$与定直线$l_1:y = 4x$,过点$P$的直线$l$与$l_1$交于第一象限点$Q$,与$x$轴正半轴交于点$M$,则使$\triangle OQM$面积最小的直线$l$的方程为________.
答案:
8. x + y - 10 = 0
【思路导引】根据题意,画出平面直角坐标系及点的位置,根据直线l过点P设出直线l的方程,分别求出点Q,M的坐标,从而用代数式表示出△OQM的面积,进而可求出最小值. 注意分直线斜率存在和不存在两种情况讨论.
【解析】当直线l的斜率不存在时,直线l的方程为x = 6,由$\begin{cases}x = 6\\y = 4x\end{cases}$,得$\begin{cases}x = 6\\y = 24\end{cases}$,即Q(6,24),又易知M(6,0),所以△OQM的面积$S=\frac{1}{2}\times6\times24 = 72$.
当直线l的斜率存在时,不妨设直线l的方程为y - 4 = k(x - 6),令y = 0,得$x = 6-\frac{4}{k}$,又由$\begin{cases}y = 4x\\y - 4 = k(x - 6)\end{cases}$,消x得到$y=\frac{24k - 16}{k - 4}$.
由题知$\begin{cases}6-\frac{4}{k}>0\\\frac{24k - 16}{k - 4}>0\end{cases}$,得k<0或k>4.


8. x + y - 10 = 0
【思路导引】根据题意,画出平面直角坐标系及点的位置,根据直线l过点P设出直线l的方程,分别求出点Q,M的坐标,从而用代数式表示出△OQM的面积,进而可求出最小值. 注意分直线斜率存在和不存在两种情况讨论.
【解析】当直线l的斜率不存在时,直线l的方程为x = 6,由$\begin{cases}x = 6\\y = 4x\end{cases}$,得$\begin{cases}x = 6\\y = 24\end{cases}$,即Q(6,24),又易知M(6,0),所以△OQM的面积$S=\frac{1}{2}\times6\times24 = 72$.
当直线l的斜率存在时,不妨设直线l的方程为y - 4 = k(x - 6),令y = 0,得$x = 6-\frac{4}{k}$,又由$\begin{cases}y = 4x\\y - 4 = k(x - 6)\end{cases}$,消x得到$y=\frac{24k - 16}{k - 4}$.
由题知$\begin{cases}6-\frac{4}{k}>0\\\frac{24k - 16}{k - 4}>0\end{cases}$,得k<0或k>4.


查看更多完整答案,请扫码查看


