2024年高中必刷题高二数学选择性必修第一册人教B版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2024年高中必刷题高二数学选择性必修第一册人教B版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第62页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
1. [山东滨州实验中学2024高二期末]与曲线$\frac{x^{2}}{16}+\frac{y^{2}}{36}=1$共焦点,且与双曲线$\frac{x^{2}}{4}-\frac{y^{2}}{6}=1$共渐近线的双曲线的方程为 ( )
A. $\frac{y^{2}}{12}-\frac{x^{2}}{8}=1$
B. $\frac{y^{2}}{8}-\frac{x^{2}}{12}=1$
C. $\frac{x^{2}}{12}-\frac{y^{2}}{8}=1$
D. $\frac{x^{2}}{8}-\frac{y^{2}}{12}=1$
A. $\frac{y^{2}}{12}-\frac{x^{2}}{8}=1$
B. $\frac{y^{2}}{8}-\frac{x^{2}}{12}=1$
C. $\frac{x^{2}}{12}-\frac{y^{2}}{8}=1$
D. $\frac{x^{2}}{8}-\frac{y^{2}}{12}=1$
答案:
A 【解析】曲线$\frac{x^{2}}{16}+\frac{y^{2}}{36}=1$为椭圆,焦点在$y$轴上,且$c^{2}=36 - 16 = 20$。
因为所求双曲线与双曲线$\frac{x^{2}}{4}-\frac{y^{2}}{6}=1$共渐近线,所以设所求双曲线为$\frac{x^{2}}{4}-\frac{y^{2}}{6}=\lambda(\lambda\lt0)$,即$\frac{y^{2}}{-6\lambda}-\frac{x^{2}}{-4\lambda}=1$,则$c^{2}=-6\lambda - 4\lambda = 20$,解得$\lambda = - 2$,所以所求双曲线方程为$\frac{y^{2}}{12}-\frac{x^{2}}{8}=1$。故选A。
【二级结论】与双曲线$mx^{2}-ny^{2}=1(mn\gt0)$共渐近线的双曲线方程为$mx^{2}-ny^{2}=\lambda(\lambda\neq0)$。
因为所求双曲线与双曲线$\frac{x^{2}}{4}-\frac{y^{2}}{6}=1$共渐近线,所以设所求双曲线为$\frac{x^{2}}{4}-\frac{y^{2}}{6}=\lambda(\lambda\lt0)$,即$\frac{y^{2}}{-6\lambda}-\frac{x^{2}}{-4\lambda}=1$,则$c^{2}=-6\lambda - 4\lambda = 20$,解得$\lambda = - 2$,所以所求双曲线方程为$\frac{y^{2}}{12}-\frac{x^{2}}{8}=1$。故选A。
【二级结论】与双曲线$mx^{2}-ny^{2}=1(mn\gt0)$共渐近线的双曲线方程为$mx^{2}-ny^{2}=\lambda(\lambda\neq0)$。
2. [黑龙江哈尔滨第九中学2023高二月考]为了增强某会议主席台的亮度,且为了避免主席台就座人员面对强光的不适,灯光设计人员巧妙地通过双曲线镜面反射出发散光线达到了预期的效果.如图,从双曲线右焦点$F_{2}$发出的光线的反射光线的反向延长线经过左焦点$F_{1}$.已知双曲线的离心率为$\sqrt{2}$,则当$|F_{1}P|$与$|F_{1}F_{2}|$恰好相等时,$\cos\angle F_{1}F_{2}P=$ ( )
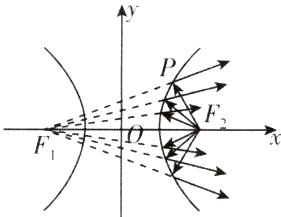
A. $\frac{2 - \sqrt{2}}{4}$
B. $\frac{\sqrt{2}}{2}$
C. $\frac{1}{2}$
D. $\frac{\sqrt{2}-1}{2}$

A. $\frac{2 - \sqrt{2}}{4}$
B. $\frac{\sqrt{2}}{2}$
C. $\frac{1}{2}$
D. $\frac{\sqrt{2}-1}{2}$
答案:
A 【解析】$\because$离心率$e = \frac{c}{a}=\sqrt{2}$,$\therefore c = \sqrt{2}a$。
又$|F_{1}P| = |F_{1}F_{2}| = 2c = 2\sqrt{2}a$,则根据双曲线的定义可知,$|F_{2}P| = |F_{1}P| - 2a=(2\sqrt{2}-2)a$,
$\therefore\cos\angle F_{1}F_{2}P=\frac{|PF_{2}|^{2}+|F_{1}F_{2}|^{2}-|PF_{1}|^{2}}{2|PF_{2}|\cdot|F_{1}F_{2}|}$
$=\frac{(2\sqrt{2}-2)^{2}a^{2}+8a^{2}-8a^{2}}{2(2\sqrt{2}-2)a\cdot2\sqrt{2}a}$
$=\frac{\sqrt{2}-1}{2\sqrt{2}}=\frac{2-\sqrt{2}}{4}$。
故选A。
又$|F_{1}P| = |F_{1}F_{2}| = 2c = 2\sqrt{2}a$,则根据双曲线的定义可知,$|F_{2}P| = |F_{1}P| - 2a=(2\sqrt{2}-2)a$,
$\therefore\cos\angle F_{1}F_{2}P=\frac{|PF_{2}|^{2}+|F_{1}F_{2}|^{2}-|PF_{1}|^{2}}{2|PF_{2}|\cdot|F_{1}F_{2}|}$
$=\frac{(2\sqrt{2}-2)^{2}a^{2}+8a^{2}-8a^{2}}{2(2\sqrt{2}-2)a\cdot2\sqrt{2}a}$
$=\frac{\sqrt{2}-1}{2\sqrt{2}}=\frac{2-\sqrt{2}}{4}$。
故选A。
3. [重庆八中2024高二期中]如图所示,双曲线型冷却塔的外形是离心率为3的双曲线的一部分绕其虚轴旋转所成的曲面,已知该冷却塔的上口半径为3 m,下口半径为4 m,高为8 m(数据以外壁即冷却塔外侧表面计算),则冷却塔的最小直径为 ( )

A. $\frac{\sqrt{574}}{8}$ m
B. $\frac{\sqrt{287}}{8}$ m
C. $\frac{\sqrt{574}}{4}$ m
D. $\frac{\sqrt{287}}{4}$ m

A. $\frac{\sqrt{574}}{8}$ m
B. $\frac{\sqrt{287}}{8}$ m
C. $\frac{\sqrt{574}}{4}$ m
D. $\frac{\sqrt{287}}{4}$ m
答案:
C 【解析】根据题意,作出冷却塔对应的双曲线,并建立相应的平面直角坐标系,如图所示,设双曲线方程为$\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1(a\gt0,b\gt0)$,

因为冷却塔的上口半径为$3m$,下口半径为$4m$,高为$8m$,
所以设双曲线上的点$A(3,y_{1})$,$B(4,y_{2})$,且$y_{1}-y_{2}=8$,
将$A$,$B$的坐标代入双曲线方程可得$\begin{cases}\frac{9}{a^{2}}-\frac{y_{1}^{2}}{b^{2}}=1\\\frac{16}{a^{2}}-\frac{y_{2}^{2}}{b^{2}}=1\end{cases}$,两式相减得$\frac{7}{a^{2}}=\frac{y_{2}^{2}-y_{1}^{2}}{b^{2}}=\frac{(y_{2}-y_{1})(y_{2}+y_{1})}{b^{2}}$①。
因为双曲线的离心率为$3$,所以$\frac{b^{2}}{a^{2}}=\frac{c^{2}-a^{2}}{a^{2}}=e^{2}-1 = 8$,所以$b^{2}=8a^{2}$,
代入①式可得$\frac{7}{a^{2}}=\frac{-8(y_{2}+y_{1})}{8a^{2}}$,得$y_{2}+y_{1}=-7$,所以$y_{1}=\frac{1}{2}$,
将点$(3,\frac{1}{2})$的坐标代入双曲线方程可得$\frac{9}{a^{2}}-\frac{1}{32a^{2}}=1$,解得$a=\frac{\sqrt{574}}{8}$。
所以冷却塔的最小直径为$2a=\frac{\sqrt{574}}{4}$,故选C。
C 【解析】根据题意,作出冷却塔对应的双曲线,并建立相应的平面直角坐标系,如图所示,设双曲线方程为$\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1(a\gt0,b\gt0)$,

因为冷却塔的上口半径为$3m$,下口半径为$4m$,高为$8m$,
所以设双曲线上的点$A(3,y_{1})$,$B(4,y_{2})$,且$y_{1}-y_{2}=8$,
将$A$,$B$的坐标代入双曲线方程可得$\begin{cases}\frac{9}{a^{2}}-\frac{y_{1}^{2}}{b^{2}}=1\\\frac{16}{a^{2}}-\frac{y_{2}^{2}}{b^{2}}=1\end{cases}$,两式相减得$\frac{7}{a^{2}}=\frac{y_{2}^{2}-y_{1}^{2}}{b^{2}}=\frac{(y_{2}-y_{1})(y_{2}+y_{1})}{b^{2}}$①。
因为双曲线的离心率为$3$,所以$\frac{b^{2}}{a^{2}}=\frac{c^{2}-a^{2}}{a^{2}}=e^{2}-1 = 8$,所以$b^{2}=8a^{2}$,
代入①式可得$\frac{7}{a^{2}}=\frac{-8(y_{2}+y_{1})}{8a^{2}}$,得$y_{2}+y_{1}=-7$,所以$y_{1}=\frac{1}{2}$,
将点$(3,\frac{1}{2})$的坐标代入双曲线方程可得$\frac{9}{a^{2}}-\frac{1}{32a^{2}}=1$,解得$a=\frac{\sqrt{574}}{8}$。
所以冷却塔的最小直径为$2a=\frac{\sqrt{574}}{4}$,故选C。
4. [重庆育才中学2024高二期中]已知$F_{1}(-c,0),F_{2}(c,0)$为双曲线$\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1(a > 0,b > 0)$的两个焦点,$P$为双曲线上一点,且$\overrightarrow{PF_{1}}\cdot\overrightarrow{PF_{2}}=-\frac{1}{2}c^{2}$,则此双曲线离心率的取值范围为 ( )
A. $(1,\sqrt{2}]$
B. $(1,2]$
C. $[\sqrt{2},+\infty)$
D. $(2,+\infty)$
A. $(1,\sqrt{2}]$
B. $(1,2]$
C. $[\sqrt{2},+\infty)$
D. $(2,+\infty)$
答案:
C 【解析】设$|\overrightarrow{PF_{1}}| = m$,$|\overrightarrow{PF_{2}}| = n$,$\angle F_{1}PF_{2}=\theta$,由$\overrightarrow{PF_{1}}\cdot\overrightarrow{PF_{2}}=-\frac{1}{2}c^{2}$,可得$mn\cos\theta=-\frac{1}{2}c^{2}\lt0$,
显然$\theta\in(\frac{\pi}{2},\pi]$,整理可得$mn = -\frac{c^{2}}{2\cos\theta}$。
由$|\overrightarrow{PF_{1}}-\overrightarrow{PF_{2}}| = |\overrightarrow{F_{2}F_{1}}| = 2c$,
得$(\overrightarrow{PF_{1}}-\overrightarrow{PF_{2}})^{2}=|\overrightarrow{PF_{1}}|^{2}-2\overrightarrow{PF_{1}}\cdot\overrightarrow{PF_{2}}+|\overrightarrow{PF_{2}}|^{2}=m^{2}-2\cdot(-\frac{1}{2}c^{2})+n^{2}=4c^{2}$,
解得$m^{2}+n^{2}=3c^{2}$。由双曲线的定义可知$|m - n| = 2a$,
则有$(m - n)^{2}=m^{2}-2mn + n^{2}=4a^{2}$,整理可得$4a^{2}=3c^{2}+\frac{c^{2}}{\cos\theta}$,
化简可得$\frac{c^{2}}{a^{2}}=\frac{4\cos\theta}{3\cos\theta + 1}=\frac{4}{3}-\frac{4}{9\cos\theta + 3}$,因为$\frac{\pi}{2}\lt\theta\leqslant\pi$,且$\frac{c^{2}}{a^{2}}\gt1$,
所以$-1\leqslant\cos\theta\lt0\Rightarrow - 6\leqslant9\cos\theta + 3\lt3$,
可得$\frac{4}{9\cos\theta + 3}\leqslant-\frac{2}{3}$或$\frac{4}{9\cos\theta + 3}\gt\frac{4}{3}$,
所以$\frac{4}{3}-\frac{4}{9\cos\theta + 3}\geqslant2$或$\frac{4}{3}-\frac{4}{9\cos\theta + 3}\lt0$,所以$\frac{c^{2}}{a^{2}}\geqslant2$,
解得$e\geqslant\sqrt{2}$。故选C。
显然$\theta\in(\frac{\pi}{2},\pi]$,整理可得$mn = -\frac{c^{2}}{2\cos\theta}$。
由$|\overrightarrow{PF_{1}}-\overrightarrow{PF_{2}}| = |\overrightarrow{F_{2}F_{1}}| = 2c$,
得$(\overrightarrow{PF_{1}}-\overrightarrow{PF_{2}})^{2}=|\overrightarrow{PF_{1}}|^{2}-2\overrightarrow{PF_{1}}\cdot\overrightarrow{PF_{2}}+|\overrightarrow{PF_{2}}|^{2}=m^{2}-2\cdot(-\frac{1}{2}c^{2})+n^{2}=4c^{2}$,
解得$m^{2}+n^{2}=3c^{2}$。由双曲线的定义可知$|m - n| = 2a$,
则有$(m - n)^{2}=m^{2}-2mn + n^{2}=4a^{2}$,整理可得$4a^{2}=3c^{2}+\frac{c^{2}}{\cos\theta}$,
化简可得$\frac{c^{2}}{a^{2}}=\frac{4\cos\theta}{3\cos\theta + 1}=\frac{4}{3}-\frac{4}{9\cos\theta + 3}$,因为$\frac{\pi}{2}\lt\theta\leqslant\pi$,且$\frac{c^{2}}{a^{2}}\gt1$,
所以$-1\leqslant\cos\theta\lt0\Rightarrow - 6\leqslant9\cos\theta + 3\lt3$,
可得$\frac{4}{9\cos\theta + 3}\leqslant-\frac{2}{3}$或$\frac{4}{9\cos\theta + 3}\gt\frac{4}{3}$,
所以$\frac{4}{3}-\frac{4}{9\cos\theta + 3}\geqslant2$或$\frac{4}{3}-\frac{4}{9\cos\theta + 3}\lt0$,所以$\frac{c^{2}}{a^{2}}\geqslant2$,
解得$e\geqslant\sqrt{2}$。故选C。
5. (多选)已知$F_{1},F_{2}$是椭圆$\frac{x^{2}}{a_{1}^{2}}+\frac{y^{2}}{b_{1}^{2}}=1(a_{1}>b_{1}>0)$和双曲线$\frac{x^{2}}{a_{2}^{2}}-\frac{y^{2}}{b_{2}^{2}}=1(a_{2}>0,b_{2}>0)$的公共焦点,$P$是它们的一个公共点,且$\angle F_{1}PF_{2}=\frac{\pi}{3}$,则以下结论正确的是 ( )
A. $a_{1}^{2}-b_{1}^{2}=a_{2}^{2}-b_{2}^{2}$
B. $b_{1}^{2}=3b_{2}^{2}$
C. $\frac{1}{4e_{1}^{2}}+\frac{1}{4e_{2}^{2}}=1$
D. $e_{1}^{2}+e_{2}^{2}$的最小值为$1+\frac{\sqrt{3}}{2}$
A. $a_{1}^{2}-b_{1}^{2}=a_{2}^{2}-b_{2}^{2}$
B. $b_{1}^{2}=3b_{2}^{2}$
C. $\frac{1}{4e_{1}^{2}}+\frac{1}{4e_{2}^{2}}=1$
D. $e_{1}^{2}+e_{2}^{2}$的最小值为$1+\frac{\sqrt{3}}{2}$
答案:
BD 【解析】由题意可得$a_{1}^{2}-b_{1}^{2}=a_{2}^{2}+b_{2}^{2}$,故A错误。
可设$P$是第一象限的点,$|\ PF_{1}| = m$,$|\ PF_{2}| = n$,由椭圆及双曲线的定义可得$m + n = 2a_{1}$,$m - n = 2a_{2}$,解得$m = a_{1}+a_{2}$,$n = a_{1}-a_{2}$。
因为$\angle F_{1}PF_{2}=\frac{\pi}{3}$,在$\triangle F_{1}PF_{2}$中,
由余弦定理可得
$\cos\angle F_{1}PF_{2}=\frac{|PF_{1}|^{2}+|PF_{2}|^{2}-|F_{1}F_{2}|^{2}}{2|PF_{1}|\cdot|PF_{2}|}=\frac{m^{2}+n^{2}-4c^{2}}{2mn}=\frac{1}{2}$,
整理可得$a_{1}^{2}+3a_{2}^{2}=4c^{2}$。
又$a_{1}^{2}-b_{1}^{2}=a_{2}^{2}+b_{2}^{2}=c^{2}$,则$b_{1}^{2}-3b_{2}^{2}=a_{1}^{2}-c^{2}-(3c^{2}-3a_{2}^{2}) = 0$,故B正确。
由$a_{1}^{2}+3a_{2}^{2}=4c^{2}$,可得$\frac{a_{1}^{2}}{c^{2}}+\frac{3a_{2}^{2}}{c^{2}} = 4$,即$\frac{1}{e_{1}^{2}}+\frac{3}{e_{2}^{2}} = 4$,故C错误。
$e_{1}^{2}+e_{2}^{2}=\frac{1}{4}(\frac{1}{e_{1}^{2}}+\frac{3}{e_{2}^{2}})(e_{1}^{2}+e_{2}^{2})=\frac{1}{4}(1 + 3+\frac{e_{2}^{2}}{e_{1}^{2}}+\frac{3e_{1}^{2}}{e_{2}^{2}})\geqslant\frac{1}{4}(4 + 2\sqrt{3})$,
当且仅当$e_{2}^{2}=\sqrt{3}e_{1}^{2}$时,取得等号,即有$e_{1}^{2}+e_{2}^{2}$的最小值为$1+\frac{\sqrt{3}}{2}$,故D正确。
故选BD。
可设$P$是第一象限的点,$|\ PF_{1}| = m$,$|\ PF_{2}| = n$,由椭圆及双曲线的定义可得$m + n = 2a_{1}$,$m - n = 2a_{2}$,解得$m = a_{1}+a_{2}$,$n = a_{1}-a_{2}$。
因为$\angle F_{1}PF_{2}=\frac{\pi}{3}$,在$\triangle F_{1}PF_{2}$中,
由余弦定理可得
$\cos\angle F_{1}PF_{2}=\frac{|PF_{1}|^{2}+|PF_{2}|^{2}-|F_{1}F_{2}|^{2}}{2|PF_{1}|\cdot|PF_{2}|}=\frac{m^{2}+n^{2}-4c^{2}}{2mn}=\frac{1}{2}$,
整理可得$a_{1}^{2}+3a_{2}^{2}=4c^{2}$。
又$a_{1}^{2}-b_{1}^{2}=a_{2}^{2}+b_{2}^{2}=c^{2}$,则$b_{1}^{2}-3b_{2}^{2}=a_{1}^{2}-c^{2}-(3c^{2}-3a_{2}^{2}) = 0$,故B正确。
由$a_{1}^{2}+3a_{2}^{2}=4c^{2}$,可得$\frac{a_{1}^{2}}{c^{2}}+\frac{3a_{2}^{2}}{c^{2}} = 4$,即$\frac{1}{e_{1}^{2}}+\frac{3}{e_{2}^{2}} = 4$,故C错误。
$e_{1}^{2}+e_{2}^{2}=\frac{1}{4}(\frac{1}{e_{1}^{2}}+\frac{3}{e_{2}^{2}})(e_{1}^{2}+e_{2}^{2})=\frac{1}{4}(1 + 3+\frac{e_{2}^{2}}{e_{1}^{2}}+\frac{3e_{1}^{2}}{e_{2}^{2}})\geqslant\frac{1}{4}(4 + 2\sqrt{3})$,
当且仅当$e_{2}^{2}=\sqrt{3}e_{1}^{2}$时,取得等号,即有$e_{1}^{2}+e_{2}^{2}$的最小值为$1+\frac{\sqrt{3}}{2}$,故D正确。
故选BD。
6. 已知$F$是双曲线$C:x^{2}-\frac{y^{2}}{8}=1$的右焦点,$P$是双曲线$C$左支上的一点,且点$A$的坐标为$(0,6\sqrt{6})$,则$\triangle APF$的周长的最小值为 .
答案:
32 【解析】如图,设双曲线的左焦点为$F_{1}$,连接$PF_{1}$。
由双曲线方程$x^{2}-\frac{y^{2}}{8}=1$可知$a = 1$,$c = 3$,故$F(3,0)$,$F_{1}(-3,0)$。
当点$P$在双曲线左支上运动时,由双曲线定义可知$|PF|-|PF_{1}| = 2$,所以$|PF| = |PF_{1}| + 2$,从而$\triangle APF$的周长为$|AP|+|PF|+|AF| = |AP|+|PF_{1}|+2+|AF|$。
因为$|AF|=\sqrt{3^{2}+(6\sqrt{6})^{2}} = 15$为定值,所以当$|AP|+|PF_{1}|$最小时,$\triangle APF$的周长最小。
由图可知,当$|AP|+|PF_{1}|$最小时,点$P$为线段$AF_{1}$与双曲线的交点,且$|AP|+|PF_{1}| = |AF_{1}| = 15$,所以$\triangle APF$周长的最小值为$32$。

32 【解析】如图,设双曲线的左焦点为$F_{1}$,连接$PF_{1}$。
由双曲线方程$x^{2}-\frac{y^{2}}{8}=1$可知$a = 1$,$c = 3$,故$F(3,0)$,$F_{1}(-3,0)$。
当点$P$在双曲线左支上运动时,由双曲线定义可知$|PF|-|PF_{1}| = 2$,所以$|PF| = |PF_{1}| + 2$,从而$\triangle APF$的周长为$|AP|+|PF|+|AF| = |AP|+|PF_{1}|+2+|AF|$。
因为$|AF|=\sqrt{3^{2}+(6\sqrt{6})^{2}} = 15$为定值,所以当$|AP|+|PF_{1}|$最小时,$\triangle APF$的周长最小。
由图可知,当$|AP|+|PF_{1}|$最小时,点$P$为线段$AF_{1}$与双曲线的交点,且$|AP|+|PF_{1}| = |AF_{1}| = 15$,所以$\triangle APF$周长的最小值为$32$。

7. [2023全国高中数学联赛重庆预赛]双曲线$\frac{x^{2}}{a^{2}}-\frac{y^{2}}{16}=1$的左、右焦点分别为$A,B$,$P$是双曲线上一点.若$\triangle PAB$的内切圆圆心为$(3,1)$,则$\triangle PAB$外接圆的半径为 .
答案:
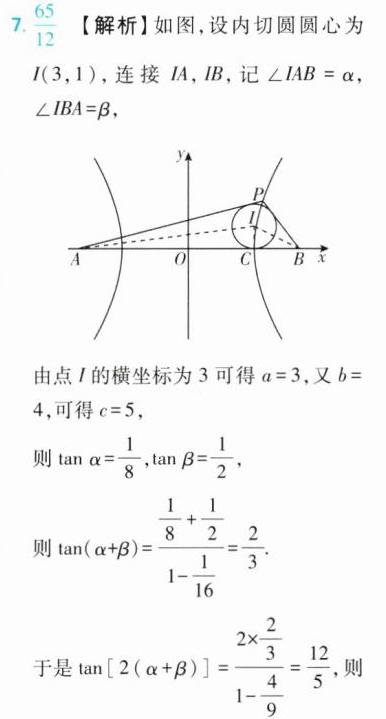



查看更多完整答案,请扫码查看


