2024年高中必刷题高二数学选择性必修第一册人教B版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2024年高中必刷题高二数学选择性必修第一册人教B版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第70页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
10. [吉林大学附中2024高二期中]已知双曲线$\frac{x^{2}}{5 - m}-\frac{y^{2}}{m - 1}=1(1\lt m\lt5)$的一个焦点与抛物线$C:y^{2}=2px(p\gt0)$的焦点重合.
(1)求抛物线$C$的方程;
(2)若直线$l:x = ty + 8$交抛物线$C$于$A,B$两点,$O$为原点,求证:以$AB$为直径的圆经过原点$O$.
(1)求抛物线$C$的方程;
(2)若直线$l:x = ty + 8$交抛物线$C$于$A,B$两点,$O$为原点,求证:以$AB$为直径的圆经过原点$O$.
答案:
(1)【解】由双曲线方程$\frac{x^{2}}{5 - m}-\frac{y^{2}}{m - 1}=1(1<m<5)$知其焦点在$x$轴上且焦点坐标为$F_{1}(-2,0)$,$F_{2}(2,0)$,所以$F_{2}(2,0)$为抛物线$C:y^{2}=2px(p>0)$的焦点,可得$\frac{p}{2}=2$,则$p = 4$,
所以抛物线$C$的方程为$y^{2}=8x$.
(2)【证明】设$A(x_{1},y_{1})$,$B(x_{2},y_{2})$,
联立$\begin{cases}x = ty + 8\\y^{2}=8x\end{cases}$,可得$y^{2}-8ty - 64 = 0$,
$\Delta=64t^{2}+4\times64>0$,
由一元二次方程根与系数的关系得$y_{1}+y_{2}=8t$,$y_{1}y_{2}=-64$,
所以$\overrightarrow{OA}\cdot\overrightarrow{OB}=x_{1}x_{2}+y_{1}y_{2}=(ty_{1}+8)(ty_{2}+8)+y_{1}y_{2}=(t^{2}+1)y_{1}y_{2}+8t(y_{1}+y_{2})+64=(t^{2}+1)(-64)+8t\cdot8t+64 = 0$. 所以$OA\perp OB$,所以以$AB$为直径的圆经过原点$O$. 得证.
(1)【解】由双曲线方程$\frac{x^{2}}{5 - m}-\frac{y^{2}}{m - 1}=1(1<m<5)$知其焦点在$x$轴上且焦点坐标为$F_{1}(-2,0)$,$F_{2}(2,0)$,所以$F_{2}(2,0)$为抛物线$C:y^{2}=2px(p>0)$的焦点,可得$\frac{p}{2}=2$,则$p = 4$,
所以抛物线$C$的方程为$y^{2}=8x$.
(2)【证明】设$A(x_{1},y_{1})$,$B(x_{2},y_{2})$,
联立$\begin{cases}x = ty + 8\\y^{2}=8x\end{cases}$,可得$y^{2}-8ty - 64 = 0$,
$\Delta=64t^{2}+4\times64>0$,
由一元二次方程根与系数的关系得$y_{1}+y_{2}=8t$,$y_{1}y_{2}=-64$,
所以$\overrightarrow{OA}\cdot\overrightarrow{OB}=x_{1}x_{2}+y_{1}y_{2}=(ty_{1}+8)(ty_{2}+8)+y_{1}y_{2}=(t^{2}+1)y_{1}y_{2}+8t(y_{1}+y_{2})+64=(t^{2}+1)(-64)+8t\cdot8t+64 = 0$. 所以$OA\perp OB$,所以以$AB$为直径的圆经过原点$O$. 得证.
12. [山东潍坊安丘第一中学2023高二月考]设椭圆中心在原点$O$上,焦点在$x$轴上,离心率为$\frac{\sqrt{2}}{2}$,椭圆上一点$P$到两焦点的距离的和等于$\sqrt{6}$.
(1)求椭圆的方程;
(2)若直线$x + y + m = 0$交椭圆于$A,B$两点,且$OA\perp OB$,求$m$的值;
(3)在(2)的结论下,求$AB$的长.
(1)求椭圆的方程;
(2)若直线$x + y + m = 0$交椭圆于$A,B$两点,且$OA\perp OB$,求$m$的值;
(3)在(2)的结论下,求$AB$的长.
答案:
【解】
(1) 因为椭圆焦点在$x$轴上,所以设椭圆的方程为$\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1(a>b>0)$,则$e=\frac{c}{a}=\frac{\sqrt{2}}{2}$. 又椭圆上一点到两焦点的距离和为$\sqrt{6}$,所以$2a=\sqrt{6}$,$a=\frac{\sqrt{6}}{2}$,所以$c=\frac{\sqrt{3}}{2}$,$b=\sqrt{a^{2}-c^{2}}=\sqrt{(\frac{\sqrt{6}}{2})^{2}-(\frac{\sqrt{3}}{2})^{2}}=\frac{\sqrt{3}}{2}$,所以椭圆的方程为$\frac{x^{2}}{\frac{3}{2}}+\frac{y^{2}}{\frac{3}{4}}=1$,即$\frac{2x^{2}}{3}+\frac{4y^{2}}{3}=1$.
(2) 由
(1)知,椭圆的方程为$\frac{2x^{2}}{3}+\frac{4y^{2}}{3}=1$,即$2x^{2}+4y^{2}=3$.
设$A(x_{1},y_{1})$,$B(x_{2},y_{2})$,联立$\begin{cases}2x^{2}+4y^{2}=3\\x + y + m = 0\end{cases}$,得$6y^{2}+4my+2m^{2}-3 = 0$,$\Delta=16m^{2}-24(2m^{2}-3)=72 - 32m^{2}>0$,$y_{1}y_{2}=\frac{2m^{2}-3}{6}$,$y_{1}+y_{2}=-\frac{2m}{3}$.
又$OA\perp OB$,所以$\overrightarrow{OA}\cdot\overrightarrow{OB}=y_{1}y_{2}+x_{1}x_{2}=0$,又$x=-y - m$,所以$y_{1}y_{2}+(-y_{1}-m)(-y_{2}-m)=0$,
整理得$2y_{1}y_{2}+(y_{1}+y_{2})m+m^{2}=0$,
即$2\times\frac{2m^{2}-3}{6}+(-\frac{2m}{3})m+m^{2}=0$,解得$m^{2}=1$,满足$72 - 32m^{2}>0$,
所以$m=\pm1$.
(3)$|AB|=\sqrt{(x_{1}-x_{2})^{2}+(y_{1}-y_{2})^{2}}=\sqrt{[(-y_{1}-m)-(-y_{2}-m)]^{2}+(y_{1}-y_{2})^{2}}=\sqrt{2(y_{1}-y_{2})^{2}}=\sqrt{2}\cdot\sqrt{(y_{1}+y_{2})^{2}-4y_{1}y_{2}}$.
当$m = 1$时,由
(2)得$y_{1}+y_{2}=-\frac{2}{3}$,$y_{1}y_{2}=-\frac{1}{6}$,所以$|AB|=\sqrt{2}\times\frac{\sqrt{10}}{3}=\frac{2\sqrt{5}}{3}$.
由对称性可知当$m=-1$时,也有$|AB|=\frac{2\sqrt{5}}{3}$. 所以$|AB|=\frac{2\sqrt{5}}{3}$.
(1) 因为椭圆焦点在$x$轴上,所以设椭圆的方程为$\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1(a>b>0)$,则$e=\frac{c}{a}=\frac{\sqrt{2}}{2}$. 又椭圆上一点到两焦点的距离和为$\sqrt{6}$,所以$2a=\sqrt{6}$,$a=\frac{\sqrt{6}}{2}$,所以$c=\frac{\sqrt{3}}{2}$,$b=\sqrt{a^{2}-c^{2}}=\sqrt{(\frac{\sqrt{6}}{2})^{2}-(\frac{\sqrt{3}}{2})^{2}}=\frac{\sqrt{3}}{2}$,所以椭圆的方程为$\frac{x^{2}}{\frac{3}{2}}+\frac{y^{2}}{\frac{3}{4}}=1$,即$\frac{2x^{2}}{3}+\frac{4y^{2}}{3}=1$.
(2) 由
(1)知,椭圆的方程为$\frac{2x^{2}}{3}+\frac{4y^{2}}{3}=1$,即$2x^{2}+4y^{2}=3$.
设$A(x_{1},y_{1})$,$B(x_{2},y_{2})$,联立$\begin{cases}2x^{2}+4y^{2}=3\\x + y + m = 0\end{cases}$,得$6y^{2}+4my+2m^{2}-3 = 0$,$\Delta=16m^{2}-24(2m^{2}-3)=72 - 32m^{2}>0$,$y_{1}y_{2}=\frac{2m^{2}-3}{6}$,$y_{1}+y_{2}=-\frac{2m}{3}$.
又$OA\perp OB$,所以$\overrightarrow{OA}\cdot\overrightarrow{OB}=y_{1}y_{2}+x_{1}x_{2}=0$,又$x=-y - m$,所以$y_{1}y_{2}+(-y_{1}-m)(-y_{2}-m)=0$,
整理得$2y_{1}y_{2}+(y_{1}+y_{2})m+m^{2}=0$,
即$2\times\frac{2m^{2}-3}{6}+(-\frac{2m}{3})m+m^{2}=0$,解得$m^{2}=1$,满足$72 - 32m^{2}>0$,
所以$m=\pm1$.
(3)$|AB|=\sqrt{(x_{1}-x_{2})^{2}+(y_{1}-y_{2})^{2}}=\sqrt{[(-y_{1}-m)-(-y_{2}-m)]^{2}+(y_{1}-y_{2})^{2}}=\sqrt{2(y_{1}-y_{2})^{2}}=\sqrt{2}\cdot\sqrt{(y_{1}+y_{2})^{2}-4y_{1}y_{2}}$.
当$m = 1$时,由
(2)得$y_{1}+y_{2}=-\frac{2}{3}$,$y_{1}y_{2}=-\frac{1}{6}$,所以$|AB|=\sqrt{2}\times\frac{\sqrt{10}}{3}=\frac{2\sqrt{5}}{3}$.
由对称性可知当$m=-1$时,也有$|AB|=\frac{2\sqrt{5}}{3}$. 所以$|AB|=\frac{2\sqrt{5}}{3}$.
11. [福建莆田2024高二期中]已知O为坐标原点,P是圆A:$(x + 2)^{2}+y^{2}=4$上任意一点,点B(2,0),线段BP的垂直平分线与直线AP交于点Q,记点Q的轨迹为曲线C.
(1)求曲线C的方程;
(2)设直线l与曲线C恰有一个公共点(在y轴右侧),且l与直线y = ±√3x分别交于M,N两点,求△BMN的面积S的最小值.
(1)求曲线C的方程;
(2)设直线l与曲线C恰有一个公共点(在y轴右侧),且l与直线y = ±√3x分别交于M,N两点,求△BMN的面积S的最小值.
答案:
解】
(1) 由题意可得,$||QA|-|QB|| = |AP| = 2<|AB| = 4$, 则点$Q$的轨迹为以$A$,$B$为焦点的双曲线. 设$C$的方程为$\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1(a>0,b>0)$,则$2a = 2$,$2c = |AB| = 4$,即$a = 1$,$c = 2$,所以$b=\sqrt{3}$, 所以曲线$C$的方程为$x^{2}-\frac{y^{2}}{3}=1$.
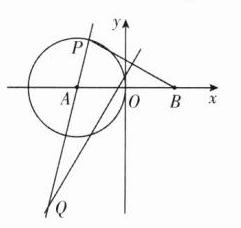
(2) 易知直线$l$的斜率不为$0$,则可设$l:x = my + n$,代入曲线$C$的方程得$(3m^{2}-1)y^{2}+6mny+3n^{2}-3 = 0$, 由已知得$3m^{2}-1\neq0$且$\Delta=36m^{2}n^{2}-4(3m^{2}-1)(3n^{2}-3)=0$,即$3m^{2}+n^{2}=1$. 将$x = my + n$,代入$x^{2}-\frac{y^{2}}{3}=0$得$(3m^{2}-1)y^{2}+6mny+3n^{2}=0$, 设$M(x_{1},y_{1})$,$N(x_{2},y_{2})$,则$y_{1}+y_{2}=\frac{-6mn}{3m^{2}-1}$,$y_{1}y_{2}=\frac{3n^{2}}{3m^{2}-1}$, 易知直线$l$与$x$轴的交点为$(n,0)$, 则$S=\frac{|2 - n|}{2}|y_{1}-y_{2}|=\frac{|2 - n|}{2}\cdot\sqrt{(y_{1}+y_{2})^{2}-4y_{1}y_{2}}=\frac{|2 - n|}{2}\cdot\frac{\sqrt{12n^{2}}}{|3m^{2}-1|}=\sqrt{3}|\frac{2}{n}-1|$. 由$3m^{2}+n^{2}=1$得$n^{2}\leq1$,即$-1\leq n\leq1$且$n\neq0$,则当$n = 1$时,$S$有最小值且最小值为$\sqrt{3}$.
解】
(1) 由题意可得,$||QA|-|QB|| = |AP| = 2<|AB| = 4$, 则点$Q$的轨迹为以$A$,$B$为焦点的双曲线. 设$C$的方程为$\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1(a>0,b>0)$,则$2a = 2$,$2c = |AB| = 4$,即$a = 1$,$c = 2$,所以$b=\sqrt{3}$, 所以曲线$C$的方程为$x^{2}-\frac{y^{2}}{3}=1$.

(2) 易知直线$l$的斜率不为$0$,则可设$l:x = my + n$,代入曲线$C$的方程得$(3m^{2}-1)y^{2}+6mny+3n^{2}-3 = 0$, 由已知得$3m^{2}-1\neq0$且$\Delta=36m^{2}n^{2}-4(3m^{2}-1)(3n^{2}-3)=0$,即$3m^{2}+n^{2}=1$. 将$x = my + n$,代入$x^{2}-\frac{y^{2}}{3}=0$得$(3m^{2}-1)y^{2}+6mny+3n^{2}=0$, 设$M(x_{1},y_{1})$,$N(x_{2},y_{2})$,则$y_{1}+y_{2}=\frac{-6mn}{3m^{2}-1}$,$y_{1}y_{2}=\frac{3n^{2}}{3m^{2}-1}$, 易知直线$l$与$x$轴的交点为$(n,0)$, 则$S=\frac{|2 - n|}{2}|y_{1}-y_{2}|=\frac{|2 - n|}{2}\cdot\sqrt{(y_{1}+y_{2})^{2}-4y_{1}y_{2}}=\frac{|2 - n|}{2}\cdot\frac{\sqrt{12n^{2}}}{|3m^{2}-1|}=\sqrt{3}|\frac{2}{n}-1|$. 由$3m^{2}+n^{2}=1$得$n^{2}\leq1$,即$-1\leq n\leq1$且$n\neq0$,则当$n = 1$时,$S$有最小值且最小值为$\sqrt{3}$.

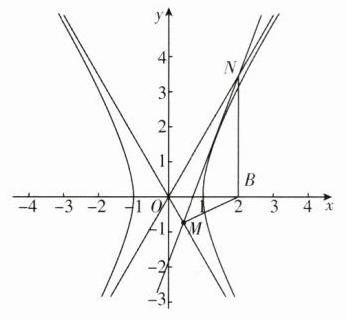
13. [南京大学2022强基计划]已知F,l为双曲线$\frac{(x - 4)^{2}}{4}-\frac{y^{2}}{12}=1$的右焦点与右准线,椭圆Γ以F和l为其对应的焦点及准线,过点F作一条平行于y = √3x的直线,交椭圆Γ于A,B两点,若Γ的中心位于以AB为直径的圆外,则椭圆离心率e的取值范围为________.
答案:
$(\sqrt{\frac{5 - \sqrt{13}}{3}},1)$ [解析]由双曲线方程可知其焦准距为3,则椭圆$\varGamma$的


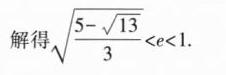
$(\sqrt{\frac{5 - \sqrt{13}}{3}},1)$ [解析]由双曲线方程可知其焦准距为3,则椭圆$\varGamma$的


14. [清华大学2023强基计划]已知抛物线C:x² = 4y,过点M(2,2)的直线交抛物线于A,B两点,过A,B两点作抛物线的切线交于点P,求△ABP面积S△ABP的最小值和点P的轨迹方程.
答案:


查看更多完整答案,请扫码查看


