《2024年高中必刷题高二数学选择性必修第一册人教B版》

1. [湖南株洲2024高二期中]直线$y = kx + 1$与椭圆$\frac{x^{2}}{5}+\frac{y^{2}}{m}=1$总有公共点,则实数$m$的取值范围是 （ ）
A. $(1,+\infty)$
B. $(0,5)\cup(5,+\infty)$
C. $[1,5)\cup(5,+\infty)$
D. $(0,1)\cup(1,5)$

答案： C 【解析】直线$y = kx + 1$过定点$(0,1)$，要满足该直线与椭圆总有公共点，则只需满足该点落在椭圆内或椭圆上，$\therefore\frac{0^{2}}{5}+\frac{1}{m}\leq1$，又$m ＞ 0$且$m\neq5$，$\therefore m\geq1$且$m\neq5$，故选 C.

2. 设抛物线$C:y^{2}=4x$的焦点为$F$,直线$l$过点$M(2,0)$且与$C$交于$A,B$两点,$|BF|=\frac{3}{2}$. 若$|AM|=\lambda|BM|$,则实数$\lambda =$ （ ）
A. $\frac{3}{2}$
B. 2
C. 4
D. 6

答案： C 【解析】由题意得抛物线的焦点为$F(1,0)$，准线方程为$x = - 1$，由$|BF|=\frac{3}{2}$及抛物线的定义知点$B$的横坐标为$\frac{1}{2}$，代入抛物线方程得$B(\frac{1}{2},\pm\sqrt{2})$.
根据抛物线的对称性，不妨取$B(\frac{1}{2},-\sqrt{2})$，则直线$l$的方程为$y=\frac{2\sqrt{2}}{3}(x - 2)$.
联立$\begin{cases}y=\frac{2\sqrt{2}}{3}(x - 2)\\y^{2}=4x\end{cases}$，得$A(8,4\sqrt{2})$，于是$\lambda=\frac{|AM|}{|BM|}=4$. 故选 C.

3. 如图,圆$F:(x - 1)^{2}+y^{2}=1$和抛物线$x=\frac{y^{2}}{4}$,过$F$的直线与抛物线和圆依次交于$A,B,C,D$四点,则$|AB|\cdot|CD|$的值是 （ ）


A. 1
B. 2
C. 3
D. 无法确定

答案： A 【解析】由题意知点$F(1,0)$既是圆$F$的圆心又是抛物线的焦点.
若直线的斜率不存在，则直线方程为$x = 1$，代入抛物线方程和圆的方程，可直接得到$A$，$B$，$C$，$D$四个点的坐标分别为$(1,2)$，$(1,1)$，$(1,-1)$，$(1,-2)$，所以$|AB| = 1$，$|CD| = 1$，从而$|AB|\cdot|CD| = 1$.
若直线的斜率存在，可设为$k$，又直线过点$F(1,0)$，则直线方程为$y = k(x - 1)$.
不妨设$A(x_{1},y_{1})$，$D(x_{2},y_{2})$，过点$A$，$D$分别作抛物线准线的垂线（图略），由抛物线的定义得$|AF| = x_{1}+1$，$|DF| = x_{2}+1$.
把直线方程与抛物线方程联立，消去$y$可得$k^{2}x^{2}-(2k^{2}+4)x + k^{2}=0$，$\Delta=(2k^{2}+4)^{2}-4k^{4}=16k^{2}+16＞0$，由一元二次方程根与系数的关系得$x_{1}x_{2}=1$.
因为$|BF| = |CF| = 1$，所以$|AB| = |AF|-|BF| = x_{1}$，$|CD| = |DF|-|CF| = x_{2}$，所以$|AB|\cdot|CD| = x_{1}x_{2}=1$. 综上，$|AB|\cdot|CD| = 1$，故选 A.

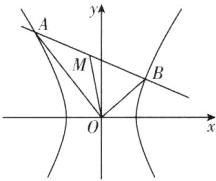
4. [山东新泰一中2024高二月考]不过原点的直线$l:y = kx + m(k\lt0,m\neq0)$与双曲线$E:\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1(a\gt0,b\gt0)$交于$A,B$两点,$M$为$AB$的中点,$O$为坐标原点. 若直线$OM$的斜率小于$\frac{3}{k}$,则双曲线$E$的离心率的取值范围为 （ ）
A. $(1,2)$
B. $(2,+\infty)$
C. $(\sqrt{2},2)$
D. $(\sqrt{2},+\infty)$

答案：
B 【解析】设点$A(x_{1},y_{1})$，$B(x_{2},y_{2})$，则有$\frac{x_{1}^{2}}{a^{2}}-\frac{y_{1}^{2}}{b^{2}}=1$，$\frac{x_{2}^{2}}{a^{2}}-\frac{y_{2}^{2}}{b^{2}}=1$，

两式作差得$\frac{x_{1}^{2}-x_{2}^{2}}{a^{2}}=\frac{y_{1}^{2}-y_{2}^{2}}{b^{2}}$，即$\frac{(x_{1}+x_{2})(x_{1}-x_{2})}{a^{2}}=\frac{(y_{1}+y_{2})(y_{1}-y_{2})}{b^{2}}$，
设$M(x_{0},y_{0})$，则有$x_{1}+x_{2}=2x_{0}$，$y_{1}+y_{2}=2y_{0}$，又$k_{OM}=\frac{y_{0}}{x_{0}}$，$k=\frac{y_{1}-y_{2}}{x_{1}-x_{2}}$，
代入整理得$k\cdot k_{OM}=\frac{b^{2}}{a^{2}}$，即$k_{OM}=\frac{b^{2}}{ka^{2}}$.
由题意知$\frac{b^{2}}{ka^{2}}＜\frac{3}{k}$，
因为$k＜0$，所以$\frac{b^{2}}{a^{2}}＞3$，$b^{2}＞3a^{2}$，
又$b^{2}=c^{2}-a^{2}$，所以$c^{2}-a^{2}＞3a^{2}$，
解得$c^{2}＞4a^{2}$，即$e^{2}＞4$，则$e＞2$.
故选 B.
【二级结论】如图，已知直线$l$与双曲线相交于$A$，$B$两点，点$M$为$AB$的中点，$O$为原点，则$k_{OM}\cdot k_{AB}=\frac{b^{2}}{a^{2}}=e^{2}-1$.

若直线$l$与双曲线的两条渐近线相交于$A$，$B$两点，其他条件不变，结论依然成立.

5. (多选) [江西师大附中2024高二期中]设$M$为双曲线$C:y^{2}-\frac{x^{2}}{3}=1$上一动点,$F_{1},F_{2}$分别为双曲线$C$的上、下焦点,$O$为坐标原点,则下列结论正确的是 （ ）
A. 若$|MF_{1}| = 4$,则$|MF_{2}| = 2$或6
B. 双曲线$C$与双曲线$D:\frac{x^{2}}{6}-\frac{y^{2}}{2}=-1$的离心率相同
C. 若点$Q(8,1)$,点$M$在双曲线$C$的上支,则$|MF_{2}|+|MQ|$的最小值为$2+\sqrt{65}$
D. 过$F_{1}$的直线$l$交$C$于不同的两点$G,H$,若$|GH| = 7$,则$l$有2条

答案：
ABC 【解析】对于 A，因为$a^{2}=1$，$b^{2}=3$，所以$a = 1$，$c=\sqrt{a^{2}+b^{2}}=\sqrt{1 + 3}=2$，则$|F_{1}F_{2}| = 2c = 4$，由双曲线的定义可知$||MF_{1}|-|MF_{2}|| = 2$，又$|MF_{1}| = 4$，则$|4-|MF_{2}|| = 2$，解得$|MF_{2}| = 2$或$6$. 当$|MF_{2}| = 2$时，$|MF_{1}|+|MF_{2}| = 4 + 2 = 6＞|F_{1}F_{2}| = 4$，符合题意；当$|MF_{2}| = 6$时，$|MF_{1}|+|MF_{2}| = 4 + 6 = 10＞|F_{1}F_{2}| = 4$，符合题意，
综上，$|MF_{2}| = 2$或$6$，故 A 正确.
对于 B，因为双曲线离心率$e=\frac{c}{a}=\frac{\sqrt{a^{2}+b^{2}}}{a}=\sqrt{1+\frac{b^{2}}{a^{2}}}$，所以双曲线$C:y^{2}-\frac{x^{2}}{3}=1$的离心率为$\sqrt{1+\frac{3}{1}} = 2$.
双曲线$D:\frac{x^{2}}{6}-\frac{y^{2}}{2}=-1$，即$\frac{y^{2}}{2}-\frac{x^{2}}{6}=1$，离心率为$\sqrt{1+\frac{6}{2}} = 2$，
所以双曲线$C$与双曲线$D:\frac{x^{2}}{6}-\frac{y^{2}}{2}=-1$的离心率相同，故 B 正确.
对于 C，$|MF_{2}|+|MQ| = 2+|MF_{1}|+|MQ|\geq2+|QF_{1}| = 2+\sqrt{65}$，当且仅当点$M$在线段$F_{1}Q$与双曲线的交点处时，等号成立，所以$|MF_{2}|+|MQ|$的最小值为$2+\sqrt{65}$，故 C 正确.
对于 D，由双曲线$C:y^{2}-\frac{x^{2}}{3}=1$，得$F_{1}(0,2)$，$F_{2}(0,-2)$，
当直线$l$的斜率为$0$时，$l$的方程为$y = 2$，联立$\begin{cases}y^{2}-\frac{x^{2}}{3}=1\\y = 2\end{cases}$，得$\begin{cases}x = 3\\y = 2\end{cases}$或$\begin{cases}x=-3\\y = 2\end{cases}$，所以$G(3,2)$，$H(-3,2)$，所以$|GH| = 6$，不符合题意；
当直线$l$的斜率不存在时，$|GH| = 2$，不符合题意，所以直线$l$的斜率存在且不为$0$.
故设$l:y = kx + 2$，$k\neq0$，设$G(x_{1},y_{1})$，$H(x_{2},y_{2})$，
联立$\begin{cases}y^{2}-\frac{x^{2}}{3}=1\\y = kx + 2\end{cases}$，得$(3k^{2}-1)x^{2}+12kx + 9 = 0$，则$\begin{cases}3k^{2}-1\neq0\\k\neq0\\\Delta＞0\\x_{1}+x_{2}=\frac{-12k}{3k^{2}-1}\\x_{1}x_{2}=\frac{9}{3k^{2}-1}\end{cases}$，
所以$|GH|=\sqrt{1 + k^{2}}\sqrt{(x_{1}+x_{2})^{2}-4x_{1}x_{2}}=\sqrt{1 + k^{2}}\sqrt{(\frac{-12k}{3k^{2}-1})^{2}-4\cdot\frac{9}{3k^{2}-1}}=\frac{6 + 6k^{2}}{|3k^{2}-1|}=7$，所以$6 + 6k^{2}=7(3k^{2}-1)$或$6 + 6k^{2}=7(1 - 3k^{2})$，
解得$k=\pm\frac{\sqrt{195}}{15}$或$k=\pm\frac{\sqrt{27}}{27}$，符合题意，所以这样的直线$l$有$4$条，故 D 错误. 故选 ABC.

6. (多选) [辽宁本溪一中2024高二期中]已知椭圆$C:\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1(a\gt b\gt0)$过点$(\sqrt{3},\frac{\sqrt{3}}{2})$,直线$l:y = -\frac{1}{2}x + m$与椭圆$C$交于$M,N$两点,且线段$MN$的中点为$P$,$O$为坐标原点,直线$OP$的斜率为$\frac{3}{2}$,则下列结论正确的是 （ ）
A. 椭圆$C$的离心率为$\frac{1}{2}$
B. 椭圆$C$的方程为$\frac{x^{2}}{12}+y^{2}=1$
C. 若$m = 1$,则$|MN|=\frac{3\sqrt{5}}{2}$
D. 若$m=\frac{1}{2}$,则椭圆$C$上存在$E,F$两点,使得$E,F$关于直线$l$对称

答案： AC 【解析】设$M(x_{1},y_{1})$，$N(x_{2},y_{2})$，则$P(\frac{x_{1}+x_{2}}{2},\frac{y_{1}+y_{2}}{2})$，即$k_{OP}=\frac{y_{1}+y_{2}}{x_{1}+x_{2}}=\frac{3}{2}$.
因为点$M$，$N$在椭圆$C$上，所以$\begin{cases}\frac{x_{1}^{2}}{a^{2}}+\frac{y_{1}^{2}}{b^{2}}=1\\\frac{x_{2}^{2}}{a^{2}}+\frac{y_{2}^{2}}{b^{2}}=1\end{cases}$两式相减，
得$\frac{(x_{1}+x_{2})(x_{1}-x_{2})}{a^{2}}+\frac{(y_{1}+y_{2})(y_{1}-y_{2})}{b^{2}}=0$，即$\frac{1}{a^{2}}+\frac{(y_{1}+y_{2})(y_{1}-y_{2})}{b^{2}(x_{1}+x_{2})(x_{1}-x_{2})}=0$，
由题得$k_{MN}=\frac{y_{1}-y_{2}}{x_{1}-x_{2}}=-\frac{1}{2}$，所以$\frac{1}{a^{2}}-\frac{3}{4b^{2}}=0$，即$b^{2}=\frac{3}{4}a^{2}$，又$a^{2}=b^{2}+c^{2}$，
所以$c^{2}=\frac{1}{4}a^{2}$，则离心率$e=\frac{c}{a}=\frac{1}{2}$，故 A 正确.
因为椭圆$C$过点$(\sqrt{3},\frac{\sqrt{3}}{2})$，所以$\frac{3}{a^{2}}+\frac{3}{4b^{2}}=1$，又由 A 选项知，$b^{2}=\frac{3}{4}a^{2}$，联立解得$a^{2}=4$，$b^{2}=3$，所以椭圆$C$的标准方程为$\frac{x^{2}}{4}+\frac{y^{2}}{3}=1$，故 B 错误.
若$m = 1$，则直线$l$的方程为$y=-\frac{1}{2}x + 1$，由$\begin{cases}y=-\frac{1}{2}x + 1\\\frac{x^{2}}{4}+\frac{y^{2}}{3}=1\end{cases}$得$x^{2}-x - 2 = 0$，所以$x_{1}=-1$，$x_{2}=2$，则$|MN|=\sqrt{1+(-\frac{1}{2})^{2}}\times|2 + 1|=\frac{3\sqrt{5}}{2}$，故 C 正确.
若$m=\frac{1}{2}$，则直线$l$的方程为$y=-\frac{1}{2}x+\frac{1}{2}$. 假设椭圆$C$上存在$E$，$F$两点，使得$E$，$F$关于直线$l$对称，则设$E(x_{3},y_{3})$，$F(x_{4},y_{4})$，线段$EF$的中点为$Q(x_{0},y_{0})$，则$x_{3}+x_{4}=2x_{0}$，$y_{3}+y_{4}=2y_{0}$. 因为$E$，$F$关于直线$l$对称，所以$k_{EF}=2$，且点$Q$在直线$l$上，即$y_{0}=-\frac{1}{2}x_{0}+\frac{1}{2}$. 又$E$，$F$两点在椭圆$C$上，所以$\begin{cases}\frac{x_{3}^{2}}{4}+\frac{y_{3}^{2}}{3}=1\\\frac{x_{4}^{2}}{4}+\frac{y_{4}^{2}}{3}=1\end{cases}$两式相减，得$\frac{(x_{3}+x_{4})(x_{3}-x_{4})}{4}+\frac{(y_{3}+y_{4})(y_{3}-y_{4})}{3}=0$，即$\frac{x_{3}+x_{4}}{4}+\frac{(y_{3}+y_{4})(y_{3}-y_{4})}{3(x_{3}-x_{4})}=0$，所以$y_{3}+y_{4}=-\frac{3(x_{3}+x_{4})}{8}$，即$y_{0}=-\frac{3}{8}x_{0}$. 联立$\begin{cases}y_{0}=-\frac{1}{2}x_{0}+\frac{1}{2}\\y_{0}=-\frac{3}{8}x_{0}\end{cases}$，解得$\begin{cases}x_{0}=4\\y_{0}=-\frac{3}{2}\end{cases}$，即$Q(4,-\frac{3}{2})$. 因为$\frac{4^{2}}{4}+\frac{(-\frac{3}{2})^{2}}{3}＞1$，所以点$Q$在椭圆$C$外，这与$Q$是弦$EF$的中点矛盾，所以椭圆$C$上不存在$E$，$F$两点，使得$E$，$F$关于直线$l$对称，故 D 错误.
故选 AC.

7. (多选)已知抛物线$C:y^{2}=2px(p\gt0)$的焦点$F(1,0)$,过$G(8,0)$的直线交抛物线于$A,B$两点,$O$为坐标原点,则以下说法正确的是 （ ）
A. $k_{OA}\cdot k_{OB}$为定值
B. 线段$AB$中点的轨迹方程为$y^{2}=2x - 16$
C. $|AF|+|BF|$的最小值为16
D. 点$O$在以$AB$为直径的圆外

答案： ABD 【解析】由题意可知$\frac{p}{2}=1$，所以$p = 2$，则抛物线方程$C:y^{2}=4x$. 易得直线$l$的斜率不为$0$，则可设直线$l$的方程为$x = my + 8$，$A(x_{1},y_{1})$，$B(x_{2},y_{2})$，所以$\begin{cases}x = my + 8\\y^{2}=4x\end{cases}$，得$y^{2}-4my - 32 = 0$，$\Delta＞0$，所以$y_{1}+y_{2}=4m$，$y_{1}y_{2}=-32$.
对于 A，$k_{OA}\cdot k_{OB}=\frac{y_{1}}{x_{1}}\cdot\frac{y_{2}}{x_{2}}=\frac{y_{1}}{\frac{y_{1}^{2}}{4}}\cdot\frac{y_{2}}{\frac{y_{2}^{2}}{4}}=\frac{4}{y_{1}}\cdot\frac{4}{y_{2}}=\frac{16}{y_{1}y_{2}}=-\frac{1}{2}$，故选项 A 正确；
对于 B，设线段$AB$的中点为$(x,y)$，
则有$x=\frac{x_{1}+x_{2}}{2}=\frac{\frac{y_{1}^{2}}{4}+\frac{y_{2}^{2}}{4}}{2}=\frac{(y_{1}+y_{2})^{2}-2y_{1}y_{2}}{8}=\frac{16m^{2}+64}{8}=2m^{2}+8$，
$y=\frac{y_{1}+y_{2}}{2}=2m$，所以满足$y^{2}=2x - 16$，故选项 B 正确；
对于 C，$|AF|+|BF|=x_{1}+\frac{p}{2}+x_{2}+\frac{p}{2}=\frac{y_{1}^{2}}{4}+1+\frac{y_{2}^{2}}{4}+1=\frac{y_{1}^{2}+y_{2}^{2}}{4}+2=\frac{(y_{1}+y_{2})^{2}-2y_{1}y_{2}}{4}+2=\frac{16m^{2}+64}{4}+2=4m^{2}+18\geq18$，当且仅当$m = 0$，即直线$l$垂直$x$轴时取等号，故选项 C 错误；
对于 D，$\overrightarrow{OA}\cdot\overrightarrow{OB}=x_{1}x_{2}+y_{1}y_{2}=\frac{y_{1}^{2}y_{2}^{2}}{16}+y_{1}y_{2}=64 - 32 = 32＞0$，则$O$在以$AB$为直径的圆外，所以选项 D 正确.
故选 ABD.

8. 已知$A,B$为椭圆$\frac{x^{2}}{9}+\frac{y^{2}}{5}=1$上两个不同的点,$F$为右焦点,$|AF|+|BF| = 4$. 若线段$AB$的垂直平分线交$x$轴于点$T$,则$|FT| =$________.

答案： $\frac{4}{3}$ 【解析】取椭圆方程为$\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1$，$c=\sqrt{a^{2}-b^{2}}$，直线方程为$x=\frac{a^{2}}{c}＞a$（椭圆右准线），椭圆上一点$P(x_{0},y_{0})$，右焦点$F(c,0)$，设点$P(x_{0},y_{0})$到直线$x=\frac{a^{2}}{c}$的距离为$d$，
则$\frac{|PF|}{d}=\frac{\sqrt{x_{0}^{2}+c^{2}-2cx_{0}+y_{0}^{2}}}{\frac{a^{2}}{c}-x_{0}}=\frac{c\sqrt{x_{0}^{2}+c^{2}-2cx_{0}+b^{2}-\frac{b^{2}x_{0}^{2}}{a^{2}}}}{a^{2}-x_{0}c}=\frac{c\sqrt{\frac{c^{2}}{a^{2}}x_{0}^{2}-2cx_{0}+a^{2}}}{a^{2}-x_{0}c}=\frac{c(a-\frac{c}{a}x_{0})}{a^{2}-x_{0}c}=\frac{c}{a}$，
所以$|PF|=\frac{c}{a}(\frac{a^{2}}{c}-x_{0})=a - ex_{0}$.
因为本题中椭圆的离心率$e=\frac{2}{3}$，设$A(x_{1},y_{1})$，$B(x_{2},y_{2})$，
则由上述焦半径公式得$(3-\frac{2}{3}x_{1})+(3-\frac{2}{3}x_{2})=4$，得$x_{1}+x_{2}=3$，
即$AB$的中点为$(\frac{3}{2},\frac{y_{1}+y_{2}}{2})$.
设$T(m,0)$. 由$k_{AB}=\frac{y_{1}-y_{2}}{x_{1}-x_{2}}$得线段$AB$垂直平分线的斜率为$-\frac{x_{1}-x_{2}}{y_{1}-y_{2}}$.
根据点$A$，$B$在椭圆上，则有$\frac{x_{1}^{2}}{9}+\frac{y_{1}^{2}}{5}=1$，$\frac{x_{2}^{2}}{9}+\frac{y_{2}^{2}}{5}=1$，作差化简得$y_{1}^{2}-y_{2}^{2}=\frac{5}{9}(x_{2}^{2}-x_{1}^{2})$，则线段$AB$的垂直平分线方程为$y=-\frac{x_{1}-x_{2}}{y_{1}-y_{2}}(x-\frac{3}{2})+\frac{y_{1}+y_{2}}{2}$，代入$T(m,0)$得$m-\frac{3}{2}=\frac{y_{1}^{2}-y_{2}^{2}}{2(x_{1}-x_{2})}=\frac{\frac{5}{9}(x_{2}^{2}-x_{1}^{2})}{2(x_{1}-x_{2})}=-\frac{\frac{5}{9}(x_{1}+x_{2})}{2}=-\frac{5}{6}$，
即$m=\frac{2}{3}$，则$|FT|=2-\frac{2}{3}=\frac{4}{3}$.

9. [江西南昌2024高二期中]已知平面上两点$M(-5,0)$和$N(5,0)$,若直线上存在点$P$使得$|PM|-|PN| = 6$,则称该直线为“单曲型直线”. 下列直线:①$y = x + 1$;②$y = 2$;③$y=\frac{4}{3}x$;④$y = 2x + 1$. 其中是“单曲型直线”的是________. (填序号)

答案： ①② 【解析】因为$|PM|-|PN| = 6＜10$，所以点$P$在以$M$，$N$为焦点的双曲线的右支上，即点$P$的轨迹方程为$\frac{x^{2}}{9}-\frac{y^{2}}{16}=1(x＞0)$. 根据题意得，“单曲型直线”与双曲线的右支存在交点，下面依次联立方程，消去$y$，判断所得方程有无正根即可.
对于①，联立$\begin{cases}\frac{x^{2}}{9}-\frac{y^{2}}{16}=1\\3y = x + 1\end{cases}$，得$15x^{2}-2x - 145 = 0$，因为$\Delta=(-2)^{2}-4\times15\times(-145)＞0$，且$x_{1}x_{2}＜0$，所以$3y = x + 1$是“单曲型直线”.
对于②，联立$\begin{cases}\frac{x^{2}}{9}-\frac{y^{2}}{16}=1\\y = 2\end{cases}$，得$x^{2}=\frac{45}{4}$，所以$y = 2$是“单曲型直线”.
对于③，联立$\begin{cases}\frac{x^{2}}{9}-\frac{y^{2}}{16}=1\\y=\frac{4}{3}x\end{cases}$，整理得$0 = 1$，显然不成立，所以$y=\frac{4}{3}x$不是“单曲型直线”.
对于④，联立$\begin{cases}\frac{x^{2}}{9}-\frac{y^{2}}{16}=1\\y = 2x + 1\end{cases}$，得$20x^{2}+36x + 153 = 0$，因为$\Delta=36^{2}-4\times20\times153＜0$，所以$y = 2x + 1$不是“单曲型直线”.
综上，是“单曲型直线”的有①②.