《2025年高中必刷题高二数学选择性必修第三册人教版》

1. 有4位教师分别在同一年级的4个班中担任数学老师,在数学测验时要求每位教师不能在本班监考,则监考的方法有 （ ）
A. 8种
B. 9种
C. 10种
D. 11种

答案： B 【解析】设 4 位监考教师分别为 A，B，C，D，所教班级分别为 a，b，c，d。假设 A 监考 b，则余下 3 人监考剩下的 3 个班，共有 3 种不同的方法。同理 A 监考 c，d 时，也分别有 3 种不同的方法。由分类加法计数原理得，监考方法共有 3 + 3 + 3 = 9（种）。

2. 从集合{3,5,7,9,11}中任取两个数作为a,b,可以得到不同的焦点在x轴上的椭圆方程$\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}} = 1$的个数为 （ ）
A. 25
B. 20
C. 10
D. 16

答案： C 【解析】焦点在 x 轴上的椭圆方程中，必有 a ＞ b，则 a 可取 5，7，9，11 共 4 个可能，b 可取 3，5，7，9 共 4 个可能。若 a = 5，则 b = 3，1 个椭圆；若 a = 7，则 b = 3，5，2 个椭圆；若 a = 9，则 b = 3，5，7，3 个椭圆；若 a = 11，则 b = 3，5，7，9，4 个椭圆。所以共有 1 + 2 + 3 + 4 = 10（个）椭圆。故选 C。

3. [湖北部分高中协作体2024高二联考]有3个旅游爱好者分别从4个不同的景点中选择一处游览,则不同的选择方法数为 （ ）
A. 81
B. 64
C. 24
D. 12

答案： B 【解析】3 个旅游爱好者分步去选择景点游览，有 4×4×4 = 64（种）不同的选择方法。故选 B。

4. [山东省实验中学2023高二期中]设集合A = {-1,0,1},集合B = {0,1,2,3},定义A * B = {(x,y)|x∈A∩B,y∈A∪B},则A * B的子集的个数是 （ ）
A. 5²
B. 2¹⁰
C. 2⁵
D. 10

答案： B 【解析】因为 A = {-1，0，1}，B = {0，1，2，3}，所以 A∪B = {-1，0，1，2，3}，A∩B = {0，1}，又 A * B = {(x，y)|x∈A∩B，y∈A∪B}，则 x 有 2 种情况，y 有 5 种情况，则由分步乘法计数原理可得 A * B 的元素有 2×5 = 10（个），所以 A * B 的子集的个数是 2¹⁰。故选 B。

5. [吉林部分学校2024高二期中联考]10 800的不同正因数的个数为 （ ）
A. 70
B. 60
C. 90
D. 80

答案： B 【解析】因为 10800 = 2⁴×3³×5²，则 10800 的每个因式由 m 个 2，n 个 3，t 个 5 相乘得到，其中 m∈{0，1，2，3，4}，n∈{0，1，2，3}，t∈{0，1，2}。
**避坑**：注意 m = 0，n = 0，t = 0 的情况不要漏掉，此时对应因式不含 2，3，5。所以 10800 的不同正因数的个数为 5×4×3 = 60。故选 B。

6. [安徽蚌埠2023高二期末]现用5种不同颜色对如图所示的四个部分进行涂色,要求相邻的两块不能用同一种颜色,则不同的涂色方法种数为________(用数字作答).

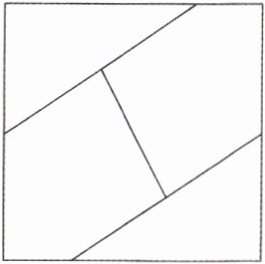
答案：
180 【解析】如图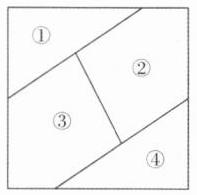标号。
由题意，①号涂色方案有 5 种，②号涂色方案有 4 种，③号涂色方案有 3 种，④号涂色方案有 3 种，故不同的涂色方案种数为 5×4×3×3 = 180。

7. [重庆八中2024高二期中]某单位有5位同事各有一辆私家车,车牌尾数分别是0,1,2,3,5,为遵守所在城市1月15日至18日4天的限行规定(奇数日车牌尾数为奇数的车通行,偶数日车牌尾数为偶数的车通行),5人商议拼车出行,每天任选一辆符合规定的车,但甲的车(车牌尾数为2)最多只能用一天,则不同的用车方案种数是 （ ）
A. 24
B. 27
C. 30
D. 33

答案： B 【解析】15 日至 18 日，有 2 天奇数日和 2 天偶数日，车牌尾数中有 3 个奇数和 2 个偶数。按日期分步，分 2 类，第一类，不用甲的车，有 3×1×3×1 = 9（种）不同的用车方案；第二类，甲的车只用 1 天，有 3×1×3×1×2 = 18（种）不同的用车方案。综上，共有 9 + 18 = 27（种）不同的用车方案。故选 B。

8. 用0,1,2,3,4,5这六个数字组成无重复数字的四位数,在组成的四位数中,能被5整除的有________个.

答案： 108 【解析】若个位为 0，则按照位数从高到低填上数字，共有 5×4×3 = 60（个）；若个位为 5，则千位不能为 0，有 4 种填法，百位和十位有 4×3 种填法，共有 4×4×3 = 48（种）填法。综上可得组成的四位数中，能被 5 整除的有 60 + 48 = 108（个）。

9. 教材变式[江苏连云港2024高二月考]用0,1,2,3,4这五个数字.
(1)可以组成多少个数字允许重复的三位数?
(2)可以组成多少个无重复数字的三位数?
(3)可以组成多少个无重复数字的三位偶数?

答案： 【解】（1）三位数的首位不能为 0，但可以有重复数字，首先考虑首位数字的选法，除 0 外共有 4 种选法，十位和个位可以排 0，因此，根据分步乘法计数原理共有 4×5×5 = 100（个）三位数。
（2）三位数的首位不能为 0，首先考虑首位数字的选法，除 0 外共有 4 种选法，十位可以排 0，除首位排的数字共有 4 种选法，个位除前两位排的数字共有 3 种选法，因此，根据分步乘法计数原理共有 4×4×3 = 48（个）无重复数字的三位数。
（3）偶数末位数字可取 0，2，4，因此，可以分两类：
一类是末位数字是 0，则有 4×3 = 12（个）三位偶数；
一类是末位数字不是 0，则末位有 2 种选法，即 2 或 4，再排首位，因为 0 不能在首位，所以有 3 种选法，十位有 3 种选法，因此有 2×3×3 = 18（个）三位偶数。
综上，共有 12 + 18 = 30（个）三位偶数，即可以组成 30 个无重复数字的三位偶数。

10. 甲、乙、丙、丁4名同学争夺数学、物理、化学3门学科知识竞赛的冠军,且每门学科只有1名冠军产生,则不同的冠军获得情况共有________种.

答案： 64 【解析】由题知，研究的对象是“3 门学科”，只有 3 门学科各产生 1 名冠军，才算完成了这件事，而 4 名同学不一定每人都能获得冠军，故完成这件事分三步。
第一步，产生第 1 门学科冠军，它一定被其中 1 名同学获得，故有 4 种不同的获得情况；
第二步，产生第 2 门学科冠军，因为夺得第 1 个学科冠军的同学还可以去争夺第 2 个学科的冠军，所以第 2 个学科冠军也是由 4 名同学去争夺，有 4 种不同的获得情况；
第三步，产生第 3 门学科冠军，同理，也有 4 种不同的获得情况。
由分步乘法计数原理知，不同的冠军获得情况共有 4×4×4 = 64（种）。

11. 某外语小组有9人,每人至少会英语和日语中的一门,其中7人会英语,3人会日语.从中选出会英语和日语的各一人组成一个二人活动小组,有________种选法.

答案： 20 【解析】因为 7 + 3 - 9 = 1，所以外语小组 9 人中有 1 人既会英语又会日语。分三类：①当既会英语又会日语的人当选为会英语的人时，选出只会日语的一人即可，有 2 种选法；②当既会英语又会日语的人当选为会日语的人时，选出只会英语的一人即可，有 6 种选法；③当既会英语又会日语的人没被选出时，则需从只会日语和只会英语的人中各选出一人，有 2×6 = 12（种）选法。故共有 2 + 6 + 12 = 20（种）选法。