《2024年高中必刷题高二数学选择性必修第一册人教B版》

1. [山东新泰一中2024高二期末]已知直线l经过点A(-6,4)，斜率为$\frac{4}{3}$，则直线l在x轴上的截距为 ( )
A. -9
B. 9
C. -12
D. 12

答案： A 【解析】由直线l经过点A(-6,4),斜率为$\frac{4}{3}$,可得直线l的方程为y - 4 = $\frac{4}{3}$(x + 6),即4x - 3y + 36 = 0,令y = 0,可得x = -9,故直线l在x轴上的截距为-9.故选A.

2. 经过点(1,2)，且倾斜角为45°的直线方程是 ( )
A. y=x-3
B. y=x+1
C. y=-(x-3)
D. y=-(x+3)

答案： B 【解析】因为所求直线的倾斜角为45°,所以所求直线的斜率k = tan 45° = 1,所以直线方程为y - 2 = x - 1,即y = x + 1,故A,C,D错误.故选B.

3. 过点P(1,1)且方向向量为(-1,3)的直线方程为 ( )
A. y=-3x-4
B. y=-3x+4
C. y=3x+2
D. y=3x-2

答案： B 【解析】因为直线的方向向量为(-1,3),所以直线的斜率k = $\frac{3}{-1}$ = -3.又直线过点P(1,1),所以直线方程为y - 1 = -3(x - 1),即y = -3x + 4.故选B.

4. [湖北武汉部分重点中学2024高二期中联考]一束光线从点A(-$\sqrt{3}$,3)射出，沿倾斜角为150°的直线射到x轴上，经x轴反射后，反射光线所在的直线方程为 ( )
A. y=$\sqrt{3}$x-2
B. y=-$\sqrt{3}$x+2
C. y=-$\frac{\sqrt{3}}{3}$x+2
D. y=$\frac{\sqrt{3}}{3}$x-2

答案： D 【解析】倾斜角为150°的直线,斜率为tan 150° = -$\frac{\sqrt{3}}{3}$,所以入射光线所在的直线方程为y - 3 = -$\frac{\sqrt{3}}{3}$(x + $\sqrt{3}$) = -$\frac{\sqrt{3}}{3}$x - 1,即y = -$\frac{\sqrt{3}}{3}$x + 2.令y = 0,解得x = 2$\sqrt{3}$,所以入射光线与x轴的交点为(2$\sqrt{3}$,0).又由题意知反射光线所在直线的斜率为$\frac{\sqrt{3}}{3}$,故反射光线所在直线的方程为y - 0 = $\frac{\sqrt{3}}{3}$(x - 2$\sqrt{3}$),即y = $\frac{\sqrt{3}}{3}$x - 2.故选D.

5. [广东江门台山第一中学2024高二期中]直线y+2=$\frac{\sqrt{3}}{3}$(x-4$\sqrt{3}$)的倾斜角及在y轴上的截距分别是 ( )
A. $\frac{\pi}{6}$，6
B. $\frac{\pi}{6}$，-6
C. $\frac{\pi}{3}$，6
D. $\frac{\pi}{3}$，-6

答案： B 【解析】由直线y + 2 = $\frac{\sqrt{3}}{3}$(x - 4$\sqrt{3}$)可得其斜率k = $\frac{\sqrt{3}}{3}$,设直线的倾斜角为θ,则tan θ = $\frac{\sqrt{3}}{3}$.因为θ∈[0,π),所以θ = $\frac{π}{6}$,即倾斜角为$\frac{π}{6}$.当x = 0时,y + 2 = $\frac{\sqrt{3}}{3}$×(-4$\sqrt{3}$) = -4,得y = -6,所以直线在y轴上的截距为-6,故选B.

6. y=ax+$\frac{1}{a}$(a＞0)表示的直线可能是 ( )

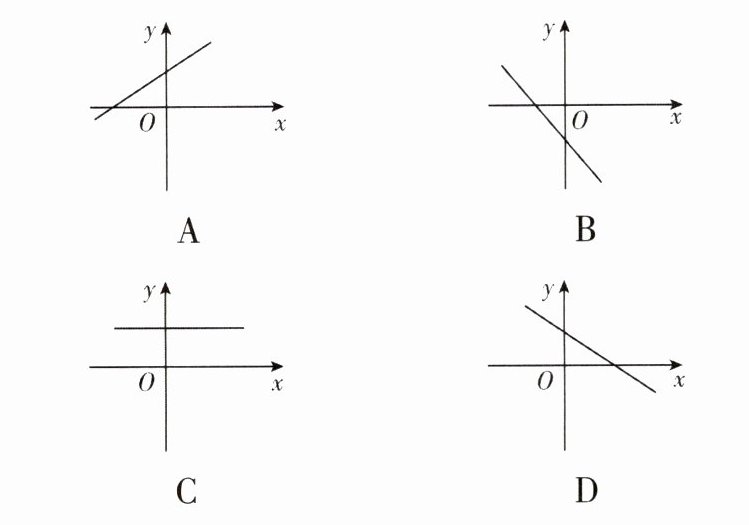
答案： A 【解析】当a＞0时,直线y = ax + $\frac{1}{a}$的斜率a＞0,该直线在y轴上的截距$\frac{1}{a}$＞0,故选A.

7. 若直线l经过点P(2,3)，且在x轴上的截距的取值范围是(-1,3)，则其斜率k的取值范围是 ( )
A. (-∞,-3)∪(1,+∞)
B. (-1,$\frac{1}{3}$)
C. (-3,1)
D. (-∞,-1)∪($\frac{1}{3}$,+∞)

答案： A 【解析】取x轴上的点M(-1,0),N(3,0),则$k_{PM}$ = $\frac{3 - 0}{2 - (-1)}$ = 1,$k_{PN}$ = $\frac{3 - 0}{2 - 3}$ = -3.
∵直线l与线段MN相交(不包含端点),
∴k＜-3或k＞1.

8. [山东济南2024高二月考]直线l的方程为y-a=(a-1)(x+2)，若直线l在y轴上的截距为6，则a=________。

答案： $\frac{8}{3}$ 【解析】直线l的方程可化为y = (a - 1)x + 3a - 2,由直线l在y轴上的截距为6,可得3a - 2 = 6,解得a = $\frac{8}{3}$.

9. [广东深圳2024高二期中]经过两点(x₁,y₁)，(x₂,y₂)的直线方程可以表示为 ( )
A. $\frac{x-x₁}{x₂-x₁}$=$\frac{y-y₁}{y₂-y₁}$
B. $\frac{x-x₂}{x₁-x₂}$=$\frac{y-y₂}{y₁-y₂}$
C. (y-y₁)(x₂-x₁)=(x-x₁)(y₂-y₁)
D. y-y₁=$\frac{y₂-y₁}{x₂-x₁}$(x-x₁)

答案： C 【解析】当经过$(x_{1},y_{1}),(x_{2},y_{2})$的直线不与x轴、y轴平行时,所有直线均可以用$\frac{x - x_{2}}{x_{1} - x_{2}}$ = $\frac{y - y_{2}}{y_{1} - y_{2}}$表示,由于$x_{1},x_{2}$可能相等,$y_{1},y_{2}$也可能相等,所以只有选项C满足包括与x轴、y轴平行的直线.故选C.

10. [江苏盐城2024高二期中]已知点A(-2,4)，B(4,-1)，则直线AB在y轴上的截距为 ( )
A. $\frac{8}{3}$
B. $\frac{7}{3}$
C. $\frac{14}{5}$
D. $\frac{13}{5}$

答案： B 【解析】因为直线经过两点A(-2,4)和B(4,-1),所以直线AB的方程为$\frac{y + 1}{4 + 1}$ = $\frac{x - 4}{-2 - 4}$,化简得5x + 6y - 14 = 0,令x = 0,则y = $\frac{7}{3}$,所以直线AB在y轴上的截距为$\frac{7}{3}$.故选B.