《2024年高中必刷题高二数学选择性必修第一册人教B版》

1. [四川成都第七中学2023高二月考]已知圆$O:x^{2}+y^{2}=1$,点$A(x_{0},0)(x_{0}\geq0)$,动圆$M$经过点$A$且与圆$O$相切,记动圆圆心$M$的轨迹为$E$,有下列几个命题：
①若$x_{0}=0$,则轨迹$E$表示圆;②若$0＜x_{0}＜1$,则轨迹$E$表示椭圆;③若$x_{0}=1$,则轨迹$E$表示抛物线;④若$x_{0}＞1$,则轨迹$E$表示双曲线. 其中,真命题的个数为 ( )
A. 1
B. 2
C. 3
D. 4

答案： C 【解析】设动圆M的圆心坐标为(x,y),半径为r,当$x_{0}=0$时,动圆M与圆O内切,故$|MO| = 1 - r$,即$|MO| = 1 - |MO|$,$|MO|=\frac{1}{2}$,轨迹E为圆,①为真命题;
当$0＜x_{0}＜1$时,动圆M与圆O内切,故$|MO| = 1 - r$,即$|MO|+|MA| = 1＞|AO|$,故轨迹E为椭圆,②为真命题;
当$x_{0}=1$时,其中一种情况为动圆M与圆O内切,且圆M在圆O内,此时,$|MO| = 1 - r$,$|MO|+|MA| = 1 = |AO|$,轨迹E为线段OA,不是抛物线,③为假命题;
当$x_{0}＞1$时,动圆M与圆O外切,$|MO| = 1 + r$,即$|MO|-|MA| = 1＜|AO|$,所以轨迹E为双曲线的右支,当动圆M与圆O内切,圆O在圆M内时,$|MO| = r - 1$,$|MA|-|MO| = 1＜|AO|$,所以轨迹E为双曲线的左支,④为真命题. 故选C.

2. [山东新泰一中2024高二月考]已知抛物线$C:y^{2}=2px(p＞0)$,点$M$在$C$上,直线$l:2x - y + 6 = 0$与$x$轴、$y$轴分别交于$A,B$两点. 若$\triangle AMB$面积的最小值为$\frac{15}{2}$,则$p=$ ( )
A. 44
B. 4
C. 4或44
D. 1或4

答案： B 【解析】由题意可得$A(-3,0)$,$B(0,6)$,设点M到直线l的距离为d,由$|AB| = 3\sqrt{5}$,$(S_{\triangle AMB})_{min}=\frac{15}{2}$,可得$d_{min}=\sqrt{5}$. 设$M(\frac{y_{0}^{2}}{2p},y_{0})$,
则$d=\frac{|\frac{y_{0}^{2}}{p}-y_{0}+6|}{\sqrt{5}}=\frac{|\frac{1}{p}(y_{0}-\frac{p}{2})^{2}-\frac{p}{4}+6|}{\sqrt{5}}$,
故当$y_{0}=\frac{p}{2}$时,d有最小值,$d_{min}=\frac{|6 - \frac{p}{4}|}{\sqrt{5}}=\sqrt{5}$,解得$p = 4$或$p = 44$.
由题意,点M到直线AB的距离存在最小值,故$p = 4$.
故选B.

3. [江西南昌二中2024高二期中]已知$M$是抛物线$x^{2}=8y$的对称轴和准线的交点,点$N$是其焦点,点$P$在该抛物线上,且满足$|PM| = m|PN|$,则实数$m$的最大值为 ( )
A. 2
B. $\sqrt{3}$
C. $\frac{3}{2}$
D. $\sqrt{2}$

答案：
D 【解析】易知$N(0,2)$,$M(0,-2)$,如图所示,过P作PA垂直于准线,垂足为点A,

由抛物线定义知$|PA| = |PN|$,则$\frac{|PM|}{|PN|}=m=\frac{|PM|}{|PA|}=\frac{1}{\sin\angle PMA}$.
易知当直线PM与抛物线相切时$\angle PMA$最小,此时m取得最大值.
不妨设$l_{PM}:y = kx - 2$,与抛物线方程联立得$x^{2}-8kx + 16 = 0$,则$\Delta=(-8k)^{2}-16\times4 = 0$,解得$k=\pm1$,
此时可知$\angle PMA = 45^{\circ}$,则$m=\frac{1}{\sin\angle PMA}=\sqrt{2}$. 故选D.

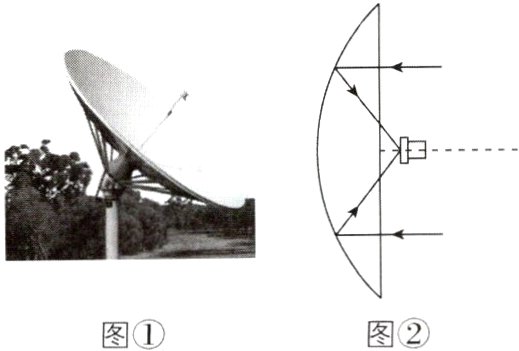
4. [江苏常州2024高二期中]某学习小组研究一种卫星接收天线(如图①所示),发现其曲面与轴截面的交线为抛物线,在轴截面内的卫星波束呈近似平行状态射入形为抛物线的接收天线,经反射聚焦到焦点处(如图②所示). 已知接收天线的口径(直径)为3.6 m,深度为0.6 m,则该抛物线的焦点到顶点的距离为 ( )

A. 1.35 m
B. 2.05 m
C. 2.7 m
D. 5.4 m

答案：
A 【解析】如图所示,在接收天线的轴截面所在平面上建立平面直角坐标系Oxy,使接收天线的顶点(即抛物线的顶点)与原点O重合,焦点F在x轴上.
设抛物线的标准方程为$y^{2}=2px(p＞0)$. 由已知条件可得,点$A(0.6,1.8)$在抛物线上,所以$1.2p = 1.8^{2}$,解得$p = 2.7$,因此该抛物线的焦点到顶点的距离为1.35 m,故选A.

5. (多选)在平面直角坐标系$xOy$中,点$F$是抛物线$C:y^{2}=ax(a＞0)$的焦点,点$A(\frac{a}{2},1),B(a,b)(b＞0)$在抛物线$C$上,则下列结论正确的是 ( )
A. $C$的准线方程为$x = -\frac{\sqrt{2}}{4}$
B. $b = \sqrt{2}$
C. $\overrightarrow{OA}\cdot\overrightarrow{OB}=2$
D. $\frac{1}{|AF|}+\frac{1}{|BF|}=\frac{16\sqrt{2}}{15}$

答案： ABD 【解析】点$A(\frac{a}{2},1)(a＞0)$,$B(a,b)(b＞0)$在抛物线C上,
则有$\begin{cases}1^{2}=\frac{a^{2}}{2}\\b^{2}=a^{2}\end{cases}$,解得$\begin{cases}a=\sqrt{2}\\b=\sqrt{2}\end{cases}$.
所以抛物线$C:y^{2}=\sqrt{2}x$,$A(\frac{\sqrt{2}}{2},1)$,$B(\sqrt{2},\sqrt{2})$.
选项A:抛物线C的准线方程为$x = -\frac{\sqrt{2}}{4}$,A正确;
选项B:$b=\sqrt{2}$,B正确;
选项C:$\overrightarrow{OA}\cdot\overrightarrow{OB}=\frac{\sqrt{2}}{2}\times\sqrt{2}+1\times\sqrt{2}=1+\sqrt{2}$,C错误;
选项D:抛物线C的焦点$F(\frac{\sqrt{2}}{4},0)$,则$|AF|=\sqrt{(\frac{\sqrt{2}}{4}-\frac{\sqrt{2}}{2})^{2}+(0 - 1)^{2}}=\frac{3\sqrt{2}}{4}$,$|BF|=\sqrt{(\frac{\sqrt{2}}{4}-\sqrt{2})^{2}+(0-\sqrt{2})^{2}}=\frac{5\sqrt{2}}{4}$,则$\frac{1}{|AF|}+\frac{1}{|BF|}=\frac{2\sqrt{2}}{3}+\frac{2\sqrt{2}}{5}=\frac{16\sqrt{2}}{15}$,D正确. 故选ABD.
【特别注意】注意$\frac{1}{|AF|}+\frac{1}{|BF|}$不能运用公式$\frac{1}{|AF|}+\frac{1}{|BF|}=\frac{2}{p}$求得,因为此时AB不是焦点弦($A,F,B$不在一条直线上).

6. 如图,正方形$ABCD$和正方形$DEFG$的边长分别为$a,b(a ＜ b)$,原点$O$为边$AD$的中点,抛物线$y^{2}=2px(p＞0)$经过$C,F$两点,则$\frac{b}{a}=$________.

答案： $1+\sqrt{2}$【解析】由题意知,点C的坐标为$(\frac{a}{2},-a)$,点F的坐标为$(\frac{a}{2}+b,b)$.
$\because C,F$两点都在抛物线$y^{2}=2px$上,
$\therefore\begin{cases}a^{2}=2p\cdot\frac{a}{2}\\b^{2}=2p\cdot(\frac{a}{2}+b)\end{cases}$,即$a^{2}-b^{2}+2ab = 0$,即$1-(\frac{b}{a})^{2}+\frac{2b}{a}=0$,解得$\frac{b}{a}=1+\sqrt{2}$或$\frac{b}{a}=1-\sqrt{2}$.$\because0＜a＜b$,$\therefore\frac{b}{a}=1+\sqrt{2}$.

7. [山东济南历城第二中学2023高二期中]抛物线$E:x^{2}=4y$与圆$M:x^{2}+(y - 1)^{2}=25$交于$A,B$两点,圆心$M(0,1)$,点$P$为劣弧$AB$上不同于$A,B$的一个动点,平行于$y$轴的直线$PN$交抛物线于点$N$,则$\triangle PMN$周长的取值范围是________.

答案：
$(10,12)$【解析】$\because$圆$M:x^{2}+(y - 1)^{2}=25$,抛物线$E:x^{2}=4y$,$\therefore$圆心

8. 已知抛物线$C:y^{2}=2px(p＞0)$的焦点为$F$,准线为$l$. 若位于$x$轴上方的动点$A$在准线$l$上,线段$AF$与抛物线$C$相交于点$B$,且$\frac{|AF|}{|BF|}-|AF| = 1$,则抛物线$C$的标准方程为________.

答案：

9. 抛物线的聚焦特点:从抛物线的焦点发出的光经过抛物线反射后,光线都平行于抛物线的对称轴. 另一方面,根据光路的可逆性,平行于抛物线对称轴的光线射向抛物线后的反射光线都会汇聚到抛物线的焦点处. 已知抛物线$y^{2}=2px(p＞0)$,一条平行于抛物线对称轴的光线从点$A(3,1)$向左发出,先经抛物线反射,再经直线$y = x - 3$反射后,恰好经过点$A$,则该抛物线的标准方程为________.

答案：