《2024年高中必刷题高二数学选择性必修第一册人教B版》

12. [湖北武汉部分重点中学2024高二期中联考]已知圆$C:(x - 1)^{2}+(y - 2)^{2}=25$，直线$l:mx - y - 3m + 1 = 0$与圆$C$相交于$A$，$B$两点，则$|AB|$的最小值为（ ）
A. $4\sqrt{5}$
B. 2
C. 4
D. $2\sqrt{5}$

答案：
A　[解析]由圆C的方程可得圆心C(1,2)，半径r = 5，直线l的方程可整理为m(x - 3)-y + 1 = 0，令$\begin{cases}x - 3 = 0\\-y + 1 = 0\end{cases}$， 解得$\begin{cases}x = 3\\y = 1\end{cases}$，所以直线l恒过定点D(3,1)。
由题意知，当AB与CD垂直时，弦长|AB|最小，又$k_{CD}=\frac{2 - 1}{1 - 3}=-\frac{1}{2}$，$k_{AB}=m$，所以此时m = 2，直线l:2x - y - 5 = 0，点C到直线l的距离d = $\frac{|2 - 2 - 5|}{\sqrt{4 + 1}}$ = $\sqrt{5}$，所以|AB|$_{min}$ = 2$\sqrt{r^{2}-d^{2}}$ = 2$\sqrt{25 - 5}$ = 4$\sqrt{5}$。 故选A。

13. [安徽六安舒城中学2023高二期中]不论$m$为何实数，直线$(2m + 1)x+(m + 1)y - m - 1 = 0$与圆$x^{2}+y^{2}-2ax + a^{2}-2a - 4 = 0$恒有公共点，则实数$a$的取值范围是（ ）
A. $[-2,2]$
B. $[0,2]$
C. $[-1,3]$
D. $[1,3]$

答案： C　[解析]由$x^{2}+y^{2}-2ax + a^{2}-2a - 4 = 0$，得(x - a)² + $y^{2}=2a + 4$，则2a + 4＞0，得a ＞ -2。
由(2m + 1)x+(m + 1)y - m - 1 = 0，得m(2x + y - 1)+(x + y - 1)=0，由$\begin{cases}2x + y - 1 = 0\\x + y - 1 = 0\end{cases}$， 解得$\begin{cases}x = 0\\y = 1\end{cases}$，所以直线(2m + 1)x+(m + 1)y - m - 1 = 0恒过定点(0,1)。
因为直线(2m + 1)x+(m + 1)y - m - 1 = 0与圆$x^{2}+y^{2}-2ax + a^{2}-2a - 4 = 0$恒有公共点，所以点(0,1)在圆内或圆上，所以0² + 1² - 0 + $a^{2}-2a - 4\leqslant0$，即$a^{2}-2a - 3\leqslant0$，解得 - 1≤a≤3。
综上，a∈[-1,3]。 故选C。

14. [北京第十五中学2024高二期中]已知直线$y = 2 + k(x - 1)$与曲线$y = \sqrt{1 - x^{2}}$有两个公共点，则实数$k$的取值范围是（ ）
A. $(\frac{3}{4},1]$
B. $(0,\frac{3}{4})$
C. $(\frac{5}{12},1]$
D. $(\frac{5}{12},\frac{3}{4})$

答案：
A　[解析]由y = $\sqrt{1 - x^{2}}$可得$x^{2}+y^{2}=1(y\geqslant0)$，所以曲线y = $\sqrt{1 - x^{2}}$为半圆，又由直线y = 2 + k(x - 1)可得，直线恒过定点A(1,2)，记B(-1,0)。 当直线y = 2 + k(x - 1)与半圆$x^{2}+y^{2}=1(y\geqslant0)$相切时，圆心到直线的距离为d = $\frac{|2 - k|}{\sqrt{k^{2}+1}}$ = 1，解得k = $\frac{3}{4}$，又$k_{AB}=1$，如图所示，当$\frac{3}{4}＜k\leqslant1$时，直线y = 2 + k(x - 1)与曲线y = $\sqrt{1 - x^{2}}$有两个公共点。 故选A。

15. [吉林东北师大附中2023高二期末]已知圆$C:x^{2}+y^{2}-2y - 4 = 0$，直线$l:mx - y + 1 - m = 0$.
(1)写出圆$C$的圆心坐标和半径，并判断直线$l$与圆$C$的位置关系；
(2)若直线$l$与圆$C$交于两点$A$，$B$，且$|AB| = 3\sqrt{2}$，求直线$l$的方程.

答案： [解]
(1)$x^{2}+y^{2}-2y - 4 = 0$整理得$x^{2}+(y - 1)^{2}=5$，故圆C的圆心坐标为(0,1)，半径为$\sqrt{5}$。
mx - y + 1 - m = 0可变形为y - 1 = m(x - 1)，故直线l过定点M(1,1)。
因为1²+(1 - 1)² = 1 ＜ 5，故点M(1,1)在圆C内，所以直线l与圆C相交。
(2)圆心(0,1)到l:mx - y + 1 - m = 0的距离d = $\frac{|-1 + 1 - m|}{\sqrt{m^{2}+1}}$ = $\frac{|m|}{\sqrt{m^{2}+1}}$，所以$d^{2}+(\frac{|AB|}{2})^{2}=5$，解得m = ±1，故直线l的方程为x - y = 0或x + y - 2 = 0。

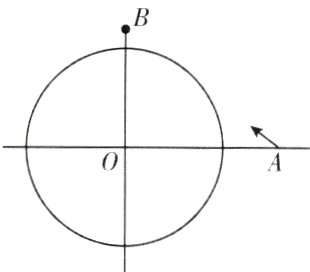
16. 如图，已知一艘停在海面上的海监船$O$上配有雷达，其监测范围是半径为25 km的圆形区域，一艘轮船从位于海监船正东40 km的$A$处出发，径直驶向位于海监船正北30 km的$B$处岛屿，速度为28 km/h，则这艘轮船能被海监船监测到的时长为（ ）

A. 1 h
B. 0.75 h
C. 0.5 h
D. 0.25 h

答案：
C　[解析]如图，以O为坐标原点，东西方向为x轴建立如图所示的平面直角坐标系，连接AB。
则A(40,0)，B(0,30)，圆O方程为$x^{2}+y^{2}=25^{2}$，直线AB的方程为$\frac{x}{40}+\frac{y}{30}=1$，即3x + 4y - 120 = 0。
设点O到直线AB的距离为d，则d = $\frac{|-120|}{5}$ = 24 ＜ 25，所以该艘轮船能被海监船监测到。 设监测到的时长为t，则t = $\frac{2\sqrt{25^{2}-24^{2}}}{28}$ = 0.5 h，因此该艘轮船能被海监船监测到的时长是0.5 h。 故选C。

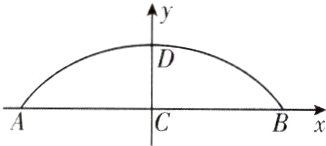
17. [河北石家庄2024高二期中]如图，这是某圆弧形山体隧道的示意图，其中底面$AB$的长为16米，最大高度$CD$的长为4米，以$C$为坐标原点，$AB$所在的直线为$x$轴建立平面直角坐标系.
(1)求该圆弧所在圆的方程.
(2)若某种汽车的宽约为2.5米，高约为1.6米，车辆行驶时两车的间距要求不小于0.5米以保证安全，同时车顶不能与隧道有剐蹭，则该隧道最多可以并排通过多少辆该种汽车?（将汽车看作长方体）

答案： [解]
(1)由圆的对称性可知，该圆弧所在圆的圆心在y轴上，设圆心为(0,b)。
设该圆的半径为r米，则$r^{2}=8^{2}+(r - 4)^{2}$，解得r = 10，因此b = -(10 - 4)= - 6，故该圆弧所在圆的方程为$x^{2}+(y + 6)^{2}=100$。
(2)设与该种汽车等高且能通过该隧道的最大宽度为d米，则$(\frac{d}{2})^{2}+(6 + 1.6)^{2}=10^{2}$，解得d = 2$\sqrt{42.24}$。
若并排通过5辆该种汽车，则安全通行的宽度应为5×2.5 + 4×0.5 = 14.5＞2$\sqrt{42.24}$，故该隧道不能并排通过5辆该种汽车。
若并排通过4辆该种汽车，则安全通行的宽度应为4×2.5 + 3×0.5 = 11.5＜2$\sqrt{42.24}$，则隧道能并排通过4辆该种汽车。
综上所述，该隧道最多可以并排通过4辆该种汽车。

18. [陕西西安长安区一中2024开学考试]已知圆$C$的方程为$x^{2}+y^{2}=1$.
(1)求过点$P(1,2)$且与圆$C$相切的直线$l$的方程；
(2)直线$m$过点$P(1,2)$，且与圆$C$交于$A$，$B$两点，若$|AB|=\sqrt{2}$，求直线$m$的方程.

答案： [解]
(1)根据题意，得点P在圆C外，分两种情况讨论：
当直线l的斜率不存在时，过点P(1,2)的直线方程是x = 1，与圆C:$x^{2}+y^{2}=1$相切，满足题意；
当直线l的斜率存在时，设直线l的方程为y - 2 = k(x - 1)，即kx - y - k + 2 = 0，因为直线l与圆C相切，所以圆心(0,0)到直线l的距离为$\frac{|2 - k|}{\sqrt{k^{2}+1}}$ = 1，解得k = $\frac{3}{4}$，此时，直线l的方程为3x - 4y + 5 = 0。
所以满足条件的直线l的方程是x = 1或3x - 4y + 5 = 0。
(2)根据题意，若|AB| = $\sqrt{2}$，则圆心到直线m的距离d = $\sqrt{1^{2}-(\frac{|AB|}{2})^{2}}$ = $\frac{\sqrt{2}}{2}$，结合
(1)知直线m的斜率一定存在。
设直线m的方程为y - 2 = n(x - 1)，即nx - y - n + 2 = 0，则d = $\frac{|2 - n|}{\sqrt{n^{2}+1}}$ = $\frac{\sqrt{2}}{2}$，解得n = 1或n = 7。
所以满足条件的直线m的方程是x - y + 1 = 0或7x - y - 5 = 0。
[易错警示]求过某点的圆的切线问题时，应先确定该点与圆的位置关系，再求直线方程。若点在圆内，则过该点的切线不存在；若点在圆上，则过该点的切线只有一条；若点在圆外，则过该点的切线有两条，此时应考虑切线斜率不存在的情况。