2024年高中必刷题高二数学选择性必修第一册人教B版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2024年高中必刷题高二数学选择性必修第一册人教B版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第15页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
1. 正三棱锥A - BCD的所有棱长都相等,则侧棱与底面所成的角的正切值是 ( )
A. $\sqrt{3}$
B. $\sqrt{2}$
C. $\frac{\sqrt{3}}{3}$
D. $\frac{\sqrt{2}}{2}$
A. $\sqrt{3}$
B. $\sqrt{2}$
C. $\frac{\sqrt{3}}{3}$
D. $\frac{\sqrt{2}}{2}$
答案:
B 【解析】设正三棱锥A - BCD的底面正三角形BCD的中心为O,棱长为a,则∠ACO就是侧棱AC与底面BCD所成的角,计算得tan∠ACO = √2.
2. (多选)[贵州凯里一中2023高二月考]在正方体ABCD - A₁B₁C₁D₁中,下列说法正确的是 ( )
A. $BC_{1}\perp DA_{1}$
B. $BC_{1}\perp CA_{1}$
C. $BC_{1}$与平面$AA_{1}C_{1}C$所成的角为$\frac{\pi}{4}$
D. $BC_{1}$与平面ABCD所成的角为$\frac{\pi}{4}$
A. $BC_{1}\perp DA_{1}$
B. $BC_{1}\perp CA_{1}$
C. $BC_{1}$与平面$AA_{1}C_{1}C$所成的角为$\frac{\pi}{4}$
D. $BC_{1}$与平面ABCD所成的角为$\frac{\pi}{4}$
答案:
ABD 【解析】对A选项,连接B₁C,如图①,
∵A₁B₁//C₁D₁,A₁B₁ = C₁D₁,C₁D₁//CD,C₁D₁ = CD,
∴A₁B₁//CD,A₁B₁ = CD,
∴四边形A₁B₁CD为平行四边形,
∴A₁D//B₁C.
∵B₁C⊥BC₁,
∴BC₁⊥DA₁,故A正确.

对B选项,由题可得CD⊥平面BCC₁B₁,
∴CD⊥BC₁. 又CD∩A₁D = D,CD,A₁D⊂平面A₁B₁CD,
∴BC₁⊥平面A₁B₁CD,又CA₁⊂平面A₁B₁CD,
∴BC₁⊥CA₁,故B正确.
对C选项,连接BD,交AC于点O,连接C₁O,如图②.
∵A₁A⊥底面ABCD,BO⊂平面ABCD,
∴A₁A⊥BO.
∵BO⊥AC,A₁A∩AC = A,A₁A,AC⊂平面AA₁C₁C,
∴BO⊥平面AA₁C₁C.
∴BC₁与平面AA₁C₁C所成的角为∠BC₁O. 设正方体的棱长为1,则BO = √2 / 2,BC₁ = √2,
∴sin∠BC₁O = BO / BC₁ = (√2 / 2) / √2 = 1 / 2.
∵∠BC₁O∈(0, π / 2),
∴∠BC₁O = π / 6,故C错误.
对D选项,
∵C₁C⊥底面ABCD,
∴BC₁与平面ABCD所成的角为∠C₁BC. 易知△BCC₁为等腰直角三角形,
∴∠C₁BC = π / 4,故D正确. 故选ABD.

ABD 【解析】对A选项,连接B₁C,如图①,
∵A₁B₁//C₁D₁,A₁B₁ = C₁D₁,C₁D₁//CD,C₁D₁ = CD,
∴A₁B₁//CD,A₁B₁ = CD,
∴四边形A₁B₁CD为平行四边形,
∴A₁D//B₁C.
∵B₁C⊥BC₁,
∴BC₁⊥DA₁,故A正确.

对B选项,由题可得CD⊥平面BCC₁B₁,
∴CD⊥BC₁. 又CD∩A₁D = D,CD,A₁D⊂平面A₁B₁CD,
∴BC₁⊥平面A₁B₁CD,又CA₁⊂平面A₁B₁CD,
∴BC₁⊥CA₁,故B正确.
对C选项,连接BD,交AC于点O,连接C₁O,如图②.
∵A₁A⊥底面ABCD,BO⊂平面ABCD,
∴A₁A⊥BO.
∵BO⊥AC,A₁A∩AC = A,A₁A,AC⊂平面AA₁C₁C,
∴BO⊥平面AA₁C₁C.
∴BC₁与平面AA₁C₁C所成的角为∠BC₁O. 设正方体的棱长为1,则BO = √2 / 2,BC₁ = √2,
∴sin∠BC₁O = BO / BC₁ = (√2 / 2) / √2 = 1 / 2.
∵∠BC₁O∈(0, π / 2),
∴∠BC₁O = π / 6,故C错误.
对D选项,
∵C₁C⊥底面ABCD,
∴BC₁与平面ABCD所成的角为∠C₁BC. 易知△BCC₁为等腰直角三角形,
∴∠C₁BC = π / 4,故D正确. 故选ABD.

3. 直线l与平面$\alpha$所成的角是45°,若直线l在$\alpha$内的射影与$\alpha$内的直线m所成的角是45°,则l与m所成的角是 ( )
A. 30°
B. 45°
C. 60°
D. 90°
A. 30°
B. 45°
C. 60°
D. 90°
答案:
C 【解析】由题意,θ₁ = 45°,θ₂ = 45°. 由cosθ = cosθ₁·cosθ₂,得cosθ = 1 / 2,
∴θ = 60°. 故选C.
∴θ = 60°. 故选C.
4. [辽宁省实验中学2024高二期中]已知PA,PB,PC是从点P出发的三条射线,每两条射线的夹角均为60°,那么直线PC与平面PAB所成角的余弦值是 ( )
A. $\frac{\sqrt{6}}{3}$
B. $\frac{\sqrt{3}}{3}$
C. $\frac{\sqrt{2}}{2}$
D. $\frac{1}{2}$
A. $\frac{\sqrt{6}}{3}$
B. $\frac{\sqrt{3}}{3}$
C. $\frac{\sqrt{2}}{2}$
D. $\frac{1}{2}$
答案:
B 【解析】如图,设直线PC在平面PAB的射影为PD,
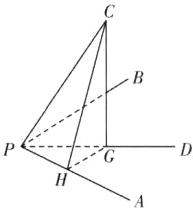
作CG⊥PD于点G,CH⊥PA于点H,连接HG,
易得CG⊥PA,又CH∩CG = C,CH,CG⊂平面CHG,则PA⊥平面CHG,又HG⊂平面CHG,则PA⊥HG,
则有
$\begin{cases}\cos\angle CPA=\frac{PH}{PC}, \\\cos\angle CPD\times\cos\angle APD=\frac{PG}{PC}\cdot\frac{PH}{PG}=\frac{PH}{PC},\end{cases}$
故cos∠CPA = cos∠CPD×cos∠APD.
已知∠APC = 60°,易得∠APD = 30°,
故cos∠CPD = cos∠CPA / cos∠APD = cos60° / cos30° = √3 / 3,又∠CPD即为直线PC与平面PAB所成的角,故所求角的余弦值为√3 / 3. 故选B.
【多种解法】如图所示,把PA,PB,PC放在正方体中,PA,PB,PC的夹角均为60°.

建立如图所示的空间直角坐标系,设正方体的棱长为1,
则P(1,0,0),C(0,0,1),A(1,1,1),B(0,1,0),
所以$\overrightarrow{PC}=(-1,0,1)$,$\overrightarrow{PA}=(0,1,1)$,$\overrightarrow{PB}=(-1,1,0)$,
设平面PAB的法向量为$\boldsymbol{n}=(x,y,z)$,则
$\begin{cases}\boldsymbol{n}\cdot\overrightarrow{PA}=y + z = 0, \\\boldsymbol{n}\cdot\overrightarrow{PB}=-x + y = 0,\end{cases}$
令x = 1,则y = 1,z = -1,所以$\boldsymbol{n}=(1,1,-1)$,
所以$\cos\langle\overrightarrow{PC},\boldsymbol{n}\rangle=\frac{\overrightarrow{PC}\cdot\boldsymbol{n}}{\vert\overrightarrow{PC}\vert\vert\boldsymbol{n}\vert}=\frac{-2}{\sqrt{2}\times\sqrt{3}}=-\frac{\sqrt{6}}{3}$.
设直线PC与平面PAB所成角为θ,
则sinθ = $\vert\cos\langle\overrightarrow{PC},\boldsymbol{n}\rangle\vert=\frac{\sqrt{6}}{3}$,
所以cosθ = $\sqrt{1 - \sin^{2}\theta}=\frac{\sqrt{3}}{3}$. 故选B.
B 【解析】如图,设直线PC在平面PAB的射影为PD,

作CG⊥PD于点G,CH⊥PA于点H,连接HG,
易得CG⊥PA,又CH∩CG = C,CH,CG⊂平面CHG,则PA⊥平面CHG,又HG⊂平面CHG,则PA⊥HG,
则有
$\begin{cases}\cos\angle CPA=\frac{PH}{PC}, \\\cos\angle CPD\times\cos\angle APD=\frac{PG}{PC}\cdot\frac{PH}{PG}=\frac{PH}{PC},\end{cases}$
故cos∠CPA = cos∠CPD×cos∠APD.
已知∠APC = 60°,易得∠APD = 30°,
故cos∠CPD = cos∠CPA / cos∠APD = cos60° / cos30° = √3 / 3,又∠CPD即为直线PC与平面PAB所成的角,故所求角的余弦值为√3 / 3. 故选B.
【多种解法】如图所示,把PA,PB,PC放在正方体中,PA,PB,PC的夹角均为60°.

建立如图所示的空间直角坐标系,设正方体的棱长为1,
则P(1,0,0),C(0,0,1),A(1,1,1),B(0,1,0),
所以$\overrightarrow{PC}=(-1,0,1)$,$\overrightarrow{PA}=(0,1,1)$,$\overrightarrow{PB}=(-1,1,0)$,
设平面PAB的法向量为$\boldsymbol{n}=(x,y,z)$,则
$\begin{cases}\boldsymbol{n}\cdot\overrightarrow{PA}=y + z = 0, \\\boldsymbol{n}\cdot\overrightarrow{PB}=-x + y = 0,\end{cases}$
令x = 1,则y = 1,z = -1,所以$\boldsymbol{n}=(1,1,-1)$,
所以$\cos\langle\overrightarrow{PC},\boldsymbol{n}\rangle=\frac{\overrightarrow{PC}\cdot\boldsymbol{n}}{\vert\overrightarrow{PC}\vert\vert\boldsymbol{n}\vert}=\frac{-2}{\sqrt{2}\times\sqrt{3}}=-\frac{\sqrt{6}}{3}$.
设直线PC与平面PAB所成角为θ,
则sinθ = $\vert\cos\langle\overrightarrow{PC},\boldsymbol{n}\rangle\vert=\frac{\sqrt{6}}{3}$,
所以cosθ = $\sqrt{1 - \sin^{2}\theta}=\frac{\sqrt{3}}{3}$. 故选B.
5. [河南商丘二中2024高二月考]在正方体ABCD - A₁B₁C₁D₁中,直线$BC_{1}$与平面$A_{1}BD$所成角的正弦值为 ( )
A. $\frac{\sqrt{2}}{2}$
B. $\frac{\sqrt{2}}{3}$
C. $\frac{\sqrt{3}}{2}$
D. $\frac{\sqrt{6}}{3}$
A. $\frac{\sqrt{2}}{2}$
B. $\frac{\sqrt{2}}{3}$
C. $\frac{\sqrt{3}}{2}$
D. $\frac{\sqrt{6}}{3}$
答案:
D 【解析】设正方体ABCD - A₁B₁C₁D₁的棱长为1,建立如图所示的空间直角坐标系,

则D(0,0,0),A₁(1,0,1),B(1,1,0),C₁(0,1,1),$\overrightarrow{BC_{1}}=(-1,0,1)$,$\overrightarrow{DA_{1}}=(1,0,1)$,$\overrightarrow{DB}=(1,1,0)$.
设平面A₁BD的法向量为$\boldsymbol{n}=(x,y,z)$,
则
$\begin{cases}\boldsymbol{n}\cdot\overrightarrow{DA_{1}}=x + z = 0, \\\boldsymbol{n}\cdot\overrightarrow{DB}=x + y = 0,\end{cases}$
得平面A₁BD的一个法向量为$\boldsymbol{n}=(1,-1,-1)$.
设直线BC₁与平面A₁BD所成的角为θ,
则sinθ = $\frac{\vert\boldsymbol{n}\cdot\overrightarrow{BC_{1}}\vert}{\vert\boldsymbol{n}\vert\vert\overrightarrow{BC_{1}}\vert}=\frac{2}{\sqrt{3}\times\sqrt{2}}=\frac{\sqrt{6}}{3}$. 故选D.
D 【解析】设正方体ABCD - A₁B₁C₁D₁的棱长为1,建立如图所示的空间直角坐标系,

则D(0,0,0),A₁(1,0,1),B(1,1,0),C₁(0,1,1),$\overrightarrow{BC_{1}}=(-1,0,1)$,$\overrightarrow{DA_{1}}=(1,0,1)$,$\overrightarrow{DB}=(1,1,0)$.
设平面A₁BD的法向量为$\boldsymbol{n}=(x,y,z)$,
则
$\begin{cases}\boldsymbol{n}\cdot\overrightarrow{DA_{1}}=x + z = 0, \\\boldsymbol{n}\cdot\overrightarrow{DB}=x + y = 0,\end{cases}$
得平面A₁BD的一个法向量为$\boldsymbol{n}=(1,-1,-1)$.
设直线BC₁与平面A₁BD所成的角为θ,
则sinθ = $\frac{\vert\boldsymbol{n}\cdot\overrightarrow{BC_{1}}\vert}{\vert\boldsymbol{n}\vert\vert\overrightarrow{BC_{1}}\vert}=\frac{2}{\sqrt{3}\times\sqrt{2}}=\frac{\sqrt{6}}{3}$. 故选D.
6. [山东聊城一中2024高二开学考试]在直三棱柱$ABC - A_{1}B_{1}C_{1}$中,$\triangle ABC$为等边三角形,$AA_{1}=AB$,M是$A_{1}C_{1}$的中点,则AM与平面$BCC_{1}B_{1}$所成角的正弦值为 ( )
A. $\frac{7}{10}$
B. $\frac{\sqrt{15}}{10}$
C. $\frac{\sqrt{85}}{10}$
D. $-\frac{\sqrt{15}}{10}$
A. $\frac{7}{10}$
B. $\frac{\sqrt{15}}{10}$
C. $\frac{\sqrt{85}}{10}$
D. $-\frac{\sqrt{15}}{10}$
答案:
B 【解析】如图所示,取AC的中点D,连接DM,BD,以D为原点,BD,DC,DM所在直线分别为x轴、y轴、z轴,建立空间直角坐标系.

不妨设AC = 2,则A(0,-1,0),C(0,1,0),M(0,0,2),B(-√3,0,0),所以$\overrightarrow{AM}=(0,1,2)$,$\overrightarrow{CC_{1}}=\overrightarrow{DM}=(0,0,2)$,$\overrightarrow{BC}=(\sqrt{3},1,0)$. 设平面BCC₁B₁的法向量为$\boldsymbol{n}=(x,y,z)$,则
$\begin{cases}\boldsymbol{n}\cdot\overrightarrow{CC_{1}}=0, \\\boldsymbol{n}\cdot\overrightarrow{BC}=0,\end{cases}$
即
$\begin{cases}2z = 0, \\\sqrt{3}x + y = 0,\end{cases}$
取x = √3 / 2,则y = -3 / 2,z = 0,所以$\boldsymbol{n}=(\frac{\sqrt{3}}{2},-\frac{3}{2},0)$.
设AM与平面BCC₁B₁所成角为α,向量$\overrightarrow{AM}$与$\boldsymbol{n}$所成的角为θ,所以sinα = $\vert\cos\theta\vert=\frac{\vert\overrightarrow{AM}\cdot\boldsymbol{n}\vert}{\vert\overrightarrow{AM}\vert\vert\boldsymbol{n}\vert}=\frac{\frac{3}{2}}{\sqrt{5}\times\sqrt{3}}=\frac{\sqrt{15}}{10}$,即AM与平面BCC₁B₁所成角的正弦值为√15 / 10. 故选B.
【归纳总结】求直线与平面所成角的方法
(1)定义法:①作,在直线上选取恰当的点向平面引垂线,确定垂足的位置是关键;
②证,证明所作的角为直线与平面所成的角,证明的主要依据是直线与平面所成角的概念;
③求,利用解三角形的知识求角.
(2)向量法:sinθ = $\vert\cos\langle\overrightarrow{AB},\boldsymbol{n}\rangle\vert=\frac{\vert\overrightarrow{AB}\cdot\boldsymbol{n}\vert}{\vert\overrightarrow{AB}\vert\vert\boldsymbol{n}\vert}$(其中$\overrightarrow{AB}$为直线AB的方向向量,$\boldsymbol{n}$为平面α的法向量,θ为直线AB与平面α所成的角),进一步,可根据θ∈[0, π / 2]确定角θ的大小.
B 【解析】如图所示,取AC的中点D,连接DM,BD,以D为原点,BD,DC,DM所在直线分别为x轴、y轴、z轴,建立空间直角坐标系.

不妨设AC = 2,则A(0,-1,0),C(0,1,0),M(0,0,2),B(-√3,0,0),所以$\overrightarrow{AM}=(0,1,2)$,$\overrightarrow{CC_{1}}=\overrightarrow{DM}=(0,0,2)$,$\overrightarrow{BC}=(\sqrt{3},1,0)$. 设平面BCC₁B₁的法向量为$\boldsymbol{n}=(x,y,z)$,则
$\begin{cases}\boldsymbol{n}\cdot\overrightarrow{CC_{1}}=0, \\\boldsymbol{n}\cdot\overrightarrow{BC}=0,\end{cases}$
即
$\begin{cases}2z = 0, \\\sqrt{3}x + y = 0,\end{cases}$
取x = √3 / 2,则y = -3 / 2,z = 0,所以$\boldsymbol{n}=(\frac{\sqrt{3}}{2},-\frac{3}{2},0)$.
设AM与平面BCC₁B₁所成角为α,向量$\overrightarrow{AM}$与$\boldsymbol{n}$所成的角为θ,所以sinα = $\vert\cos\theta\vert=\frac{\vert\overrightarrow{AM}\cdot\boldsymbol{n}\vert}{\vert\overrightarrow{AM}\vert\vert\boldsymbol{n}\vert}=\frac{\frac{3}{2}}{\sqrt{5}\times\sqrt{3}}=\frac{\sqrt{15}}{10}$,即AM与平面BCC₁B₁所成角的正弦值为√15 / 10. 故选B.
【归纳总结】求直线与平面所成角的方法
(1)定义法:①作,在直线上选取恰当的点向平面引垂线,确定垂足的位置是关键;
②证,证明所作的角为直线与平面所成的角,证明的主要依据是直线与平面所成角的概念;
③求,利用解三角形的知识求角.
(2)向量法:sinθ = $\vert\cos\langle\overrightarrow{AB},\boldsymbol{n}\rangle\vert=\frac{\vert\overrightarrow{AB}\cdot\boldsymbol{n}\vert}{\vert\overrightarrow{AB}\vert\vert\boldsymbol{n}\vert}$(其中$\overrightarrow{AB}$为直线AB的方向向量,$\boldsymbol{n}$为平面α的法向量,θ为直线AB与平面α所成的角),进一步,可根据θ∈[0, π / 2]确定角θ的大小.
7. [山东济宁2024高二期中]如图,在正四棱锥S - ABCD中,O为顶点S在底面ABCD内的射影,P为侧棱SD的中点,且$SO = OC$,则直线CD与平面PAC的夹角是 ( )
A. 45° B. 90° C. 30° D. 60°

A. 45° B. 90° C. 30° D. 60°

答案:
C 【解析】如图,以O为坐标原点,OB所在直线为x轴,OC所在直线为y轴,OS所在直线为z轴,建立空间坐标系Oxyz.

设OD = SO = OA = OB = OC = a,
则A(0,-a,0),C(0,a,0),D(-a,0,0),S(0,0,a),P(-a / 2,0,a / 2),
则$\overrightarrow{CA}=(0,-2a,0)$,$\overrightarrow{AP}=(-\frac{a}{2},a,\frac{a}{2})$,$\overrightarrow{CD}=(-a,-a,0)$.
设平面PAC的法向量为$\boldsymbol{n}=(x,y,z)$,
则$\boldsymbol{n}\cdot\overrightarrow{CA}=0$,$\boldsymbol{n}\cdot\overrightarrow{AP}=0$,
∴
$\begin{cases}-2ay = 0, \\-\frac{a}{2}x + ay+\frac{a}{2}z = 0,\end{cases}$
可取$\boldsymbol{n}=(1,0,1)$.
设直线CD与平面PAC的夹角为θ,
则sinθ = $\vert\cos\langle\overrightarrow{CD},\boldsymbol{n}\rangle\vert=\frac{\vert\overrightarrow{CD}\cdot\boldsymbol{n}\vert}{\vert\overrightarrow{CD}\vert\vert\boldsymbol{n}\vert}=\frac{\vert - a\vert}{\sqrt{2a^{2}}\times\sqrt{2}}=\frac{1}{2}$,又0°≤θ≤90°,
∴θ = 30°. 故选C.
C 【解析】如图,以O为坐标原点,OB所在直线为x轴,OC所在直线为y轴,OS所在直线为z轴,建立空间坐标系Oxyz.

设OD = SO = OA = OB = OC = a,
则A(0,-a,0),C(0,a,0),D(-a,0,0),S(0,0,a),P(-a / 2,0,a / 2),
则$\overrightarrow{CA}=(0,-2a,0)$,$\overrightarrow{AP}=(-\frac{a}{2},a,\frac{a}{2})$,$\overrightarrow{CD}=(-a,-a,0)$.
设平面PAC的法向量为$\boldsymbol{n}=(x,y,z)$,
则$\boldsymbol{n}\cdot\overrightarrow{CA}=0$,$\boldsymbol{n}\cdot\overrightarrow{AP}=0$,
∴
$\begin{cases}-2ay = 0, \\-\frac{a}{2}x + ay+\frac{a}{2}z = 0,\end{cases}$
可取$\boldsymbol{n}=(1,0,1)$.
设直线CD与平面PAC的夹角为θ,
则sinθ = $\vert\cos\langle\overrightarrow{CD},\boldsymbol{n}\rangle\vert=\frac{\vert\overrightarrow{CD}\cdot\boldsymbol{n}\vert}{\vert\overrightarrow{CD}\vert\vert\boldsymbol{n}\vert}=\frac{\vert - a\vert}{\sqrt{2a^{2}}\times\sqrt{2}}=\frac{1}{2}$,又0°≤θ≤90°,
∴θ = 30°. 故选C.
8. [浙江杭师大附中2024高二期中]如图,在三棱锥S - ABC中,$SC\perp$平面ABC,点P,M分别是SC和SB的中点,$PM = AC = 1$,$\angle ACB = 90^{\circ}$,直线AM与直线SC所成的角为60°.
(1)求SC的长;
(2)求直线CM与平面AMP所成角的正弦值.

(1)求SC的长;
(2)求直线CM与平面AMP所成角的正弦值.

答案:
【解】
(1)由SC⊥平面ABC,且∠ACB = 90°,可得AC,BC,SC两两垂直,
如图,以C为坐标原点,AC,BC,SC所在直线分别为x,y,z轴建立空间直角坐标系.

设SC = 2a(a>0),则A(1,0,0),B(0,2,0),C(0,0,0),S(0,0,2a),M(0,1,a),P(0,0,a),
可得$\overrightarrow{AM}=(-1,1,a)$,$\overrightarrow{CS}=(0,0,2a)$,
所以$\vert\cos\langle\overrightarrow{AM},\overrightarrow{CS}\rangle\vert=\frac{\vert\overrightarrow{AM}\cdot\overrightarrow{CS}\vert}{\vert\overrightarrow{AM}\vert\vert\overrightarrow{CS}\vert}=\frac{2a^{2}}{\sqrt{2 + a^{2}}\times2a}=\frac{1}{2}$,解得a = √6 / 3,
所以SC = 2a = 2√6 / 3.
(2)由
(1)可得$\overrightarrow{AP}=(-1,0,\frac{\sqrt{6}}{3})$,$\overrightarrow{PM}=(0,1,0)$,$\overrightarrow{CM}=(0,1,\frac{\sqrt{6}}{3})$,
设平面AMP的法向量为$\boldsymbol{n}=(x,y,z)$,则
$\begin{cases}\boldsymbol{n}\cdot\overrightarrow{AP}=-x+\frac{\sqrt{6}}{3}z = 0, \\\boldsymbol{n}\cdot\overrightarrow{PM}=y = 0,\end{cases}$
令x = √2,则y = 0,z = √3,
可得$\boldsymbol{n}=(\sqrt{2},0,\sqrt{3})$,
则$\cos\langle\boldsymbol{n},\overrightarrow{CM}\rangle=\frac{\boldsymbol{n}\cdot\overrightarrow{CM}}{\vert\boldsymbol{n}\vert\vert\overrightarrow{CM}\vert}=\frac{\sqrt{2}}{\sqrt{5}\times\frac{\sqrt{5}}{\sqrt{3}}}=\frac{\sqrt{6}}{5}$,所以直线CM与平面AMP所成角的正弦值为√6 / 5.
【归纳总结】求空间角的常用方法
(1)定义法:由异面直线所成角、线面角、二面角的定义,结合图形,作出所求空间角,再结合题中条件,解对应三角形,即可求出结果;
(2)向量法:建立适当的空间直角坐标系,通过计算向量夹角(直线方向向量与直线方向向量、直线方向向量与平面法向量、平面法向量与平面法向量)的余弦值,再进行转化求出结果.
【解】
(1)由SC⊥平面ABC,且∠ACB = 90°,可得AC,BC,SC两两垂直,
如图,以C为坐标原点,AC,BC,SC所在直线分别为x,y,z轴建立空间直角坐标系.

设SC = 2a(a>0),则A(1,0,0),B(0,2,0),C(0,0,0),S(0,0,2a),M(0,1,a),P(0,0,a),
可得$\overrightarrow{AM}=(-1,1,a)$,$\overrightarrow{CS}=(0,0,2a)$,
所以$\vert\cos\langle\overrightarrow{AM},\overrightarrow{CS}\rangle\vert=\frac{\vert\overrightarrow{AM}\cdot\overrightarrow{CS}\vert}{\vert\overrightarrow{AM}\vert\vert\overrightarrow{CS}\vert}=\frac{2a^{2}}{\sqrt{2 + a^{2}}\times2a}=\frac{1}{2}$,解得a = √6 / 3,
所以SC = 2a = 2√6 / 3.
(2)由
(1)可得$\overrightarrow{AP}=(-1,0,\frac{\sqrt{6}}{3})$,$\overrightarrow{PM}=(0,1,0)$,$\overrightarrow{CM}=(0,1,\frac{\sqrt{6}}{3})$,
设平面AMP的法向量为$\boldsymbol{n}=(x,y,z)$,则
$\begin{cases}\boldsymbol{n}\cdot\overrightarrow{AP}=-x+\frac{\sqrt{6}}{3}z = 0, \\\boldsymbol{n}\cdot\overrightarrow{PM}=y = 0,\end{cases}$
令x = √2,则y = 0,z = √3,
可得$\boldsymbol{n}=(\sqrt{2},0,\sqrt{3})$,
则$\cos\langle\boldsymbol{n},\overrightarrow{CM}\rangle=\frac{\boldsymbol{n}\cdot\overrightarrow{CM}}{\vert\boldsymbol{n}\vert\vert\overrightarrow{CM}\vert}=\frac{\sqrt{2}}{\sqrt{5}\times\frac{\sqrt{5}}{\sqrt{3}}}=\frac{\sqrt{6}}{5}$,所以直线CM与平面AMP所成角的正弦值为√6 / 5.
【归纳总结】求空间角的常用方法
(1)定义法:由异面直线所成角、线面角、二面角的定义,结合图形,作出所求空间角,再结合题中条件,解对应三角形,即可求出结果;
(2)向量法:建立适当的空间直角坐标系,通过计算向量夹角(直线方向向量与直线方向向量、直线方向向量与平面法向量、平面法向量与平面法向量)的余弦值,再进行转化求出结果.
9. 已知向量$\boldsymbol{m}$,$\boldsymbol{n}$分别是直线l的方向向量和平面$\alpha$的法向量. 若$\cos\langle\boldsymbol{m},\boldsymbol{n}\rangle=-\frac{\sqrt{3}}{2}$,则l与$\alpha$所成角的大小为________.
答案:
60° 【解析】设l与α所成角为θ,则sinθ = $\vert\cos\langle\boldsymbol{m},\boldsymbol{n}\rangle\vert=\frac{\sqrt{3}}{2}$,
∴θ = 60°.
∴θ = 60°.
10. 平面$\alpha$的斜线l与它在这个平面上的射影$l'$的方向向量分别为$\boldsymbol{a}=(1,0,1)$,$\boldsymbol{b}=(0,1,1)$,则斜线l与平面$\alpha$所成角的大小为________.
答案:
60° 【解析】由线面角的含义知,$\langle\boldsymbol{a},\boldsymbol{b}\rangle$即为线面所成角或其补角.
∵$\cos\langle\boldsymbol{a},\boldsymbol{b}\rangle=\frac{\boldsymbol{a}\cdot\boldsymbol{b}}{\vert\boldsymbol{a}\vert\vert\boldsymbol{b}\vert}=\frac{(1,0,1)\cdot(0,1,1)}{\sqrt{1^{2}+1^{2}}\times\sqrt{1^{2}+1^{2}}}=\frac{1}{2}$,
∴$\langle\boldsymbol{a},\boldsymbol{b}\rangle = 60°$. 故斜线l与平面α所成角的大小为60°.
【易错警示】易忽略向量夹角和直线与平面所成角之间的非等量关系. 若直线的方向向量为$\boldsymbol{v}$,平面法向量为$\boldsymbol{n}$,直线与平面所成角为θ,则sinθ = $\vert\cos\langle\boldsymbol{v},\boldsymbol{n}\rangle\vert$,当$\langle\boldsymbol{v},\boldsymbol{n}\rangle\in(0,\frac{\pi}{2})$时,θ = $\frac{\pi}{2}-\langle\boldsymbol{v},\boldsymbol{n}\rangle$;当$\langle\boldsymbol{v},\boldsymbol{n}\rangle\in(\frac{\pi}{2},\pi)$时,θ = $\langle\boldsymbol{v},\boldsymbol{n}\rangle-\frac{\pi}{2}$.
∵$\cos\langle\boldsymbol{a},\boldsymbol{b}\rangle=\frac{\boldsymbol{a}\cdot\boldsymbol{b}}{\vert\boldsymbol{a}\vert\vert\boldsymbol{b}\vert}=\frac{(1,0,1)\cdot(0,1,1)}{\sqrt{1^{2}+1^{2}}\times\sqrt{1^{2}+1^{2}}}=\frac{1}{2}$,
∴$\langle\boldsymbol{a},\boldsymbol{b}\rangle = 60°$. 故斜线l与平面α所成角的大小为60°.
【易错警示】易忽略向量夹角和直线与平面所成角之间的非等量关系. 若直线的方向向量为$\boldsymbol{v}$,平面法向量为$\boldsymbol{n}$,直线与平面所成角为θ,则sinθ = $\vert\cos\langle\boldsymbol{v},\boldsymbol{n}\rangle\vert$,当$\langle\boldsymbol{v},\boldsymbol{n}\rangle\in(0,\frac{\pi}{2})$时,θ = $\frac{\pi}{2}-\langle\boldsymbol{v},\boldsymbol{n}\rangle$;当$\langle\boldsymbol{v},\boldsymbol{n}\rangle\in(\frac{\pi}{2},\pi)$时,θ = $\langle\boldsymbol{v},\boldsymbol{n}\rangle-\frac{\pi}{2}$.
查看更多完整答案,请扫码查看


