《2024年高中必刷题高二数学选择性必修第一册人教B版》

1. 在空间直角坐标系Oxyz中，已知两点P₁(1,1,0)，P₂(-2,1,3)，则这两点间的距离为（ ）
A. √21
B. $\sqrt{22}$
C. 3√2
D. 18

答案： 1. C 【解析】已知在空间直角坐标系中，$P_1(1,1,0)$，$P_2(-2,1,3)$，则这两点间的距离$|P_1P_2|=\sqrt{(1 + 2)^2+(1 - 1)^2+(0 - 3)^2}=3\sqrt{2}$。故选 C。

2. 如图所示，在平行四边形AB -CD中，AB = AC = 1，∠ACD = 90°，将它沿对角线AC折起，使直线AB与CD成60°角，则B，D间的距离等于（ ）

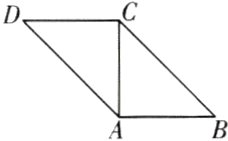
A. √2
B. 1
C. $\sqrt{2}$或2
D. 1或√2

答案：
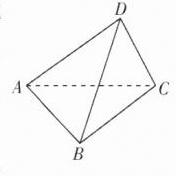
2. C 【解析】$\because\angle ACD = 90^{\circ}$，$\therefore\overrightarrow{AC}\cdot\overrightarrow{CD}=0$，同理，$\overrightarrow{AC}\cdot\overrightarrow{BA}=0$。又$\because AB$与$CD$成$60^{\circ}$角，$\therefore\langle\overrightarrow{BA},\overrightarrow{CD}\rangle = 60^{\circ}$或$\langle\overrightarrow{BA},\overrightarrow{CD}\rangle = 120^{\circ}$。
$\because\overrightarrow{BD}=\overrightarrow{BA}+\overrightarrow{AC}+\overrightarrow{CD}$，$\therefore\overrightarrow{BD}^2=|\overrightarrow{BA}|^2+|\overrightarrow{AC}|^2+|\overrightarrow{CD}|^2+2\overrightarrow{BA}\cdot\overrightarrow{AC}+2\overrightarrow{BA}\cdot\overrightarrow{CD}+2\overrightarrow{AC}\cdot\overrightarrow{CD}=3 + 2\times1\times1\times\cos\langle\overrightarrow{BA},\overrightarrow{CD}\rangle=3\pm1$，$\therefore\overrightarrow{BD}^2 = 4$或$\overrightarrow{BD}^2 = 2$，$\therefore|\overrightarrow{BD}| = 2$或$|\overrightarrow{BD}|=\sqrt{2}$，故选 C。

3. [辽宁沈阳实验中学2023高二开学考试]正四棱柱ABCD - A₁B₁C₁D₁中，底面边长为1，侧棱长为2，P，Q分别是异面直线AD₁和BD上的任意一点，则P，Q间距离的最小值为________.

答案：
3. $\frac{2}{3}$ 【解析】建立如图所示的空间直角坐标系，则$D_1(0,0,0)$，$A(1,0,2)$，$D(0,0,2)$，$B(1,1,2)$，所以$\overrightarrow{D_1A}=(1,0,2)$，$\overrightarrow{DB}=(1,1,0)$，$\overrightarrow{DA}=(1,0,0)$。

设$\boldsymbol{n}=(x,y,z)$且$\begin{cases}\boldsymbol{n}\cdot\overrightarrow{D_1A}=0\\\boldsymbol{n}\cdot\overrightarrow{DB}=0\end{cases}$，即$\begin{cases}x + 2z = 0\\x + y = 0\end{cases}$，令$z = 1$，则$x = - 2$，$y = 2$，所以$\boldsymbol{n}=(-2,2,1)$，所以异面直线$AD_1$和$BD$的距离$d=\frac{|\boldsymbol{n}\cdot\overrightarrow{DA}|}{|\boldsymbol{n}|}=\frac{2}{3}$，所以$P$，$Q$间距离的最小值为$\frac{2}{3}$。
【规律方法】求异面直线距离的方法：先求两异面直线的公共法向量，再求两异面直线上任意两点的连接线段在公共法向量上的射影长。公共法向量$\boldsymbol{n}$可以利用向量数量积找到，设两异面直线上任意两点所连成的向量为$\boldsymbol{m}$，且$\boldsymbol{m}$，$\boldsymbol{n}$的夹角为$\theta$，则异面直线的距离$d = |\boldsymbol{m}||\cos\theta|=|\boldsymbol{m}|\cdot\frac{|\boldsymbol{m}\cdot\boldsymbol{n}|}{|\boldsymbol{m}||\boldsymbol{n}|}=\frac{|\boldsymbol{m}\cdot\boldsymbol{n}|}{|\boldsymbol{n}|}$。该公式可以这样理解：设异面直线$AM$和$BN$，其中$AB$是公垂线，$M$，$N$是两条直线上任意的两点。明显地，$MA\perp AB$，$NB\perp AB$，根据射影的定义可知，$\overrightarrow{AB}$是$\overrightarrow{MN}$的射影，而$|\overrightarrow{AB}|$就是异面直线的距离。

4. [山东临沂2024高二学科素养水平监测]已知过坐标原点O的直线l的方向向量u=(1,1,1)，则点P(1,2,3)到直线l的距离是（ ）
A. 2
B. √5
C. √3
D. $\sqrt{2}$

答案： 4. D 【解析】由题意可知，$\overrightarrow{OP}$在直线$l$上的投影向量的模长为$\left|\frac{\overrightarrow{OP}\cdot\boldsymbol{u}}{|\boldsymbol{u}|}\right|=\frac{6}{\sqrt{3}}=2\sqrt{3}$，所以点$P(1,2,3)$到直线$l$的距离$d=\sqrt{|\overrightarrow{OP}|^2-\left|\frac{\overrightarrow{OP}\cdot\boldsymbol{u}}{|\boldsymbol{u}|}\right|^2}=\sqrt{2}$。故点$P(1,2,3)$到直线$l$的距离是$\sqrt{2}$。故选 D。

5. [山西太原2024高二期中学业诊断]如图，正方体ABCD -

A₁B₁C₁D₁的棱长为2，E是CC₁的中点，则点A到直线D₁E的距离为（ ）
A. $\frac{\sqrt{2}}{2}$
B. $\frac{\sqrt{30}}{2}$
C. $\frac{2\sqrt{5}}{5}$
D. $\frac{6\sqrt{5}}{5}$

答案：
5. D 【解析】建立如图所示的空间直角坐标系，连接$AD_1$，则$D_1(0,0,2)$，$E(0,2,1)$，$A(2,0,0)$，

所以$\overrightarrow{D_1E}=(0,2,-1)$，$\overrightarrow{D_1A}=(2,0,-2)$，所以点$A$到直线$D_1E$的距离为$\sqrt{|\overrightarrow{D_1A}|^2-\left(\frac{\overrightarrow{D_1E}\cdot\overrightarrow{D_1A}}{|\overrightarrow{D_1E}|}\right)^2}=\sqrt{8 - \left(\frac{2}{\sqrt{5}}\right)^2}=\frac{6\sqrt{5}}{5}$。故选 D。

6. [浙江台州2024高二期中]在空间直角坐标系Oxyz中，已知点A(1,2,0)，B(0,1,2)，C(1,0,2)，则点O到平面ABC的距离是（ ）
A. $\sqrt{2}$
B. $\sqrt{3}$
C. $\sqrt{5}$
D. 2√2

答案： 6. B 【解析】依题意可得$\overrightarrow{AB}=(-1,-1,2)$，$\overrightarrow{BC}=(1,-1,0)$，$\overrightarrow{OA}=(1,2,0)$，设平面$ABC$的法向量为$\boldsymbol{n}=(x,y,z)$，则$\begin{cases}\boldsymbol{n}\cdot\overrightarrow{AB}=-x - y + 2z = 0\\\boldsymbol{n}\cdot\overrightarrow{BC}=x - y = 0\end{cases}$，令$x = 1$，则可得$y = 1$，$z = 1$，即$\boldsymbol{n}=(1,1,1)$，所以点$O$到平面$ABC$的距离$d=\frac{|\overrightarrow{OA}\cdot\boldsymbol{n}|}{|\boldsymbol{n}|}=\frac{1 + 2}{\sqrt{3}}=\sqrt{3}$。故选 B。

7. [广东惠州实验中学2024高二月考]在四棱锥P - ABCD中，$\overrightarrow{PA}=(-1,2,2)$，$\overrightarrow{AB}=(1,2,-3)$，$\overrightarrow{AC}=(0,-1,2)$，则该四棱锥的高为（ ）
A. $\frac{\sqrt{30}}{2}$
B. $\frac{7\sqrt{6}}{2}$
C. $\frac{\sqrt{30}}{6}$
D. $\frac{7\sqrt{6}}{6}$

答案： 7. D 【解析】设平面$ABCD$的法向量为$\boldsymbol{n}=(x,y,z)$，则$\begin{cases}\boldsymbol{n}\cdot\overrightarrow{AB}=0\\\boldsymbol{n}\cdot\overrightarrow{AC}=0\end{cases}$，即$\begin{cases}x + 2y - 3z = 0\\-y + 2z = 0\end{cases}$，令$y = 2$，可得$x = - 1$，$z = 1$，则$\boldsymbol{n}=(-1,2,1)$。$\therefore$点$P$到平面$ABCD$的距离为$\frac{|\overrightarrow{PA}\cdot\boldsymbol{n}|}{|\boldsymbol{n}|}=\frac{7}{\sqrt{6}}=\frac{7\sqrt{6}}{6}$，即为该四棱锥的高。故选 D。

8. 已知平面α的一个法向量n = (-2,-2,1)，点A(-1,3,0)在平面α内，若点P(-2,1,z)到α的距离为$\frac{10}{3}$，则z = （ ）
A. 16
B. -4
C. 4或 - 16
D. -4或16

答案： 8. C 【解析】由点$A(-1,3,0)$在平面$\alpha$内，点$P(-2,1,z)$，可得$\overrightarrow{AP}=(-1,-2,z)$。因为平面$\alpha$的一个法向量$\boldsymbol{n}=(-2,-2,1)$，且点$P(-2,1,z)$到$\alpha$的距离为$\frac{10}{3}$，所以$\frac{|\overrightarrow{AP}\cdot\boldsymbol{n}|}{|\boldsymbol{n}|}=\frac{10}{3}$，即$\frac{|2 + 4+z|}{\sqrt{4 + 4 + 1}}=\frac{10}{3}$，解得$z = 4$或$z = - 16$。故选 C。

9. [广东佛山顺德区2023高二期中]如图，在长方体ABCD - A₁B₁C₁D₁中，AD = AA₁ = 1，AB = 2，求：
(1)点A₁到直线BD的距离；
(2)点A₁到平面BDC₁的距离；
(3)异面直线BD，CD₁之间的距离.

答案：
9.【解】
(1)以点$D$为坐标原点，$\overrightarrow{DA}$，$\overrightarrow{DC}$，$\overrightarrow{DD_1}$的方向分别为$x$，$y$，$z$轴的正方向建立空间直角坐标系。因为$AD = AA_1 = 1$，$AB = 2$，则$D(0,0,0)$，$B(1,2,0)$，$A_1(1,0,1)$，$C_1(0,2,1)$，$C(0,2,0)$，$D_1(0,0,1)$，所以$\overrightarrow{BD}=(-1,-2,0)$，$\overrightarrow{A_1B}=(0,2,-1)$，所以$\overrightarrow{A_1B}$在$\overrightarrow{BD}$上的投影向量的模为$\frac{|\overrightarrow{A_1B}\cdot\overrightarrow{BD}|}{|\overrightarrow{BD}|}=\frac{|-1\times0+(-2)\times2+0\times(-1)|}{\sqrt{(-1)^2+(-2)^2+0^2}}=\frac{4\sqrt{5}}{5}$，又$|\overrightarrow{A_1B}|=\sqrt{0^2+2^2+(-1)^2}=\sqrt{5}$，所以点$A_1$到直线$BD$的距离$d_1=\sqrt{5-\frac{16}{5}}=\frac{3\sqrt{5}}{5}$。

(2)由
(1)知$\overrightarrow{BD}=(-1,-2,0)$，$\overrightarrow{DC_1}=(0,2,1)$，$\overrightarrow{A_1B}=(0,2,-1)$。设平面$BDC_1$的法向量$\boldsymbol{n}=(x,y,z)$，则$\begin{cases}\boldsymbol{n}\cdot\overrightarrow{BD}=0\\\boldsymbol{n}\cdot\overrightarrow{DC_1}=0\end{cases}$，所以$\begin{cases}-x - 2y = 0\\2y + z = 0\end{cases}$，取$y = 1$，可得$x = - 2$，$z = - 2$，所以$\boldsymbol{n}=(-2,1,-2)$是平面$BDC_1$的一个法向量。向量$\overrightarrow{A_1B}=(0,2,-1)$在法向量$\boldsymbol{n}=(-2,1,-2)$上的投影向量的模为$\frac{|\overrightarrow{A_1B}\cdot\boldsymbol{n}|}{|\boldsymbol{n}|}=\frac{|-2\times0+1\times2+(-2)\times(-1)|}{\sqrt{(-2)^2+1^2+(-2)^2}}=\frac{4}{3}$，所以点$A_1$到平面$BDC_1$的距离为$\frac{4}{3}$。
(3)由
(1)知$\overrightarrow{CD_1}=(0,-2,1)$，$\overrightarrow{BA_1}=(0,-2,1)$，所以$\overrightarrow{CD_1}//\overrightarrow{BA_1}$。又$CD_1\not\subset$平面$A_1BD$，$BA_1\subset$平面$A_1BD$，所以$CD_1//$平面$A_1BD$，所以异面直线$BD$，$CD_1$之间的距离与点$C$到平面$A_1BD$的距离相等，设平面$A_1BD$的法向量$\boldsymbol{m}=(x_1,y_1,z_1)$，因为$\overrightarrow{BD}=(-1,-2,0)$，则$\begin{cases}\boldsymbol{m}\cdot\overrightarrow{BD}=0\\\boldsymbol{m}\cdot\overrightarrow{BA_1}=0\end{cases}$，所以$\begin{cases}-x_1 - 2y_1 = 0\\-2y_1+z_1 = 0\end{cases}$，取$y_1 = 1$，可得$x_1 = - 2$，$z_1 = 2$，所以$\boldsymbol{m}=(-2,1,2)$是平面$A_1BD$的一个法向量，向量$\overrightarrow{CD}=(0,-2,0)$在法向量$\boldsymbol{m}=(-2,1,2)$上的投影向量的模为$\frac{|\overrightarrow{CD}\cdot\boldsymbol{m}|}{|\boldsymbol{m}|}=\frac{|-2\times0+1\times(-2)+2\times0|}{\sqrt{(-2)^2+1^2+2^2}}=\frac{2}{3}$，所以点$C$到平面$A_1BD$的距离为$\frac{2}{3}$，故异面直线$BD$，$CD_1$之间的距离为$\frac{2}{3}$。