《2024年高中必刷题高二数学选择性必修第一册人教B版》

1. [陕西西安长安区一中2024高二期中]已知点P在椭圆C:$\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}} = 1(a＞b＞0)$上,点$F_{1},F_{2}$分别为椭圆C的左、右焦点,满足$PF_{1}\perp PF_{2}$,$\triangle PF_{1}F_{2}$的面积为12,椭圆C的焦距为8,则椭圆C的标准方程为 ( )
A. $\frac{x^{2}}{88}+\frac{y^{2}}{24}=1$
B. $\frac{x^{2}}{76}+\frac{y^{2}}{12}=1$
C. $\frac{x^{2}}{40}+\frac{y^{2}}{24}=1$
D. $\frac{x^{2}}{28}+\frac{y^{2}}{12}=1$

答案： D 【解析】由椭圆C的焦距为8，得|F₁F₂| = 2c = 8.
由PF₁⊥PF₂，△PF₁F₂的面积为12，
得$\frac{1}{2}$|PF₁||PF₂| = 12，
即|PF₁||PF₂| = 24.
因为|PF₁|² + |PF₂|² = |F₁F₂|² = 64，
所以（|PF₁| + |PF₂|）² = |PF₁|² + |PF₂|² + 2|PF₁||PF₂| = 112，即4a² = 112，a² = 28，
又c = 4，则b² = a² - c² = 12，则椭圆C的标准方程为$\frac{x^{2}}{28}$ + $\frac{y^{2}}{12}$ = 1. 故选D.

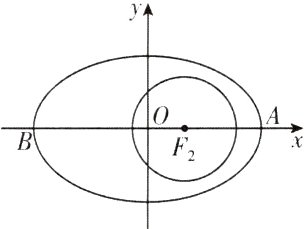
2. [湖北武汉部分重点中学2024高二期中联考]卫星的“地球同步转移轨道”是一个以地心(地球的中心)$F_{2}$为焦点的椭圆,如图,已知它的近地点(离地面最近的点)A距地面m(天文单位:A.U.),远地点(离地面最远的点)B距地面n(天文单位:A.U.),并且$F_{2},A,B$在同一直线上,地球半径约为r(天文单位:A.U.),则卫星轨道的离心率为 ( )

A. $\frac{m + n}{2r + m + n}$
B. $\frac{n - m}{2r + m + n}$
C. $\frac{n - m}{m + n}$
D. $\frac{n - m}{2r - m + n}$

答案：
B 【解析】设卫星轨道所在的椭圆的方程为$\frac{x^{2}}{a^{2}}$ + $\frac{y^{2}}{b^{2}}$ = 1（a＞b＞0）.
由题意得|AF₂| = m + r，|BF₂| = n + r，则卫星轨道的长轴长为|AB| = m + r + n + r = m + n + 2r，即2a = m + n + 2r.
设卫星轨道的左焦点为F₁，如图，由对称性可知，|BF₁| = |AF₂|，
则由椭圆定义可得2c = |BF₂| - |BF₁| = |BF₂| - |AF₂| = n + r - m - r = n - m，则卫星轨道的离心率为$\frac{c}{a}$ = $\frac{n - m}{m + n + 2r}$. 故选B.

3. [山东济宁一中2024高二质检]已知椭圆$\frac{x^{2}}{4}+\frac{y^{2}}{2}=1$上有一点P,$F_{1},F_{2}$是椭圆的左、右焦点.若$\triangle F_{1}PF_{2}$为直角三角形,则这样的点P有 ( )
A. 3个
B. 4个
C. 6个
D. 8个

答案： C 【解析】当∠PF₁F₂为直角时，根据椭圆的对称性知，这样的点P有2个；
同理当∠PF₂F₁为直角时，这样的点P有2个；
当点P为椭圆的短轴端点时，∠F₁PF₂最大，且为直角，此时这样的点P有2个.
故符合要求的点P有6个.

4. (多选)人造地球卫星绕地球运行遵循开普勒行星运动定律:卫星在以地球为右焦点的椭圆轨道上绕地球运行时,其运行速度是变化的,速度的变化服从面积守恒规律,即卫星的向径(卫星与地球的连线)在相同的时间内扫过的面积相等.设椭圆的长轴长、焦距分别为2a,2c,则下列结论正确的是 ( )
A. 卫星向径的取值范围是$[a - c,a + c]$
B. 卫星运行速度在远地点时最小,在近地点时最大
C. 卫星在左半椭圆弧轨道的运行时间小于其在右半椭圆弧轨道的运行时间
D. 卫星向径的最小值与最大值的比值越小,椭圆轨道越圆

答案： AB 【解析】A选项，由题意可得卫星的向径是椭圆上的点到右焦点的距离，所以最小值为a - c，最大值为a + c，即卫星向径的取值范围是[a - c，a + c]，故A正确；
B选项，因为运行速度是变化的，速度的变化服从卫星的向径（卫星与地球的连线）在相同的时间内扫过的面积相等，则向径越大，速度越小，所以卫星在近地点时向径最小，故速度最大，在远地点时向径最大，故速度最小，故B正确；
C选项，当卫星在左半椭圆弧轨道上运行时，对应的向径更大，根据面积守恒规律，速度更慢，所以卫星在左半椭圆弧轨道上的运行时间大于在右半椭圆弧轨道上的运行时间，故C不正确；
D选项，卫星向径的最小值与最大值的比值越小，即$\frac{a - c}{a + c}$ = $\frac{1 - e}{1 + e}$ = - 1 + $\frac{2}{1 + e}$越小，则e越大，椭圆轨道越扁，故D不正确. 故选AB.

5. [河南省实验中学2024高二期中]设B是椭圆C:$\frac{x^{2}}{a^{2}}+y^{2}=1(a＞1)$的上顶点,若椭圆C上的任意一点P都满足$|PB|\leq2$,则C的离心率的取值范围是 .

答案： $(0,\frac{\sqrt{2}}{2}]$ 【解析】设P(x₀，y₀)，由题得B(0，1)，|PB| ≤ 2，则x₀² + (y₀ - 1)² ≤ 4，即a²(1 - y₀²) + (y₀ - 1)² ≤ 4，故(a² - 1)y₀² + 2y₀ - a² + 3 ≥ 0，
即(y₀ + 1)[(a² - 1)y₀ - a² + 3] ≥ 0.
又y₀ ∈ [- 1，1]，所以(a² - 1)y₀ - a² + 3 ≥ 0对y₀ ∈ [- 1，1]恒成立，即(a² - 1)×(- 1) - a² + 3 ≥ 0，
解得a ∈ (1，$\sqrt{2}$]，则e² = $\frac{c^{2}}{a^{2}}$ = 1 - $\frac{1}{a^{2}}$ ∈ $(0,\frac{1}{2}]$，即e ∈ $(0,\frac{\sqrt{2}}{2}]$，故椭圆C的离心率的取值范围为$(0,\frac{\sqrt{2}}{2}]$.
【归纳总结】椭圆的离心率是椭圆最重要的几何性质，求椭圆的离心率（或离心率的取值范围），常见有两种方法：
①求出a，c，代入公式e = $\frac{c}{a}$；
②只需要根据条件得到关于a，b，c的齐次式，结合b² = a² - c²转化为关于a，c的齐次式，然后等式（不等式）两边同时除以a或a²转化为关于e的方程（不等式），解方程（不等式）即可得e（e的取值范围）.

6. [天津第一中学2023高二期中]如果实数x,y满足等式$3x^{2}+4y^{2}=12$,那么$\frac{y}{x - 3}$的最大值是 .

答案：
$\frac{\sqrt{15}}{5}$
【思路导引】化简等式3x² + 4y² = 12，可得到x，y满足椭圆方程$\frac{x^{2}}{4}$ + $\frac{y^{2}}{3}$ = 1，$\frac{y}{x - 3}$可看作点(3，0)与椭圆上的点连线的斜率，临界条件为相切，联立直线与椭圆的方程，由Δ = 0得到斜率的临界值，根据斜率的范围即可得$\frac{y}{x - 3}$的最大值.
【解析】由题知，3x² + 4y² = 12即$\frac{x^{2}}{4}$ + $\frac{y^{2}}{3}$ = 1，所以(x，y)是椭圆$\frac{x^{2}}{4}$ + $\frac{y^{2}}{3}$ = 1上点的坐标，记m = $\frac{y}{x - 3}$，即y = m(x - 3)，即m为点(3，0)与椭圆上的点连线的斜率，当直线y = m(x - 3)与椭圆相切时，斜率m可取得最值，如图所示.

联立直线和椭圆的方程，得$\begin{cases}3x^{2}+4y^{2}=12\\y = m(x - 3)\end{cases}$，整理可得(3 + 4m²)x² - 24m²x + 36m² - 12 = 0，因为直线与椭圆相切，所以Δ = (- 24m²)² - 4(3 + 4m²)·(36m² - 12) = 48(3 - 5m²) = 0，所以m² = $\frac{3}{5}$.
因此$\frac{y}{x - 3}$的取值范围为-$\frac{\sqrt{15}}{5}$ ≤ m ≤ $\frac{\sqrt{15}}{5}$，即$\frac{y}{x - 3}$的最大值是$\frac{\sqrt{15}}{5}$.

7. [浙江大学2023强基计划]过椭圆$\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1(a＞b＞0)$的右焦点作相互垂直的弦AC,BD.若四边形ABCD的面积的取值范围为$[8,\frac{25}{2}]$,则$\frac{a}{b}=$ .

答案：
2 【解析】设弦AC所在直线与x轴正方向的夹角为θ，则|AC| = $\frac{2ab^{2}}{a^{2}-c^{2}\cos^{2}\theta}$，|BD| = $\frac{2ab^{2}}{a^{2}-c^{2}\sin^{2}\theta}$，
∴ 四边形ABCD的面积S = $\frac{2a^{2}b^{4}}{a^{4}-a^{2}c^{2}+c^{4}\cos^{2}\theta\sin^{2}\theta}$ ≤ $\frac{2a^{2}b^{4}}{a^{4}-a^{2}c^{2}}$ = $\frac{2b^{4}}{b^{2}}$ = 2b² = $\frac{25}{2}$，
∴ b² = $\frac{25}{4}$；
S = $\frac{2a^{2}b^{4}}{a^{4}-a^{2}c^{2}+c^{4}\cos^{2}\theta\sin^{2}\theta}$ ≥ $\frac{2a^{2}b^{4}}{a^{4}-a^{2}c^{2}+\frac{1}{4}c^{4}}$ = $\frac{2b^{4}}{b^{2}+\frac{1}{4}\cdot\frac{c^{4}}{a^{2}}}$ = $\frac{2b^{2}}{1+\frac{1}{4}\cdot\frac{c^{4}}{a^{2}b^{2}}}$ = 8，
∴ $\frac{c^{4}}{a^{2}b^{2}}$ = $\frac{9}{4}$，
∴ a = 5，
∴ $\frac{a}{b}$ = 2.
【二级结论】在椭圆$\frac{x^{2}}{a^{2}}$ + $\frac{y^{2}}{b^{2}}$ = 1（a＞b＞0）中，点P为椭圆上一点.
如图，设∠PF₁F₂ = α，则|PF₁| = $\frac{b^{2}}{a - c\cos\alpha}$，|MF₁| = $\frac{b^{2}}{a + c\cos\alpha}$，
$\frac{1}{|PF₁|}$ + $\frac{1}{|MF₁|}$ = $\frac{2a}{b^{2}}$，
|MP| = $\frac{2ab^{2}}{a^{2}-c^{2}\cos^{2}\alpha}$.

证明：
在△PF₁F₂中，根据余弦定理，有|PF₂|² = |PF₁|² + |F₁F₂|² - 2|PF₁|·|F₁F₂|·cosα，
由椭圆定义|PF₁| + |PF₂| = 2a得(2a - |PF₁|)² = |PF₁|² + 4c² - 4ccosα·|PF₁|，
整理得|PF₁| = $\frac{b^{2}}{a - c\cos\alpha}$.
在△MF₁F₂中，|MF₂|² = |MF₁|² + |F₁F₂|² - 2|MF₁|·|F₁F₂|·cos(π - α) = (2a - |MF₁|)²，
整理得|MF₁| = $\frac{b^{2}}{a + c\cos\alpha}$.
所以$\frac{1}{|PF₁|}$ + $\frac{1}{|MF₁|}$ = $\frac{2a}{b^{2}}$，
|MP| = |MF₁| + |PF₁| = $\frac{2ab^{2}}{a^{2}-c^{2}\cos^{2}\alpha}$.

8. [武汉大学2022强基计划]已知F为椭圆C:$\frac{x^{2}}{9}+\frac{y^{2}}{4}=1$的左焦点,P为椭圆C上的一点.
(1)作正方形FPAB(F,P,A,B按逆时针方向排列),当点P沿着椭圆运动一周,求动点B的轨迹方程.
(2)设Q(3,2)为椭圆外一点,求$|PQ|+|PF|$的取值范围.

答案：
【解】
(1)如图所示，将椭圆C绕其左焦点F(-$\sqrt{5}$，0)逆时针旋转90°，得到椭圆C′.

注意到在正方形FPAB中，点B也可以看成是由点P绕点F逆时针旋转90°形成，由于点P在椭圆C上运动，则点B在椭圆C′上运动. 因此求点B的轨迹方程，也就是求椭圆C′的方程.
注意到椭圆C′的中心坐标为(-$\sqrt{5}$，$\sqrt{5}$)，
从而C′的方程为$\frac{(x + \sqrt{5})^{2}}{4}$ + $\frac{(y - \sqrt{5})^{2}}{9}$ = 1.
(2)如图所示，|PQ| + |PF| ≥ |QF| = $\sqrt{(3+\sqrt{5})^{2}+2^{2}}$ = $\sqrt{3+\sqrt{15}}$，
当且仅当P，F，Q三点共线，且P在线段FQ上，即P运动到P₁位置时，等号成立.
记椭圆C的右焦点为E($\sqrt{5}$，0)，
注意到|PQ| + |PF| = |PQ| + (2a - |PE|) = |PQ| - |PE| + 6，
显然有|PQ| - |PE| ≤ |QE| = $\sqrt{(3-\sqrt{5})^{2}+2^{2}}$ = $\sqrt{15}-\sqrt{3}$，
从而|PQ| + |PF| ≤ 6 + $\sqrt{15}-\sqrt{3}$，
当且仅当P，E，Q三点共线，且E在线段PQ上，即P运动到P₂位置时，等号成立.
于是可得$\sqrt{3+\sqrt{15}}$ ≤ |PQ| + |PF| ≤ 6 + $\sqrt{15}-\sqrt{3}$.
故|PQ| + |PF|的取值范围为[$\sqrt{3+\sqrt{15}}$，6 + $\sqrt{15}-\sqrt{3}$].