2024年高中必刷题高二数学选择性必修第一册人教B版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2024年高中必刷题高二数学选择性必修第一册人教B版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第27页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
1.[全国乙理2022·7,5分]在正方体ABCD - A₁B₁C₁D₁中,E,F分别为AB,BC的中点,则 ( )
A.平面B₁EF⊥平面BDD₁
B.平面B₁EF⊥平面A₁BD
C.平面B₁EF//平面A₁AC
D.平面B₁EF//平面A₁C₁D
A.平面B₁EF⊥平面BDD₁
B.平面B₁EF⊥平面A₁BD
C.平面B₁EF//平面A₁AC
D.平面B₁EF//平面A₁C₁D
答案:




2.(多选)[全国新高考Ⅰ2021·12,5分]在正三棱柱ABC - A₁B₁C₁中,AB = AA₁ = 1,点P满足$\overrightarrow{BP}=\lambda\overrightarrow{BC}+\mu\overrightarrow{BB_{1}}$,其中$\lambda\in[0,1],\mu\in[0,1]$,则 ( )
A.当$\lambda = 1$时,△AB₁P的周长为定值
B.当$\mu = 1$时,三棱锥P - A₁BC的体积为定值
C.当$\lambda=\frac{1}{2}$时,有且仅有一个点P,使得A₁P⊥BP
D.当$\mu=\frac{1}{2}$时,有且仅有一个点P,使得A₁B⊥平面AB₁P
A.当$\lambda = 1$时,△AB₁P的周长为定值
B.当$\mu = 1$时,三棱锥P - A₁BC的体积为定值
C.当$\lambda=\frac{1}{2}$时,有且仅有一个点P,使得A₁P⊥BP
D.当$\mu=\frac{1}{2}$时,有且仅有一个点P,使得A₁B⊥平面AB₁P
答案:
BD【解析】易知点P在矩形BCC₁B₁内部(含边界)。
对于A,当λ = 1时,$\overrightarrow{BP}=\overrightarrow{BC}+\mu\overrightarrow{BB_{1}}=\overrightarrow{BC}+\mu\overrightarrow{CC_{1}}$,即此时P∈线段CC₁。 当μ = 0时,点P与点C重合,此时△AB₁P的周长为AB₁ + AC + B₁C = $2\sqrt{2}+1$;当μ = $\frac{1}{2}$时,点P为线段CC₁的中点,此时AP = B₁P = $\sqrt{1^{2}+(\frac{1}{2})^{2}}=\frac{\sqrt{5}}{2}$,△AB₁P的周长为AB₁ + AP + B₁P = $\sqrt{2}+\frac{\sqrt{5}}{2}+\frac{\sqrt{5}}{2}=\sqrt{2}+\sqrt{5}$。 所以△AB₁P的周长不是定值,故A错误;
对于B,当μ = 1时,$\overrightarrow{BP}=\lambda\overrightarrow{BC}+\overrightarrow{BB_{1}}=\overrightarrow{BB_{1}}+\lambda\overrightarrow{B_{1}C_{1}}$,故此时P点轨迹为线段B₁C₁,而B₁C₁//BC,又B₁C₁⊄平面A₁BC,BC⊂平面A₁BC,所以B₁C₁//平面A₁BC,则有点P到平面A₁BC的距离为定值,又△A₁BC的面积为定值,所以三棱锥P - A₁BC的体积为定值,故B正确。
对于C,当λ = $\frac{1}{2}$时,$\overrightarrow{BP}=\frac{1}{2}\overrightarrow{BC}+\mu\overrightarrow{BB_{1}}$,取BC,B₁C₁的中点分别为Q,H,则$\overrightarrow{BP}=\overrightarrow{BQ}+\mu\overrightarrow{QH}$,所以点P轨迹为线段QH,不妨建立如图所示的空间直角坐标系,

则A₁($\frac{\sqrt{3}}{2}$,0,1),P(0,0,μ),B(0,$\frac{1}{2}$,0),则$\overrightarrow{A_{1}P}=(-\frac{\sqrt{3}}{2},0,\mu - 1)$,$\overrightarrow{BP}=(0,-\frac{1}{2},\mu)$,$\overrightarrow{A_{1}P}\cdot\overrightarrow{BP}=\mu(\mu - 1)=0$,所以μ = 0或μ = 1。 故点H,Q均满足,故C错误;
对于D,当μ = $\frac{1}{2}$时,$\overrightarrow{BP}=\lambda\overrightarrow{BC}+\frac{1}{2}\overrightarrow{BB_{1}}$,取BB₁,CC₁的中点分别为M,N,则$\overrightarrow{BP}=\overrightarrow{BM}+\lambda\overrightarrow{MN}$,所以点P轨迹为线段MN。 设P(0,y₀,$\frac{1}{2}$),因为A($\frac{\sqrt{3}}{2}$,0,0),所以$\overrightarrow{AP}=(-\frac{\sqrt{3}}{2},y_{0},\frac{1}{2})$,$\overrightarrow{A_{1}B}=(-\frac{\sqrt{3}}{2},\frac{1}{2},-1)$,因为A₁B⊥平面AB₁P,所以A₁B⊥AP,所以$\overrightarrow{AP}\cdot\overrightarrow{A_{1}B}=\frac{3}{4}+\frac{1}{2}y_{0}-\frac{1}{2}=0\Rightarrow y_{0}=-\frac{1}{2}$,此时点P与点N重合,故D正确。 故选BD。
BD【解析】易知点P在矩形BCC₁B₁内部(含边界)。
对于A,当λ = 1时,$\overrightarrow{BP}=\overrightarrow{BC}+\mu\overrightarrow{BB_{1}}=\overrightarrow{BC}+\mu\overrightarrow{CC_{1}}$,即此时P∈线段CC₁。 当μ = 0时,点P与点C重合,此时△AB₁P的周长为AB₁ + AC + B₁C = $2\sqrt{2}+1$;当μ = $\frac{1}{2}$时,点P为线段CC₁的中点,此时AP = B₁P = $\sqrt{1^{2}+(\frac{1}{2})^{2}}=\frac{\sqrt{5}}{2}$,△AB₁P的周长为AB₁ + AP + B₁P = $\sqrt{2}+\frac{\sqrt{5}}{2}+\frac{\sqrt{5}}{2}=\sqrt{2}+\sqrt{5}$。 所以△AB₁P的周长不是定值,故A错误;
对于B,当μ = 1时,$\overrightarrow{BP}=\lambda\overrightarrow{BC}+\overrightarrow{BB_{1}}=\overrightarrow{BB_{1}}+\lambda\overrightarrow{B_{1}C_{1}}$,故此时P点轨迹为线段B₁C₁,而B₁C₁//BC,又B₁C₁⊄平面A₁BC,BC⊂平面A₁BC,所以B₁C₁//平面A₁BC,则有点P到平面A₁BC的距离为定值,又△A₁BC的面积为定值,所以三棱锥P - A₁BC的体积为定值,故B正确。
对于C,当λ = $\frac{1}{2}$时,$\overrightarrow{BP}=\frac{1}{2}\overrightarrow{BC}+\mu\overrightarrow{BB_{1}}$,取BC,B₁C₁的中点分别为Q,H,则$\overrightarrow{BP}=\overrightarrow{BQ}+\mu\overrightarrow{QH}$,所以点P轨迹为线段QH,不妨建立如图所示的空间直角坐标系,

则A₁($\frac{\sqrt{3}}{2}$,0,1),P(0,0,μ),B(0,$\frac{1}{2}$,0),则$\overrightarrow{A_{1}P}=(-\frac{\sqrt{3}}{2},0,\mu - 1)$,$\overrightarrow{BP}=(0,-\frac{1}{2},\mu)$,$\overrightarrow{A_{1}P}\cdot\overrightarrow{BP}=\mu(\mu - 1)=0$,所以μ = 0或μ = 1。 故点H,Q均满足,故C错误;
对于D,当μ = $\frac{1}{2}$时,$\overrightarrow{BP}=\lambda\overrightarrow{BC}+\frac{1}{2}\overrightarrow{BB_{1}}$,取BB₁,CC₁的中点分别为M,N,则$\overrightarrow{BP}=\overrightarrow{BM}+\lambda\overrightarrow{MN}$,所以点P轨迹为线段MN。 设P(0,y₀,$\frac{1}{2}$),因为A($\frac{\sqrt{3}}{2}$,0,0),所以$\overrightarrow{AP}=(-\frac{\sqrt{3}}{2},y_{0},\frac{1}{2})$,$\overrightarrow{A_{1}B}=(-\frac{\sqrt{3}}{2},\frac{1}{2},-1)$,因为A₁B⊥平面AB₁P,所以A₁B⊥AP,所以$\overrightarrow{AP}\cdot\overrightarrow{A_{1}B}=\frac{3}{4}+\frac{1}{2}y_{0}-\frac{1}{2}=0\Rightarrow y_{0}=-\frac{1}{2}$,此时点P与点N重合,故D正确。 故选BD。
3.[全国新课标Ⅰ2023·18,12分]如图,在正四棱柱ABCD - A₁B₁C₁D₁中,AB = 2,AA₁ = 4.点A₂,B₂,C₂,D₂分别在棱AA₁,BB₁,CC₁,DD₁上,AA₂ = 1,BB₂ = DD₂ = 2,CC₂ = 3.
(1)证明:B₂C₂//A₂D₂;
(2)点P在棱BB₁上,当二面角P - A₂C₂ - D₂为150°时,求B₂P.

(1)证明:B₂C₂//A₂D₂;
(2)点P在棱BB₁上,当二面角P - A₂C₂ - D₂为150°时,求B₂P.

答案:
(1)【证明】如图,以CD,CB,CC₁所在直线分别为x,y,z轴,建立空间直角坐标系。

因为AB = 2,AA₁ = 4,AA₂ = 1,BB₂ = DD₂ = 2,CC₂ = 3,所以A₂(2,2,1),B₂(0,2,2),C₂(0,0,3),D₂(2,0,2),所以$\overrightarrow{A_{2}D_{2}}=\overrightarrow{B_{2}C_{2}}=(0,-2,1)$,又A₂,D₂,B₂,C₂四点不共线,所以B₂C₂//A₂D₂。
【多种解法】如图,过点A₂作A₂E⊥BB₁于点E,过点D₂作D₂F⊥CC₁于点F,在正四棱柱ABCD - A₁B₁C₁D₁中,AB = 2,AA₁ = 4,点A₂,B₂,C₂,D₂分别在棱AA₁,BB₁,CC₁,DD₁上,且AA₂ = 1,BB₂ = DD₂ = 2,CC₂ = 3,所以A₂E⊥D₂F,B₂E//C₂F,所以四边形A₂EFD₂,B₂C₂FE均为平行四边形,所以A₂D₂//EF,B₂C₂//EF,所以B₂C₂//A₂D₂。

(2)【解】设P(0,2,a)(0≤a≤4),由
(1)中建系可知A₂(2,2,1),C₂(0,0,3),D₂(2,0,2),则$\overrightarrow{A_{2}C_{2}}=(-2,-2,2)$,$\overrightarrow{A_{2}D_{2}}=(0,-2,1)$,$\overrightarrow{A_{2}P}=(-2,0,a - 1)$。 设平面A₂C₂D₂的法向量为$\boldsymbol{m}=(x_{1},y_{1},z_{1})$,所以$\begin{cases}\overrightarrow{A_{2}C_{2}}\cdot\boldsymbol{m}=0\\\overrightarrow{A_{2}D_{2}}\cdot\boldsymbol{m}=0\end{cases}$,即$\begin{cases}-2x_{1}-2y_{1}+2z_{1}=0\\-2y_{1}+z_{1}=0\end{cases}$,取y₁ = 1,可得x₁ = 1,z₁ = 2,所以$\boldsymbol{m}=(1,1,2)$。
设平面PA₂C₂的法向量为$\boldsymbol{n}=(x_{2},y_{2},z_{2})$,所以$\begin{cases}\overrightarrow{A_{2}C_{2}}\cdot\boldsymbol{n}=0\\\overrightarrow{A_{2}P}\cdot\boldsymbol{n}=0\end{cases}$,即$\begin{cases}-2x_{2}-2y_{2}+2z_{2}=0\\-2x_{2}+(a - 1)z_{2}=0\end{cases}$,取z₂ = 1,可得x₂ = $\frac{a - 1}{2}$,y₂ = $\frac{3 - a}{2}$,所以$\boldsymbol{n}=(\frac{a - 1}{2},\frac{3 - a}{2},1)$。
因为二面角P - A₂C₂ - D₂为150°,所以|$\cos\langle\boldsymbol{m},\boldsymbol{n}\rangle$| = $\frac{|\boldsymbol{m}\cdot\boldsymbol{n}|}{|\boldsymbol{m}||\boldsymbol{n}|}=\frac{\sqrt{3}}{2}$,即
$\frac{|\frac{a - 1}{2}+\frac{3 - a}{2}+2|}{\sqrt{1^{2}+1^{2}+2^{2}}\cdot\sqrt{(\frac{a - 1}{2})^{2}+(\frac{3 - a}{2})^{2}+1^{2}}}=\frac{\sqrt{3}}{2}$,解得a = 1或a = 3,所以点P为B₂B的中点或B₂B₁的中点,即B₂P = 1。
(1)【证明】如图,以CD,CB,CC₁所在直线分别为x,y,z轴,建立空间直角坐标系。

因为AB = 2,AA₁ = 4,AA₂ = 1,BB₂ = DD₂ = 2,CC₂ = 3,所以A₂(2,2,1),B₂(0,2,2),C₂(0,0,3),D₂(2,0,2),所以$\overrightarrow{A_{2}D_{2}}=\overrightarrow{B_{2}C_{2}}=(0,-2,1)$,又A₂,D₂,B₂,C₂四点不共线,所以B₂C₂//A₂D₂。
【多种解法】如图,过点A₂作A₂E⊥BB₁于点E,过点D₂作D₂F⊥CC₁于点F,在正四棱柱ABCD - A₁B₁C₁D₁中,AB = 2,AA₁ = 4,点A₂,B₂,C₂,D₂分别在棱AA₁,BB₁,CC₁,DD₁上,且AA₂ = 1,BB₂ = DD₂ = 2,CC₂ = 3,所以A₂E⊥D₂F,B₂E//C₂F,所以四边形A₂EFD₂,B₂C₂FE均为平行四边形,所以A₂D₂//EF,B₂C₂//EF,所以B₂C₂//A₂D₂。

(2)【解】设P(0,2,a)(0≤a≤4),由
(1)中建系可知A₂(2,2,1),C₂(0,0,3),D₂(2,0,2),则$\overrightarrow{A_{2}C_{2}}=(-2,-2,2)$,$\overrightarrow{A_{2}D_{2}}=(0,-2,1)$,$\overrightarrow{A_{2}P}=(-2,0,a - 1)$。 设平面A₂C₂D₂的法向量为$\boldsymbol{m}=(x_{1},y_{1},z_{1})$,所以$\begin{cases}\overrightarrow{A_{2}C_{2}}\cdot\boldsymbol{m}=0\\\overrightarrow{A_{2}D_{2}}\cdot\boldsymbol{m}=0\end{cases}$,即$\begin{cases}-2x_{1}-2y_{1}+2z_{1}=0\\-2y_{1}+z_{1}=0\end{cases}$,取y₁ = 1,可得x₁ = 1,z₁ = 2,所以$\boldsymbol{m}=(1,1,2)$。
设平面PA₂C₂的法向量为$\boldsymbol{n}=(x_{2},y_{2},z_{2})$,所以$\begin{cases}\overrightarrow{A_{2}C_{2}}\cdot\boldsymbol{n}=0\\\overrightarrow{A_{2}P}\cdot\boldsymbol{n}=0\end{cases}$,即$\begin{cases}-2x_{2}-2y_{2}+2z_{2}=0\\-2x_{2}+(a - 1)z_{2}=0\end{cases}$,取z₂ = 1,可得x₂ = $\frac{a - 1}{2}$,y₂ = $\frac{3 - a}{2}$,所以$\boldsymbol{n}=(\frac{a - 1}{2},\frac{3 - a}{2},1)$。
因为二面角P - A₂C₂ - D₂为150°,所以|$\cos\langle\boldsymbol{m},\boldsymbol{n}\rangle$| = $\frac{|\boldsymbol{m}\cdot\boldsymbol{n}|}{|\boldsymbol{m}||\boldsymbol{n}|}=\frac{\sqrt{3}}{2}$,即
$\frac{|\frac{a - 1}{2}+\frac{3 - a}{2}+2|}{\sqrt{1^{2}+1^{2}+2^{2}}\cdot\sqrt{(\frac{a - 1}{2})^{2}+(\frac{3 - a}{2})^{2}+1^{2}}}=\frac{\sqrt{3}}{2}$,解得a = 1或a = 3,所以点P为B₂B的中点或B₂B₁的中点,即B₂P = 1。
4.[全国乙理2023·19,12分]如图,在三棱锥P - ABC中,AB⊥BC,AB = 2,BC = 2$\sqrt{2}$,PB = PC=$\sqrt{6}$,BP,AP,BC的中点分别为D,E,O,AD=$\sqrt{5}$DO,点F在AC上,BF⊥AO.
(1)证明:EF//平面ADO;
(2)证明:平面ADO⊥平面BEF;
(3)求二面角D - AO - C的正弦值.
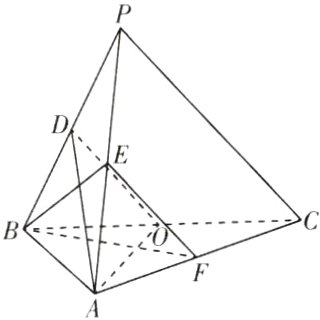
(1)证明:EF//平面ADO;
(2)证明:平面ADO⊥平面BEF;
(3)求二面角D - AO - C的正弦值.

答案:
(1)【证明】连接DE,OF,如图所示。
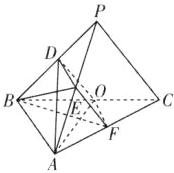
设$\overrightarrow{AF}=\lambda\overrightarrow{AC}(0\leq\lambda\leq1)$,则$\overrightarrow{BF}=\overrightarrow{BA}+\overrightarrow{AF}=\overrightarrow{BA}+\lambda\overrightarrow{AC}=\overrightarrow{BA}+\lambda(\overrightarrow{AB}+\overrightarrow{BC})=(1 - \lambda)\overrightarrow{BA}+\lambda\overrightarrow{BC}$,$\overrightarrow{AO}=\overrightarrow{AB}+\overrightarrow{BO}=-\overrightarrow{BA}+\frac{1}{2}\overrightarrow{BC}$。 因为BF⊥AO,所以$\overrightarrow{BF}\cdot\overrightarrow{AO}=[(1 - \lambda)\overrightarrow{BA}+\lambda\overrightarrow{BC}]\cdot(-\overrightarrow{BA}+\frac{1}{2}\overrightarrow{BC})=(\lambda - 1)|\overrightarrow{BA}|^{2}+\frac{1}{2}\lambda\cdot|\overrightarrow{BC}|^{2}=4(\lambda - 1)+4\lambda = 0$,解得$\lambda=\frac{1}{2}$,即$\overrightarrow{AF}=\frac{1}{2}\overrightarrow{AC}$,故F为AC的中点。 又O为BC的中点,所以OF//AB,OF = $\frac{1}{2}$AB。 因为D,E分别为PB,PA的中点,所以DE//AB,DE = $\frac{1}{2}$AB,所以DE//OF,DE = OF,所以四边形DEFO为平行四边形,所以EF//DO。 因为EF⊄平面ADO,DO⊂平面ADO,所以EF//平面ADO。
(2)【证明】由
(1)知BF = $\frac{1}{2}$AC = $\sqrt{3}$,AO = $\sqrt{6}$,DO = EF = $\frac{\sqrt{6}}{2}$,AD = $\sqrt{5}DO=\frac{\sqrt{30}}{2}$,BD = $\frac{\sqrt{6}}{2}$,所以AO² + DO² = AD²,所以AO⊥DO。 因为EF//DO,所以AO⊥EF。 又AO⊥BF,BF∩EF = F,BF,EF⊂平面BEF,所以AO⊥平面BEF。 又因为AO⊂平面ADO,所以平面ADO⊥平面BEF。
(3)【解】以B为原点,BA所在直线为x轴,BC所在直线为y轴,建立如图所示的空间直角坐标系,则B(0,0,0),A(2,0,0),O(0,$\sqrt{2}$,0),C(0,2$\sqrt{2}$,0)。
因为$\cos\angle ADB=-\cos\angle ADP$,
$\frac{(\frac{\sqrt{6}}{2})^{2}+(\frac{\sqrt{30}}{2})^{2}-2^{2}}{2\times\frac{\sqrt{6}}{2}\times\frac{\sqrt{30}}{2}}=-\frac{(\frac{\sqrt{6}}{2})^{2}+(\frac{\sqrt{30}}{2})^{2}-PA^{2}}{2\times\frac{\sqrt{6}}{2}\times\frac{\sqrt{30}}{2}}$,
解得PA = $\sqrt{14}$。
设P(x,y,z),由PB = PC = $\sqrt{6}$,PA = $\sqrt{14}$,得$\begin{cases}x^{2}+y^{2}+z^{2}=6\\x^{2}+(y - 2\sqrt{2})^{2}+z^{2}=6\\(x - 2)^{2}+y^{2}+z^{2}=14\end{cases}$,
解得$\begin{cases}x=-1\\y=\sqrt{2}\\z=\sqrt{3}\end{cases}$(舍负),
故P(-1,$\sqrt{2}$,$\sqrt{3}$),D(-$\frac{1}{2}$,$\frac{\sqrt{2}}{2}$,$\frac{\sqrt{3}}{2}$)。
取平面AOC的法向量为$\boldsymbol{m}_{1}=(0,0,1)$。
设平面AOD的法向量为$\boldsymbol{m}_{2}=(x_{2},y_{2},z_{2})$,由$\overrightarrow{AO}=(-2,\sqrt{2},0)$,$\overrightarrow{OD}=(-\frac{1}{2},-\frac{\sqrt{2}}{2},\frac{\sqrt{3}}{2})$,
得$\begin{cases}-2x_{2}+\sqrt{2}y_{2}=0\\-\frac{1}{2}x_{2}-\frac{\sqrt{2}}{2}y_{2}+\frac{\sqrt{3}}{2}z_{2}=0\end{cases}$,
令x₂ = 1,则$\boldsymbol{m}_{2}=(1,\sqrt{2},\sqrt{3})$。
所以$\cos\langle\boldsymbol{m}_{1},\boldsymbol{m}_{2}\rangle=\frac{\boldsymbol{m}_{1}\cdot\boldsymbol{m}_{2}}{|\boldsymbol{m}_{1}||\boldsymbol{m}_{2}|}=\frac{\sqrt{3}}{\sqrt{1 + 2+3}}=\frac{\sqrt{2}}{2}$,所以二面角D - AO - C的正弦值为$\sqrt{1 - (\frac{\sqrt{2}}{2})^{2}}=\frac{\sqrt{2}}{2}$。
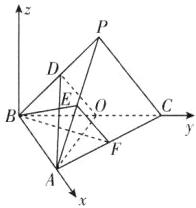
【多种解法】
(3)如图所示,过点O作OH//BF交AC于点H,连接DH。 由AO⊥BF知AO⊥OH,且FH = $\frac{1}{3}$AH,又由
(2)知AO⊥OD,故∠DOH为二面角D - AO - C的平面角。
设AD∩BE = G,连接GF。
因为D,E分别为PB,PA的中点,故点G为△PAB的重心,所以DG = $\frac{1}{3}$AD,又FH = $\frac{1}{3}$AH,
所以DH//GF,DH = $\frac{3}{2}$GF。
在△ABD和△ABP中,由余弦定理得
$\cos\angle ABD=\frac{4+\frac{3}{2}-\frac{15}{2}}{2\times2\times\frac{\sqrt{6}}{2}}=\frac{4 + 6 - PA^{2}}{2\times2\times\sqrt{6}}$,解得PA = $\sqrt{14}$,同理可得BE = $\frac{\sqrt{6}}{2}$。
故BE² + EF² = BF² = 3,所以BE⊥EF,故GF² = ($\frac{1}{3}\times\frac{\sqrt{6}}{2}$)² + ($\frac{\sqrt{6}}{2}$)² = $\frac{5}{3}$,所以GF = $\frac{\sqrt{15}}{3}$,
所以DH = $\frac{3}{2}\times\frac{\sqrt{15}}{3}=\frac{\sqrt{15}}{2}$。
在△DOH中,OH = $\frac{1}{2}$BF = $\frac{\sqrt{3}}{2}$,OD = $\frac{\sqrt{6}}{2}$,DH = $\frac{\sqrt{15}}{2}$,所以$\cos\angle DOH=\frac{\frac{6}{4}+\frac{3}{4}-\frac{15}{4}}{2\times\frac{\sqrt{6}}{2}\times\frac{\sqrt{3}}{2}}=-\frac{\sqrt{2}}{2}$,故$\sin\angle DOH=\sqrt{1-\cos^{2}\angle DOH}=\frac{\sqrt{2}}{2}$,即二面角D - AO - C的正弦值为$\frac{\sqrt{2}}{2}$。

(1)【证明】连接DE,OF,如图所示。

设$\overrightarrow{AF}=\lambda\overrightarrow{AC}(0\leq\lambda\leq1)$,则$\overrightarrow{BF}=\overrightarrow{BA}+\overrightarrow{AF}=\overrightarrow{BA}+\lambda\overrightarrow{AC}=\overrightarrow{BA}+\lambda(\overrightarrow{AB}+\overrightarrow{BC})=(1 - \lambda)\overrightarrow{BA}+\lambda\overrightarrow{BC}$,$\overrightarrow{AO}=\overrightarrow{AB}+\overrightarrow{BO}=-\overrightarrow{BA}+\frac{1}{2}\overrightarrow{BC}$。 因为BF⊥AO,所以$\overrightarrow{BF}\cdot\overrightarrow{AO}=[(1 - \lambda)\overrightarrow{BA}+\lambda\overrightarrow{BC}]\cdot(-\overrightarrow{BA}+\frac{1}{2}\overrightarrow{BC})=(\lambda - 1)|\overrightarrow{BA}|^{2}+\frac{1}{2}\lambda\cdot|\overrightarrow{BC}|^{2}=4(\lambda - 1)+4\lambda = 0$,解得$\lambda=\frac{1}{2}$,即$\overrightarrow{AF}=\frac{1}{2}\overrightarrow{AC}$,故F为AC的中点。 又O为BC的中点,所以OF//AB,OF = $\frac{1}{2}$AB。 因为D,E分别为PB,PA的中点,所以DE//AB,DE = $\frac{1}{2}$AB,所以DE//OF,DE = OF,所以四边形DEFO为平行四边形,所以EF//DO。 因为EF⊄平面ADO,DO⊂平面ADO,所以EF//平面ADO。
(2)【证明】由
(1)知BF = $\frac{1}{2}$AC = $\sqrt{3}$,AO = $\sqrt{6}$,DO = EF = $\frac{\sqrt{6}}{2}$,AD = $\sqrt{5}DO=\frac{\sqrt{30}}{2}$,BD = $\frac{\sqrt{6}}{2}$,所以AO² + DO² = AD²,所以AO⊥DO。 因为EF//DO,所以AO⊥EF。 又AO⊥BF,BF∩EF = F,BF,EF⊂平面BEF,所以AO⊥平面BEF。 又因为AO⊂平面ADO,所以平面ADO⊥平面BEF。
(3)【解】以B为原点,BA所在直线为x轴,BC所在直线为y轴,建立如图所示的空间直角坐标系,则B(0,0,0),A(2,0,0),O(0,$\sqrt{2}$,0),C(0,2$\sqrt{2}$,0)。
因为$\cos\angle ADB=-\cos\angle ADP$,
$\frac{(\frac{\sqrt{6}}{2})^{2}+(\frac{\sqrt{30}}{2})^{2}-2^{2}}{2\times\frac{\sqrt{6}}{2}\times\frac{\sqrt{30}}{2}}=-\frac{(\frac{\sqrt{6}}{2})^{2}+(\frac{\sqrt{30}}{2})^{2}-PA^{2}}{2\times\frac{\sqrt{6}}{2}\times\frac{\sqrt{30}}{2}}$,
解得PA = $\sqrt{14}$。
设P(x,y,z),由PB = PC = $\sqrt{6}$,PA = $\sqrt{14}$,得$\begin{cases}x^{2}+y^{2}+z^{2}=6\\x^{2}+(y - 2\sqrt{2})^{2}+z^{2}=6\\(x - 2)^{2}+y^{2}+z^{2}=14\end{cases}$,
解得$\begin{cases}x=-1\\y=\sqrt{2}\\z=\sqrt{3}\end{cases}$(舍负),
故P(-1,$\sqrt{2}$,$\sqrt{3}$),D(-$\frac{1}{2}$,$\frac{\sqrt{2}}{2}$,$\frac{\sqrt{3}}{2}$)。
取平面AOC的法向量为$\boldsymbol{m}_{1}=(0,0,1)$。
设平面AOD的法向量为$\boldsymbol{m}_{2}=(x_{2},y_{2},z_{2})$,由$\overrightarrow{AO}=(-2,\sqrt{2},0)$,$\overrightarrow{OD}=(-\frac{1}{2},-\frac{\sqrt{2}}{2},\frac{\sqrt{3}}{2})$,
得$\begin{cases}-2x_{2}+\sqrt{2}y_{2}=0\\-\frac{1}{2}x_{2}-\frac{\sqrt{2}}{2}y_{2}+\frac{\sqrt{3}}{2}z_{2}=0\end{cases}$,
令x₂ = 1,则$\boldsymbol{m}_{2}=(1,\sqrt{2},\sqrt{3})$。
所以$\cos\langle\boldsymbol{m}_{1},\boldsymbol{m}_{2}\rangle=\frac{\boldsymbol{m}_{1}\cdot\boldsymbol{m}_{2}}{|\boldsymbol{m}_{1}||\boldsymbol{m}_{2}|}=\frac{\sqrt{3}}{\sqrt{1 + 2+3}}=\frac{\sqrt{2}}{2}$,所以二面角D - AO - C的正弦值为$\sqrt{1 - (\frac{\sqrt{2}}{2})^{2}}=\frac{\sqrt{2}}{2}$。

【多种解法】
(3)如图所示,过点O作OH//BF交AC于点H,连接DH。 由AO⊥BF知AO⊥OH,且FH = $\frac{1}{3}$AH,又由
(2)知AO⊥OD,故∠DOH为二面角D - AO - C的平面角。
设AD∩BE = G,连接GF。
因为D,E分别为PB,PA的中点,故点G为△PAB的重心,所以DG = $\frac{1}{3}$AD,又FH = $\frac{1}{3}$AH,
所以DH//GF,DH = $\frac{3}{2}$GF。
在△ABD和△ABP中,由余弦定理得
$\cos\angle ABD=\frac{4+\frac{3}{2}-\frac{15}{2}}{2\times2\times\frac{\sqrt{6}}{2}}=\frac{4 + 6 - PA^{2}}{2\times2\times\sqrt{6}}$,解得PA = $\sqrt{14}$,同理可得BE = $\frac{\sqrt{6}}{2}$。
故BE² + EF² = BF² = 3,所以BE⊥EF,故GF² = ($\frac{1}{3}\times\frac{\sqrt{6}}{2}$)² + ($\frac{\sqrt{6}}{2}$)² = $\frac{5}{3}$,所以GF = $\frac{\sqrt{15}}{3}$,
所以DH = $\frac{3}{2}\times\frac{\sqrt{15}}{3}=\frac{\sqrt{15}}{2}$。
在△DOH中,OH = $\frac{1}{2}$BF = $\frac{\sqrt{3}}{2}$,OD = $\frac{\sqrt{6}}{2}$,DH = $\frac{\sqrt{15}}{2}$,所以$\cos\angle DOH=\frac{\frac{6}{4}+\frac{3}{4}-\frac{15}{4}}{2\times\frac{\sqrt{6}}{2}\times\frac{\sqrt{3}}{2}}=-\frac{\sqrt{2}}{2}$,故$\sin\angle DOH=\sqrt{1-\cos^{2}\angle DOH}=\frac{\sqrt{2}}{2}$,即二面角D - AO - C的正弦值为$\frac{\sqrt{2}}{2}$。

5.[全国乙理2022·18,12分]如图,四面体ABCD中,AD⊥CD,AD = CD,∠ADB = ∠BDC,E为AC的中点.
(1)证明:平面BED⊥平面ACD;
(2)设AB = BD = 2,∠ACB = 60°,点F在BD上,当△AFC的面积最小时,求CF与平面ABD所成的角的正弦值.

(1)证明:平面BED⊥平面ACD;
(2)设AB = BD = 2,∠ACB = 60°,点F在BD上,当△AFC的面积最小时,求CF与平面ABD所成的角的正弦值.

答案:
(1)【证明】因为在△ABD和△CBD中,AD = DC,∠ADB = ∠CDB,DB = DB,所以△ABD≌△CBD,所以AB = CB。 又因为E为AC的中点,所以BE⊥AC。 因为AD = DC,E为AC的中点,所以DE⊥AC。 又BE∩DE = E,所以AC⊥平面BED。 又因为AC⊂平面ACD,所以平面BED⊥平面ACD。
(2)【解】由
(1)得AB = CB,又∠ACB = 60°,所以△ABC为等边三角形。 因为AB = BD = 2,所以AB = CB = AC = 2,BE = $\sqrt{3}$。 因为AD⊥DC,AD = DC,所以△ADC是等腰直角三角形,所以AD = CD = $\sqrt{2}$,DE = 1。 因为DE² + BE² = BD²,所以DE⊥BE,于是在△BED中,设h为△BED的边BD的高,则由等面积可得$\frac{1}{2}\times2\times h=\frac{1}{2}\times1\times\sqrt{3}$,即h = $\frac{\sqrt{3}}{2}$。 连接EF,由
(1)知AC⊥平面BED,又EF⊂平面BED,所以AC⊥EF,于是当EF⊥BD时,△ACF的面积最小,此时EF = h = $\frac{\sqrt{3}}{2}$,BF = $\frac{3}{2}$,DF = $\frac{1}{2}$,所以此时F为线段BD上靠近点D的四等分点。 以E为坐标原点建立如图所示的空间直角坐标系,则E(0,0,0),A(1,0,0),C(-1,0,0),B(0,$\sqrt{3}$,0),D(0,0,1),F(0,$\frac{\sqrt{3}}{4}$,$\frac{3}{4}$),所以$\overrightarrow{CF}=(1,\frac{\sqrt{3}}{4},\frac{3}{4})$,$\overrightarrow{AB}=(-1,\sqrt{3},0)$,$\overrightarrow{AD}=(-1,0,1)$。

设平面ABD的法向量为$\boldsymbol{n}=(x,y,z)$,则$\begin{cases}\boldsymbol{n}\cdot\overrightarrow{AB}=-x+\sqrt{3}y=0\\\boldsymbol{n}\cdot\overrightarrow{AD}=-x+z=0\end{cases}$,即x = $\sqrt{3}$y = z,令y = 1,则$\boldsymbol{n}=(\sqrt{3},1,\sqrt{3})$。 所以|$\cos\langle\boldsymbol{n},\overrightarrow{CF}\rangle$| = $\frac{|\boldsymbol{n}\cdot\overrightarrow{CF}|}{|\boldsymbol{n}||\overrightarrow{CF}|}=\frac{2\sqrt{3}}{\sqrt{1+\frac{3}{16}+\frac{9}{16}}\times\sqrt{3 + 1+3}}=\frac{4\sqrt{3}}{7}$,故直线CF与平面ABD所成的角的正弦值为$\frac{4\sqrt{3}}{7}$。
(1)【证明】因为在△ABD和△CBD中,AD = DC,∠ADB = ∠CDB,DB = DB,所以△ABD≌△CBD,所以AB = CB。 又因为E为AC的中点,所以BE⊥AC。 因为AD = DC,E为AC的中点,所以DE⊥AC。 又BE∩DE = E,所以AC⊥平面BED。 又因为AC⊂平面ACD,所以平面BED⊥平面ACD。
(2)【解】由
(1)得AB = CB,又∠ACB = 60°,所以△ABC为等边三角形。 因为AB = BD = 2,所以AB = CB = AC = 2,BE = $\sqrt{3}$。 因为AD⊥DC,AD = DC,所以△ADC是等腰直角三角形,所以AD = CD = $\sqrt{2}$,DE = 1。 因为DE² + BE² = BD²,所以DE⊥BE,于是在△BED中,设h为△BED的边BD的高,则由等面积可得$\frac{1}{2}\times2\times h=\frac{1}{2}\times1\times\sqrt{3}$,即h = $\frac{\sqrt{3}}{2}$。 连接EF,由
(1)知AC⊥平面BED,又EF⊂平面BED,所以AC⊥EF,于是当EF⊥BD时,△ACF的面积最小,此时EF = h = $\frac{\sqrt{3}}{2}$,BF = $\frac{3}{2}$,DF = $\frac{1}{2}$,所以此时F为线段BD上靠近点D的四等分点。 以E为坐标原点建立如图所示的空间直角坐标系,则E(0,0,0),A(1,0,0),C(-1,0,0),B(0,$\sqrt{3}$,0),D(0,0,1),F(0,$\frac{\sqrt{3}}{4}$,$\frac{3}{4}$),所以$\overrightarrow{CF}=(1,\frac{\sqrt{3}}{4},\frac{3}{4})$,$\overrightarrow{AB}=(-1,\sqrt{3},0)$,$\overrightarrow{AD}=(-1,0,1)$。

设平面ABD的法向量为$\boldsymbol{n}=(x,y,z)$,则$\begin{cases}\boldsymbol{n}\cdot\overrightarrow{AB}=-x+\sqrt{3}y=0\\\boldsymbol{n}\cdot\overrightarrow{AD}=-x+z=0\end{cases}$,即x = $\sqrt{3}$y = z,令y = 1,则$\boldsymbol{n}=(\sqrt{3},1,\sqrt{3})$。 所以|$\cos\langle\boldsymbol{n},\overrightarrow{CF}\rangle$| = $\frac{|\boldsymbol{n}\cdot\overrightarrow{CF}|}{|\boldsymbol{n}||\overrightarrow{CF}|}=\frac{2\sqrt{3}}{\sqrt{1+\frac{3}{16}+\frac{9}{16}}\times\sqrt{3 + 1+3}}=\frac{4\sqrt{3}}{7}$,故直线CF与平面ABD所成的角的正弦值为$\frac{4\sqrt{3}}{7}$。
查看更多完整答案,请扫码查看


