2024年高中必刷题高二数学选择性必修第一册人教B版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2024年高中必刷题高二数学选择性必修第一册人教B版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第24页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
9. 如图,正方体ABCD - A₁B₁C₁D₁的棱长为1,E是DD₁的中点,则下列说法正确的是 ( )
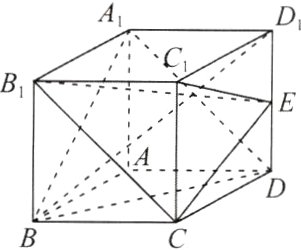
A. 直线B₁C//平面A₁BD
B. B₁C⊥BD₁
C. 三棱锥C₁ - B₁CE的体积为$\frac{1}{3}$
D. 直线B₁E与平面CDD₁C₁所成的角为60°

A. 直线B₁C//平面A₁BD
B. B₁C⊥BD₁
C. 三棱锥C₁ - B₁CE的体积为$\frac{1}{3}$
D. 直线B₁E与平面CDD₁C₁所成的角为60°
答案:
9.AB【解析】如图,建立空间直角坐标系,则$A(0,0,0),B(1,0,0),C(1,1,0),D(0,1,0),A_1(0,0,1),B_1(1,0,1),C_1(1,1,1),D_1(0,1,1),E(0,1,\frac{1}{2})$,所以$\overrightarrow{B_1C}=(0,1,-1),\overrightarrow{BD_1}=(-1,1,1),\overrightarrow{BD}=(-1,1,0),\overrightarrow{BA_1}=(-1,0,1)$.
对于A,设平面$A_1BD$的法向量为$\boldsymbol{n}=(x,y,z)$,则$\begin{cases}\boldsymbol{n}\cdot\overrightarrow{BA_1}=0\\\boldsymbol{n}\cdot\overrightarrow{BD}=0\end{cases}$,即$\begin{cases}-x + z = 0\\-x + y = 0\end{cases}$,取$\boldsymbol{n}=(1,1,1)$,
则$\boldsymbol{n}\cdot\overrightarrow{B_1C}=1\times0 + 1\times1 + 1\times(-1)=0$,即$\boldsymbol{n}\perp\overrightarrow{B_1C}$,又直线$B_1C\not\subset$平面$A_1BD$,所以直线$B_1C//$平面$A_1BD$,故A正确;
对于B,因为$\overrightarrow{B_1C}\cdot\overrightarrow{BD_1}=0\times(-1)+1\times1+(-1)\times1 = 0$,所以$\overrightarrow{B_1C}\perp\overrightarrow{BD_1}$,即$B_1C\perp BD_1$,故B正确;
对于C,$V_{C_1 - B_1CE}=V_{B_1 - C_1CE}=\frac{1}{3}B_1C_1\cdot S_{\triangle C_1CE}=\frac{1}{3}\times1\times\frac{1}{2}\times1\times1=\frac{1}{6}$,故C错误;
对于D,由题意易知,$\overrightarrow{AD}=(0,1,0)$为平面$CDD_1C_1$的一个法向量,$\overrightarrow{B_1E}=(-1,1,-\frac{1}{2})$,设直线$B_1E$与平面$CDD_1C_1$所成的角为$\theta$,所以$\sin\theta=\frac{\vert\overrightarrow{B_1E}\cdot\overrightarrow{AD}\vert}{\vert\overrightarrow{B_1E}\vert\vert\overrightarrow{AD}\vert}=\frac{1}{\frac{3}{2}\times1}=\frac{2}{3}$,所以$\theta\neq60^{\circ}$,故D错误.故选AB.
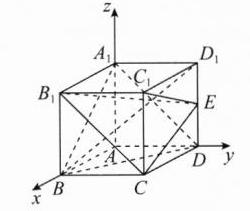
9.AB【解析】如图,建立空间直角坐标系,则$A(0,0,0),B(1,0,0),C(1,1,0),D(0,1,0),A_1(0,0,1),B_1(1,0,1),C_1(1,1,1),D_1(0,1,1),E(0,1,\frac{1}{2})$,所以$\overrightarrow{B_1C}=(0,1,-1),\overrightarrow{BD_1}=(-1,1,1),\overrightarrow{BD}=(-1,1,0),\overrightarrow{BA_1}=(-1,0,1)$.
对于A,设平面$A_1BD$的法向量为$\boldsymbol{n}=(x,y,z)$,则$\begin{cases}\boldsymbol{n}\cdot\overrightarrow{BA_1}=0\\\boldsymbol{n}\cdot\overrightarrow{BD}=0\end{cases}$,即$\begin{cases}-x + z = 0\\-x + y = 0\end{cases}$,取$\boldsymbol{n}=(1,1,1)$,
则$\boldsymbol{n}\cdot\overrightarrow{B_1C}=1\times0 + 1\times1 + 1\times(-1)=0$,即$\boldsymbol{n}\perp\overrightarrow{B_1C}$,又直线$B_1C\not\subset$平面$A_1BD$,所以直线$B_1C//$平面$A_1BD$,故A正确;
对于B,因为$\overrightarrow{B_1C}\cdot\overrightarrow{BD_1}=0\times(-1)+1\times1+(-1)\times1 = 0$,所以$\overrightarrow{B_1C}\perp\overrightarrow{BD_1}$,即$B_1C\perp BD_1$,故B正确;
对于C,$V_{C_1 - B_1CE}=V_{B_1 - C_1CE}=\frac{1}{3}B_1C_1\cdot S_{\triangle C_1CE}=\frac{1}{3}\times1\times\frac{1}{2}\times1\times1=\frac{1}{6}$,故C错误;
对于D,由题意易知,$\overrightarrow{AD}=(0,1,0)$为平面$CDD_1C_1$的一个法向量,$\overrightarrow{B_1E}=(-1,1,-\frac{1}{2})$,设直线$B_1E$与平面$CDD_1C_1$所成的角为$\theta$,所以$\sin\theta=\frac{\vert\overrightarrow{B_1E}\cdot\overrightarrow{AD}\vert}{\vert\overrightarrow{B_1E}\vert\vert\overrightarrow{AD}\vert}=\frac{1}{\frac{3}{2}\times1}=\frac{2}{3}$,所以$\theta\neq60^{\circ}$,故D错误.故选AB.

10. [广东广州四中2024高二月考]在长方体ABCD - A₁B₁C₁D₁中,AB = 2AD = 2AA₁ = 2,动点P满足$\overrightarrow{A_{1}P}=x\overrightarrow{A_{1}D_{1}}+y\overrightarrow{A_{1}A}+z\overrightarrow{A_{1}B_{1}}$,$x\in(0,1]$,$y\in(0,1]$,$z\in(0,1]$,则下列结论正确的有 ( )
A. 当x = y = z时,A₁P⊥BD
B. 当x + y + z = 1时,D₁P//平面BDC₁
C. 当x = y = 1,$z=\frac{1}{2}$时,点P到直线AB₁的距离为$\frac{\sqrt{30}}{5}$
D. 当x = y = z=$\frac{1}{3}$时,点P为△AB₁D₁的重心
A. 当x = y = z时,A₁P⊥BD
B. 当x + y + z = 1时,D₁P//平面BDC₁
C. 当x = y = 1,$z=\frac{1}{2}$时,点P到直线AB₁的距离为$\frac{\sqrt{30}}{5}$
D. 当x = y = z=$\frac{1}{3}$时,点P为△AB₁D₁的重心
答案:
10.BCD【解析】以$D$为坐标原点,$\overrightarrow{DA},\overrightarrow{DC},\overrightarrow{DD_1}$的方向分别为$x,y,z$轴的正方向,建立如图所示的空间直角坐标系,

则$A(1,0,0),B(1,2,0),C(0,2,0),D(0,0,0),A_1(1,0,1),B_1(1,2,1),C_1(0,2,1),D_1(0,0,1)$,
可得$\overrightarrow{A_1D_1}=(-1,0,0),\overrightarrow{A_1A}=(0,0,-1),\overrightarrow{A_1B_1}=(0,2,0)$.
对于选项A:设$x = y = z = a\in(0,1]$,则$\overrightarrow{A_1P}=a\overrightarrow{A_1D_1}+a\overrightarrow{A_1A}+a\overrightarrow{A_1B_1}=(-a,2a,-a)$,
因为$\overrightarrow{BD}=(-1,-2,0)$,所以$\overrightarrow{A_1P}\cdot\overrightarrow{BD}=a - 4a=-3a$,不为$0$,
所以$A_1P\perp BD$不成立,故A错误;
对于选项B:由$\overrightarrow{B_1D_1}=\overrightarrow{BD}=(-1,-2,0)$,可知$B_1D_1// BD$,
$BD\subset$平面$BDC_1$,$B_1D_1\not\subset$平面$BDC_1$,所以$B_1D_1//$平面$BDC_1$,
同理可得,$AD_1//$平面$BDC_1$,
又$AD_1\cap B_1D_1 = D_1$,$AD_1,B_1D_1\subset$平面$AB_1D_1$,
所以平面$AB_1D_1//$平面$BDC_1$,
当$x + y + z = 1$时,$A,B_1,D_1,P$四点共面,即$D_1P\subset$平面$AB_1D_1$,
所以$D_1P//$平面$BDC_1$,故B正确;
对于选项C:当$x = y = 1,z = \frac{1}{2}$时,
$\overrightarrow{A_1P}=\overrightarrow{A_1D_1}+\overrightarrow{A_1A}+\frac{1}{2}\overrightarrow{A_1B_1}=(-1,1,-1),\overrightarrow{AA_1}=(0,0,1)$,可得$\overrightarrow{AP}=\overrightarrow{AA_1}+\overrightarrow{A_1P}=(-1,1,0)$,又$\overrightarrow{AB_1}=(0,2,1)$,所以点$P$到直线$AB_1$的距离为$\sqrt{\vert\overrightarrow{AP}\vert^2-(\frac{\vert\overrightarrow{AP}\cdot\overrightarrow{AB_1}\vert}{\vert\overrightarrow{AB_1}\vert})^2}=\frac{\sqrt{30}}{5}$,故C正确;
对于选项D:当$x = y = z = \frac{1}{3}$时,$\overrightarrow{A_1P}=\frac{1}{3}\overrightarrow{A_1D_1}+\frac{1}{3}\overrightarrow{A_1A}+\frac{1}{3}\overrightarrow{A_1B_1}=(-\frac{1}{3},\frac{2}{3},-\frac{1}{3})$,
且$A_1(1,0,1)$,可知$P(\frac{2}{3},\frac{2}{3},\frac{2}{3})$,
由$A(1,0,0),B_1(1,2,1),D_1(0,0,1)$可知,$\triangle AB_1D_1$的重心为$(\frac{2}{3},\frac{2}{3},\frac{2}{3})$,所以点$P$为$\triangle AB_1D_1$的重心,故D正确.
故选BCD.
10.BCD【解析】以$D$为坐标原点,$\overrightarrow{DA},\overrightarrow{DC},\overrightarrow{DD_1}$的方向分别为$x,y,z$轴的正方向,建立如图所示的空间直角坐标系,

则$A(1,0,0),B(1,2,0),C(0,2,0),D(0,0,0),A_1(1,0,1),B_1(1,2,1),C_1(0,2,1),D_1(0,0,1)$,
可得$\overrightarrow{A_1D_1}=(-1,0,0),\overrightarrow{A_1A}=(0,0,-1),\overrightarrow{A_1B_1}=(0,2,0)$.
对于选项A:设$x = y = z = a\in(0,1]$,则$\overrightarrow{A_1P}=a\overrightarrow{A_1D_1}+a\overrightarrow{A_1A}+a\overrightarrow{A_1B_1}=(-a,2a,-a)$,
因为$\overrightarrow{BD}=(-1,-2,0)$,所以$\overrightarrow{A_1P}\cdot\overrightarrow{BD}=a - 4a=-3a$,不为$0$,
所以$A_1P\perp BD$不成立,故A错误;
对于选项B:由$\overrightarrow{B_1D_1}=\overrightarrow{BD}=(-1,-2,0)$,可知$B_1D_1// BD$,
$BD\subset$平面$BDC_1$,$B_1D_1\not\subset$平面$BDC_1$,所以$B_1D_1//$平面$BDC_1$,
同理可得,$AD_1//$平面$BDC_1$,
又$AD_1\cap B_1D_1 = D_1$,$AD_1,B_1D_1\subset$平面$AB_1D_1$,
所以平面$AB_1D_1//$平面$BDC_1$,
当$x + y + z = 1$时,$A,B_1,D_1,P$四点共面,即$D_1P\subset$平面$AB_1D_1$,
所以$D_1P//$平面$BDC_1$,故B正确;
对于选项C:当$x = y = 1,z = \frac{1}{2}$时,
$\overrightarrow{A_1P}=\overrightarrow{A_1D_1}+\overrightarrow{A_1A}+\frac{1}{2}\overrightarrow{A_1B_1}=(-1,1,-1),\overrightarrow{AA_1}=(0,0,1)$,可得$\overrightarrow{AP}=\overrightarrow{AA_1}+\overrightarrow{A_1P}=(-1,1,0)$,又$\overrightarrow{AB_1}=(0,2,1)$,所以点$P$到直线$AB_1$的距离为$\sqrt{\vert\overrightarrow{AP}\vert^2-(\frac{\vert\overrightarrow{AP}\cdot\overrightarrow{AB_1}\vert}{\vert\overrightarrow{AB_1}\vert})^2}=\frac{\sqrt{30}}{5}$,故C正确;
对于选项D:当$x = y = z = \frac{1}{3}$时,$\overrightarrow{A_1P}=\frac{1}{3}\overrightarrow{A_1D_1}+\frac{1}{3}\overrightarrow{A_1A}+\frac{1}{3}\overrightarrow{A_1B_1}=(-\frac{1}{3},\frac{2}{3},-\frac{1}{3})$,
且$A_1(1,0,1)$,可知$P(\frac{2}{3},\frac{2}{3},\frac{2}{3})$,
由$A(1,0,0),B_1(1,2,1),D_1(0,0,1)$可知,$\triangle AB_1D_1$的重心为$(\frac{2}{3},\frac{2}{3},\frac{2}{3})$,所以点$P$为$\triangle AB_1D_1$的重心,故D正确.
故选BCD.
11. [陕西西安中学2024高二期中]如图,在菱形ABCD中,$AB=\frac{4\sqrt{3}}{3}$,∠BAD = 60°,沿对角线BD将△ABD折起,使点A,C之间的距离为$2\sqrt{2}$.若P,Q分别为线段BD,CA上的动点,则下列说法正确的是 ( )

A. 平面ABD⊥平面BCD
B. 线段PQ长度的最小值为$\sqrt{2}$
C. 当AQ = QC,4PD = DB时,点D到直线PQ的距离为$\frac{\sqrt{14}}{14}$
D. 当P,Q分别为线段BD,CA的中点时,PQ与AD所成角的余弦值为$\frac{\sqrt{6}}{4}$

A. 平面ABD⊥平面BCD
B. 线段PQ长度的最小值为$\sqrt{2}$
C. 当AQ = QC,4PD = DB时,点D到直线PQ的距离为$\frac{\sqrt{14}}{14}$
D. 当P,Q分别为线段BD,CA的中点时,PQ与AD所成角的余弦值为$\frac{\sqrt{6}}{4}$
答案:
11.ABD【解析】取$BD$的中点$O$,连接$OA,OC$.在菱形$ABCD$中,$AB=\frac{4\sqrt{3}}{3},\angle BAD = 60^{\circ}$,所以$OA = OC = AB\sin60^{\circ}=\frac{4\sqrt{3}}{3}\times\frac{\sqrt{3}}{2}=2$.
因为$AC = 2\sqrt{2}$,所以$OA^2 + OC^2 = AC^2$,所以$OA\perp OC$.
又因为$AB = AD$,$O$为$BD$的中点,所以$OA\perp BD$,同理可得$OC\perp BD$,
因为$OA\perp OC,OA\perp BD,OC\cap BD = O,OC,BD\subset$平面$BCD$,
所以$OA\perp$平面$BCD$.
因为$OA\subset$平面$ABD$,所以平面$ABD\perp$平面$BCD$,故A正确.
又$OA\perp BD,OA\perp OC,OC\perp BD$,
故以$O$为原点,$OB,OC,OA$所在直线分别为$x,y,z$轴建立如图所示的空间直角坐标系,

则$B(\frac{2\sqrt{3}}{3},0,0),C(0,2,0),A(0,0,2),D(-\frac{2\sqrt{3}}{3},0,0)$.
当$AQ = QC,4PD = DB$时,$Q(0,1,1),P(-\frac{\sqrt{3}}{3},0,0)$,
$\overrightarrow{PQ}=(\frac{\sqrt{3}}{3},1,1),\overrightarrow{DP}=(\frac{\sqrt{3}}{3},0,0)$,
所以点$D$到直线$PQ$的距离为$\sqrt{\vert\overrightarrow{DP}\vert^2-(\frac{\vert\overrightarrow{PQ}\cdot\overrightarrow{DP}\vert}{\vert\overrightarrow{PQ}\vert})^2}=\sqrt{\frac{1}{3}-(\frac{\frac{1}{3}}{\frac{\sqrt{21}}{3}})^2}=\frac{\sqrt{14}}{7}$,故C错误.
设$P(a,0,0)(-\frac{2\sqrt{3}}{3}\leq a\leq\frac{2\sqrt{3}}{3})$,$Q(x,y,z)$,设$\overrightarrow{CQ}=\lambda\overrightarrow{CA},\lambda\in[0,1]$,得$Q(0,2 - 2\lambda,2\lambda)$,
$\vert PQ\vert=\sqrt{(-a)^2+(2 - 2\lambda)^2+(2\lambda)^2}=\sqrt{a^2 + 8(\lambda - \frac{1}{2})^2+2}$,
当$a = 0$且$\lambda=\frac{1}{2}$时,$\vert PQ\vert_{min}=\sqrt{2}$,故B正确.
当$P,Q$分别为线段$BD,CA$的中点时,$P(0,0,0),Q(0,1,1)$,
$\overrightarrow{PQ}=(0,1,1),\overrightarrow{AD}=(-\frac{2\sqrt{3}}{3},0,-2)$,
设$PQ$与$AD$所成的角为$\theta$,则$\cos\theta=\frac{\vert\overrightarrow{PQ}\cdot\overrightarrow{AD}\vert}{\vert\overrightarrow{PQ}\vert\vert\overrightarrow{AD}\vert}=\frac{2}{\sqrt{2}\times\sqrt{\frac{16}{3}}}=\frac{\sqrt{6}}{4}$,
所以$PQ$与$AD$所成角的余弦值为$\frac{\sqrt{6}}{4}$,故D正确.故选ABD.
11.ABD【解析】取$BD$的中点$O$,连接$OA,OC$.在菱形$ABCD$中,$AB=\frac{4\sqrt{3}}{3},\angle BAD = 60^{\circ}$,所以$OA = OC = AB\sin60^{\circ}=\frac{4\sqrt{3}}{3}\times\frac{\sqrt{3}}{2}=2$.
因为$AC = 2\sqrt{2}$,所以$OA^2 + OC^2 = AC^2$,所以$OA\perp OC$.
又因为$AB = AD$,$O$为$BD$的中点,所以$OA\perp BD$,同理可得$OC\perp BD$,
因为$OA\perp OC,OA\perp BD,OC\cap BD = O,OC,BD\subset$平面$BCD$,
所以$OA\perp$平面$BCD$.
因为$OA\subset$平面$ABD$,所以平面$ABD\perp$平面$BCD$,故A正确.
又$OA\perp BD,OA\perp OC,OC\perp BD$,
故以$O$为原点,$OB,OC,OA$所在直线分别为$x,y,z$轴建立如图所示的空间直角坐标系,

则$B(\frac{2\sqrt{3}}{3},0,0),C(0,2,0),A(0,0,2),D(-\frac{2\sqrt{3}}{3},0,0)$.
当$AQ = QC,4PD = DB$时,$Q(0,1,1),P(-\frac{\sqrt{3}}{3},0,0)$,
$\overrightarrow{PQ}=(\frac{\sqrt{3}}{3},1,1),\overrightarrow{DP}=(\frac{\sqrt{3}}{3},0,0)$,
所以点$D$到直线$PQ$的距离为$\sqrt{\vert\overrightarrow{DP}\vert^2-(\frac{\vert\overrightarrow{PQ}\cdot\overrightarrow{DP}\vert}{\vert\overrightarrow{PQ}\vert})^2}=\sqrt{\frac{1}{3}-(\frac{\frac{1}{3}}{\frac{\sqrt{21}}{3}})^2}=\frac{\sqrt{14}}{7}$,故C错误.
设$P(a,0,0)(-\frac{2\sqrt{3}}{3}\leq a\leq\frac{2\sqrt{3}}{3})$,$Q(x,y,z)$,设$\overrightarrow{CQ}=\lambda\overrightarrow{CA},\lambda\in[0,1]$,得$Q(0,2 - 2\lambda,2\lambda)$,
$\vert PQ\vert=\sqrt{(-a)^2+(2 - 2\lambda)^2+(2\lambda)^2}=\sqrt{a^2 + 8(\lambda - \frac{1}{2})^2+2}$,
当$a = 0$且$\lambda=\frac{1}{2}$时,$\vert PQ\vert_{min}=\sqrt{2}$,故B正确.
当$P,Q$分别为线段$BD,CA$的中点时,$P(0,0,0),Q(0,1,1)$,
$\overrightarrow{PQ}=(0,1,1),\overrightarrow{AD}=(-\frac{2\sqrt{3}}{3},0,-2)$,
设$PQ$与$AD$所成的角为$\theta$,则$\cos\theta=\frac{\vert\overrightarrow{PQ}\cdot\overrightarrow{AD}\vert}{\vert\overrightarrow{PQ}\vert\vert\overrightarrow{AD}\vert}=\frac{2}{\sqrt{2}\times\sqrt{\frac{16}{3}}}=\frac{\sqrt{6}}{4}$,
所以$PQ$与$AD$所成角的余弦值为$\frac{\sqrt{6}}{4}$,故D正确.故选ABD.
12. 已知空间向量a = (-1,2,4),b = (1,-4,2),c = (x,4,z).
(1)若(a + 2b)⊥c,且x = 4,则z =________;
(2)若a,b,c共面,在以下三个条件①x = 1,②x = 0,③x = -2中选取一个作为已知,则z的值可以为________.(答对一空给3分)
(1)若(a + 2b)⊥c,且x = 4,则z =________;
(2)若a,b,c共面,在以下三个条件①x = 1,②x = 0,③x = -2中选取一个作为已知,则z的值可以为________.(答对一空给3分)
答案:
12.
(1)$\frac{5}{2}$
(2)$-22$或$-12$或$8$(只需写出一个)【解析】
(1)当$x = 4$时,$\boldsymbol{c}=(4,4,z)$.
因为$\boldsymbol{a}=(-1,2,4),\boldsymbol{b}=(1,-4,2)$,所以$\boldsymbol{a}+2\boldsymbol{b}=(1,-6,8)$.
因为$(\boldsymbol{a}+2\boldsymbol{b})\perp\boldsymbol{c}$,所以$(\boldsymbol{a}+2\boldsymbol{b})\cdot\boldsymbol{c}=1\times4 - 6\times4 + 8z = 0$,解得$z = \frac{5}{2}$.
(2)因为$\boldsymbol{a},\boldsymbol{b},\boldsymbol{c}$共面,所以由空间向量基本定理可知,$\boldsymbol{c}=\lambda\boldsymbol{a}+\mu\boldsymbol{b},\lambda,\mu\in\mathbf{R}$.
选①$x = 1$,则$(1,4,z)=(-\lambda,2\lambda,4\lambda)+(\mu,-4\mu,2\mu)=(-\lambda+\mu,2\lambda - 4\mu,4\lambda + 2\mu)$,故$\begin{cases}-\lambda+\mu = 1\\2\lambda - 4\mu = 4\\4\lambda + 2\mu = z\end{cases}$,解得$z = - 22$.
选②$x = 0$,则$(0,4,z)=(-\lambda,2\lambda,4\lambda)+(\mu,-4\mu,2\mu)=(-\lambda+\mu,2\lambda - 4\mu,4\lambda + 2\mu)$,
故$\begin{cases}-\lambda+\mu = 0\\2\lambda - 4\mu = 4\\4\lambda + 2\mu = z\end{cases}$,解得$z = - 12$.
选③$x = - 2$,则$(-2,4,z)=(-\lambda,2\lambda,4\lambda)+(\mu,-4\mu,2\mu)=(-\lambda+\mu,2\lambda - 4\mu,4\lambda + 2\mu)$,
故$\begin{cases}-\lambda+\mu = - 2\\2\lambda - 4\mu = 4\\4\lambda + 2\mu = z\end{cases}$,解得$z = 8$.
综上所述,$z$的值可以为$-22$或$-12$或$8$.
(1)$\frac{5}{2}$
(2)$-22$或$-12$或$8$(只需写出一个)【解析】
(1)当$x = 4$时,$\boldsymbol{c}=(4,4,z)$.
因为$\boldsymbol{a}=(-1,2,4),\boldsymbol{b}=(1,-4,2)$,所以$\boldsymbol{a}+2\boldsymbol{b}=(1,-6,8)$.
因为$(\boldsymbol{a}+2\boldsymbol{b})\perp\boldsymbol{c}$,所以$(\boldsymbol{a}+2\boldsymbol{b})\cdot\boldsymbol{c}=1\times4 - 6\times4 + 8z = 0$,解得$z = \frac{5}{2}$.
(2)因为$\boldsymbol{a},\boldsymbol{b},\boldsymbol{c}$共面,所以由空间向量基本定理可知,$\boldsymbol{c}=\lambda\boldsymbol{a}+\mu\boldsymbol{b},\lambda,\mu\in\mathbf{R}$.
选①$x = 1$,则$(1,4,z)=(-\lambda,2\lambda,4\lambda)+(\mu,-4\mu,2\mu)=(-\lambda+\mu,2\lambda - 4\mu,4\lambda + 2\mu)$,故$\begin{cases}-\lambda+\mu = 1\\2\lambda - 4\mu = 4\\4\lambda + 2\mu = z\end{cases}$,解得$z = - 22$.
选②$x = 0$,则$(0,4,z)=(-\lambda,2\lambda,4\lambda)+(\mu,-4\mu,2\mu)=(-\lambda+\mu,2\lambda - 4\mu,4\lambda + 2\mu)$,
故$\begin{cases}-\lambda+\mu = 0\\2\lambda - 4\mu = 4\\4\lambda + 2\mu = z\end{cases}$,解得$z = - 12$.
选③$x = - 2$,则$(-2,4,z)=(-\lambda,2\lambda,4\lambda)+(\mu,-4\mu,2\mu)=(-\lambda+\mu,2\lambda - 4\mu,4\lambda + 2\mu)$,
故$\begin{cases}-\lambda+\mu = - 2\\2\lambda - 4\mu = 4\\4\lambda + 2\mu = z\end{cases}$,解得$z = 8$.
综上所述,$z$的值可以为$-22$或$-12$或$8$.
13. [河南驻马店高级中学2024高二月考]已知圆锥PO(P为圆锥顶点,O为底面圆心)的轴截面是边长为2的等边三角形,A,B,C为底面圆周上三点,若空间一动点Q满足$\overrightarrow{PQ}=2x\overrightarrow{PA}+y\overrightarrow{PB}+(1 - 2x - y)\overrightarrow{PC}$,则|$\overrightarrow{PQ}$|的最小值为________.
答案:
13.$\sqrt{3}$【解析】因为$\overrightarrow{PQ}=2x\overrightarrow{PA}+y\overrightarrow{PB}+(1 - 2x - y)\overrightarrow{PC}$,
所以$\overrightarrow{PQ}-\overrightarrow{PC}=2x\overrightarrow{PA}-2x\overrightarrow{PC}+y\overrightarrow{PB}-y\overrightarrow{PC}$,即$\overrightarrow{CQ}=2x\overrightarrow{CA}+y\overrightarrow{CB}$,
所以$\overrightarrow{CQ},\overrightarrow{CA},\overrightarrow{CB}$共面.
又$A,B,C$为底面圆周上三点,所以点$Q$为平面$ABC$上一点.
由题意知$PO\perp$平面$ABC$,
所以$\vert\overrightarrow{PQ}\vert\geq\vert\overrightarrow{PO}\vert$,又圆锥$PO$的轴截面是边长为$2$的等边三角形,所以$\vert\overrightarrow{PO}\vert=\sqrt{3}$,所以$\vert\overrightarrow{PQ}\vert$的最小值为$\sqrt{3}$.
所以$\overrightarrow{PQ}-\overrightarrow{PC}=2x\overrightarrow{PA}-2x\overrightarrow{PC}+y\overrightarrow{PB}-y\overrightarrow{PC}$,即$\overrightarrow{CQ}=2x\overrightarrow{CA}+y\overrightarrow{CB}$,
所以$\overrightarrow{CQ},\overrightarrow{CA},\overrightarrow{CB}$共面.
又$A,B,C$为底面圆周上三点,所以点$Q$为平面$ABC$上一点.
由题意知$PO\perp$平面$ABC$,
所以$\vert\overrightarrow{PQ}\vert\geq\vert\overrightarrow{PO}\vert$,又圆锥$PO$的轴截面是边长为$2$的等边三角形,所以$\vert\overrightarrow{PO}\vert=\sqrt{3}$,所以$\vert\overrightarrow{PQ}\vert$的最小值为$\sqrt{3}$.
14. [河北保定2024高二月考]半正多面体亦称“阿基米德多面体”,是由边数不全相同的正多边形围成的多面体,体现了数学的对称美.二十四等边体就是一种半正多面体,是由正方体切截而成的,它由八个正三角形和六个正方形构成(如图所示).若它的所有棱长都为$\sqrt{2}$,则以下结论正确的是________.(填序号)
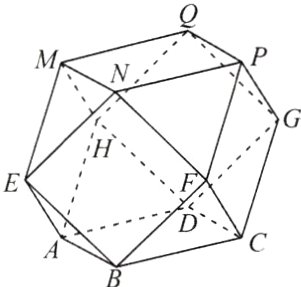
①BF⊥平面EAB;
②该二十四等边体的体积为$\frac{20}{3}$;
③该二十四等边体外接球的表面积为8π;
④PN与平面EBFN所成角的正弦值为$\frac{\sqrt{2}}{2}$.

①BF⊥平面EAB;
②该二十四等边体的体积为$\frac{20}{3}$;
③该二十四等边体外接球的表面积为8π;
④PN与平面EBFN所成角的正弦值为$\frac{\sqrt{2}}{2}$.
答案:
14.②③④【解析】将几何体补成正方体$ORLI - O_1R_1L_1I_1$,
以点$O$为坐标原点,$OR,OI,OO_1$所在直线分别为$x,y,z$轴建立如图所示的空间直角坐标系.
对于①,$A(1,0,0),B(2,1,0),E(2,0,1),F(2,2,1)$,
所以$\overrightarrow{BF}=(0,1,1),\overrightarrow{AB}=(1,1,0)$,则$\overrightarrow{BF}\cdot\overrightarrow{AB}\neq0$,故①错误;
对于②,该二十四等边体是在正方体$ORLI - O_1R_1L_1I_1$上截去$8$个全等的三棱锥而成,
且三棱锥的底面是腰长为$1$的等腰直角三角形,三棱锥的高为$1$,
故该二十四等边体的体积$V = 2^3-8\times\frac{1}{3}\times1\times\frac{1}{2}\times1^2=\frac{20}{3}$,故②正确;
对于③,易知正方体$ORLI - O_1R_1L_1I_1$的中心$X(1,1,1)$为该二十四等边体外接球的球心,且该球的半径为$XA=\sqrt{0 + 1^2+1^2}=\sqrt{2}$,
因此,该二十四等边体外接球的表面积为$4\pi(\sqrt{2})^2 = 8\pi$,故③正确;
对于④,易知平面$EBFN$的一个法向量为$\boldsymbol{n}=(1,0,0),P(1,2,2),N(2,1,2)$,所以$\overrightarrow{PN}=(1,-1,0)$,
所以$\cos\langle\boldsymbol{n},\overrightarrow{PN}\rangle=\frac{\boldsymbol{n}\cdot\overrightarrow{PN}}{\vert\boldsymbol{n}\vert\vert\overrightarrow{PN}\vert}=\frac{1}{1\times\sqrt{2}}=\frac{\sqrt{2}}{2}$,故$PN$与平面$EBFN$所成角的正弦值为$\frac{\sqrt{2}}{2}$,故④正确.
故答案为②③④.
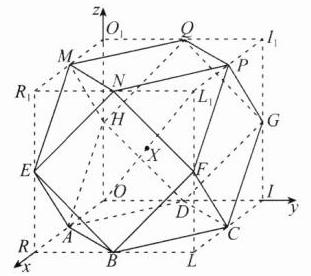
14.②③④【解析】将几何体补成正方体$ORLI - O_1R_1L_1I_1$,
以点$O$为坐标原点,$OR,OI,OO_1$所在直线分别为$x,y,z$轴建立如图所示的空间直角坐标系.
对于①,$A(1,0,0),B(2,1,0),E(2,0,1),F(2,2,1)$,
所以$\overrightarrow{BF}=(0,1,1),\overrightarrow{AB}=(1,1,0)$,则$\overrightarrow{BF}\cdot\overrightarrow{AB}\neq0$,故①错误;
对于②,该二十四等边体是在正方体$ORLI - O_1R_1L_1I_1$上截去$8$个全等的三棱锥而成,
且三棱锥的底面是腰长为$1$的等腰直角三角形,三棱锥的高为$1$,
故该二十四等边体的体积$V = 2^3-8\times\frac{1}{3}\times1\times\frac{1}{2}\times1^2=\frac{20}{3}$,故②正确;
对于③,易知正方体$ORLI - O_1R_1L_1I_1$的中心$X(1,1,1)$为该二十四等边体外接球的球心,且该球的半径为$XA=\sqrt{0 + 1^2+1^2}=\sqrt{2}$,
因此,该二十四等边体外接球的表面积为$4\pi(\sqrt{2})^2 = 8\pi$,故③正确;
对于④,易知平面$EBFN$的一个法向量为$\boldsymbol{n}=(1,0,0),P(1,2,2),N(2,1,2)$,所以$\overrightarrow{PN}=(1,-1,0)$,
所以$\cos\langle\boldsymbol{n},\overrightarrow{PN}\rangle=\frac{\boldsymbol{n}\cdot\overrightarrow{PN}}{\vert\boldsymbol{n}\vert\vert\overrightarrow{PN}\vert}=\frac{1}{1\times\sqrt{2}}=\frac{\sqrt{2}}{2}$,故$PN$与平面$EBFN$所成角的正弦值为$\frac{\sqrt{2}}{2}$,故④正确.
故答案为②③④.

查看更多完整答案,请扫码查看


