《2025年零失误分层训练高中数学必修第二册人教版黑吉辽内蒙古专版》

1.(2024·福建福州山海联盟协作体高一下期末)已知一组数据为20,30,40,50,50,60,70,80,其平均数、第60百分位数和众数的大小关系是
(D)

A.平均数＞第60百分位数＞众数
B.平均数＜第60百分位数＜众数
C.第60百分位数＜众数＜平均数
D.平均数=第60百分位数=众数

答案： 1.D[提示：从小到大排列数据为20,30,40,50,50,60,70,80，其中，50出现了2次，为出现次数最多的数，故众数为50；共8个数据，故第60百分位数为第5个数50,平均数=(20+30+40+50+50+60+70+80)÷8=50.
∴众数=第60百分位数=平均数.]

2.(2025·河北沧州市四校联考高一下期末) [多选]某科研院所共有科研人员200人,统计得到如下数据：

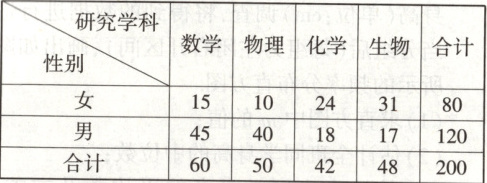
欲了解该所科研人员的创新能力,决定抽取40名科研人员进行调查,下列说法正确的是
(AD)

A.若按照研究学科进行分层抽样(按比例分配),则数学学科科研人员一定被抽取12人
B.若按照性别进行分层抽样(按比例分配),则男性科研人员可能被抽取20人
C.若按照简单随机抽样,则女性科研人员一定被抽取10人
D.若按照简单随机抽样,则可能抽出的均为数学学科科研人员

答案： 2.AD[提示：对于A,因为按照研究学科进行分层抽样(按比例分配)，所以数学学科科研人员一定被抽取$40×\frac{60}{200}=12（$人），故A正确；对于B,因为按照性别进行分层抽样(按比例分配)，所以男性科研人员被抽取$40×\frac{120}{200}=24($人)，故B错误；对于C,若按照简单随机抽样，则女性科研人员不一定被抽取10人，故C错误；对于D,若按照简单随机抽样，则可能抽出的均为数学学科科研人员，故D正确.]

3.(2025·安徽合肥中国科学技术大学附中高一下期末)[多选]2025年亚洲冬季运动会于2025年2月7日至2月14日在黑龙江哈尔滨市举行,中国队获得32枚金牌,27枚银牌,26枚铜牌,共85枚奖牌,排名第一.如图是中国队2月8日至2月12日的奖牌数的统计图,关于这5个比赛日的统计数据,下列说法正确的是
(ABD)

A.金牌数的方差是1.76
B.铜牌数的极差是8
C.银牌数的众数是3
D.日奖牌总数的第50%分位数是16

答案： 3.ABD[提示：对于A,由折线图得这5个比赛日中国队获得金牌数的平均值为$\frac{8+7+6+6+4}{5}=6.2，$方差$s^{2}=\frac{1}{5}×[(8-6.2)^{2}+(7-6.2)^{2}+(6-6.2)^{2}+(6-6.2)^{2}+(4-6.2)^{2}]=1.76，$故A正确.对于B,这5个比赛日中国队获得铜牌数最多的是2月9日的9枚，最少的是2月10日的1枚，铜牌数的极差为9-1=8，故B正确.对于C,这5个比赛日中国队获得银牌数的众数为3和8，故C错误.对于D,将这5个比赛日中国队的日奖牌总数按从小到大的顺序排列，依次为9,10,16,21,24，
∵5×50%=2.5，
∴日奖牌总数的第50%分位数是16，故D正确.]

4.(2025·广东广州越秀区高一下期末)[多选]某校为了解高一年级学生的身高情况,采用样本量按比例分配的分层随机抽样,抽取了男生20人,其平均数和方差分别为172和12;抽取了女生30人,其平均数和方差分别为162和24.由这些数据,可计算出总样本平均数$\overline{x}$与总样本方差$s^2$分别是(AD)

A.$\overline{x}=166$
B.$\overline{x}=167$
C.$s^2=19.2$
D.$s^2=43.2$

答案： 4.AD[提示：根据题意可得总样本平均数为$\bar{x}=\frac{20×172+30×162}{20+30}=166,$总样本方差为$s^{2}=\frac{20}{20+30}×[12+(172-166)^{2}]+\frac{30}{20+30}×[24+(162-166)^{2}]=43.2.]$

5.(2025·广东广州三校高一下期末)[多选]下列说法正确的是 (ABD)

A.用简单随机抽样的方法从含有50个个体的总体中抽取一个容量为5的样本,则个体$m$被抽到的概率是0.1
B.数据$x_1,x_2,·s,x_{10}$的平均数为90,方差为3,数据$y_1,y_2,·s,y_{15}$的平均数为85,方差为5,则$x_1,x_2,·s,x_{10},y_1,y_2,·s,y_{15}$的平均数为87,方差为10.2
C.已知数据$x_1,x_2,·s,x_{10}$的极差为6,方差为2,则数据$2x_1+1,2x_2+1,·s,2x_{10}+1$的极差和方差分别为12,9
D.数据13,27,24,12,14,30,15,17,19,23的上四分位数是24

答案： 5.ABD[提示：对于A,简单随机抽样中，个体被抽取的概率等于样本容量与总体容量之比，总体有50个个体，抽取容量为5的样本，所以个体m被抽到的概率为$\frac{5}{50}=0.1，$故A正确；对于B,混合数据的平均数为$\frac{10×90+15×85}{10+15}=87，$方差为$\frac{10}{10+15}×[3^{2}+(90-87)^{2}]+\frac{15}{10+15}×[5^{2}+(85-87)^{2}]=10.2，$故B正确；对于C,设原数据的最大值为M、最小值为m，则极差M-m=6，方差$s^{2}=2，$新数据$2x_{i}+1(i=1,2,⋯,10)，$极差为(2M+1)-(2m+1)=2(M-m)=12，方差为$2^{2}×s^{2}=4×2=8，$故C错误；对于D,把数据按从小到大排序：12,13,14,15，17,19,23,24,27,30，上四分位数对应75%位置，10×75%=7.5，向上取整为第8个数，即24，故D正确.]

6.(2025·安徽合肥168中学高一下期末)一家水果店的店长为了解本店水果的日销售情况,记录了过去30天苹果的日销售量(单位：kg),结果如下：83,96,107,91,70,75,94,80,80,100,75,99,117,89,74,94,84,85,101,87,93,85,107,99,55,97,86,84,85,104.
一次进货太多,水果会变得不新鲜；进货太少,又不能满足顾客的需求.店长希望每天的苹果尽量新鲜,又能满足80%的顾客的需求(在100天中,大约有80天可以满足顾客的需求),则每天应该进99.5千克的苹果.

答案： 6.99.5[提示：过去30天苹果的日销售量按从低到高排列为55,70,74,75,75,80,80,83,84,84,85,85,85,86,87,89,91，93,94,94,96,97,99,99,100,101,104,107,107,117.
∵30×80%=24，
∴第80百分位数为$\frac{99+100}{2}=99.5.]$