《2025年零失误分层训练高中数学必修第二册人教版黑吉辽内蒙古专版》

1. (2025·黑龙江牡丹江市名校协作体月考)已知平面内的向量$\boldsymbol{a}$在向量$\boldsymbol{b}$上的投影向量为$\frac{1}{2}\boldsymbol{b}$,且$|\boldsymbol{a}| = |\boldsymbol{b}| = 1$,则$|\boldsymbol{a} - 2\boldsymbol{b}|$的值为(A)

A.$\sqrt{3}$
B.1
C.$\frac{3}{4}$
D.$\frac{\sqrt{3}}{2}$

答案： 1.A[提示：$\because$平面内的向量$a$在向量$b$上的投影向量为$\frac{1}{2}b$，$|b|=1$，$\therefore\frac{a· b}{|b|}=\frac{b}{|b|}·\frac{1}{2}b$，解得$a· b=\frac{1}{2}$，故$|a - 2b|=\sqrt{a^{2}-4a· b + 4b^{2}}=\sqrt{1 - 4×\frac{1}{2}+4}=\sqrt{3}$.]

2. (2025·黑龙江哈尔滨九中高一下月考)已知$\boldsymbol{a}$,$\boldsymbol{b}$均为单位向量,且满足$\boldsymbol{a}\perp\boldsymbol{b}$,$\boldsymbol{c}$为$\boldsymbol{a}$,$\boldsymbol{b}$所在平面内的向量,$|\boldsymbol{c}| = 2$,则$|\boldsymbol{a} + \boldsymbol{b} - \boldsymbol{c}|$的最大值为(C)

A.4
B.$2 - \sqrt{2}$
C.$2 + \sqrt{2}$
D.$2\sqrt{2}$

答案：
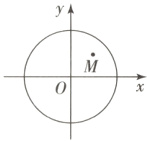
2.C[提示：因为$a,b$是两个单位向量，且$a\perp b$，所以设$a,b$分别是$x$轴与$y$轴正方向上的单位向量，则$a=(1,0)$，$b=(0,1)$，所以$a + b=(1,1)$，设$c=(x,y)$，则$a + b - c=(1 - x,1 - y)$，令$c = \overrightarrow{OC}$，
因为$|c| = 2$，所以点$C$的轨迹是以$O(0,0)$为圆心，$r = 2$为半径的圆，因为$|a + b - c|=\sqrt{(1 - x)^{2}+(1 - y)^{2}}$，所以表示点$M(1,1)$到点$C$的距离。因为$M(1,1)$到原点的距离为$|OM|=\sqrt{1^{2}+1^{2}}=\sqrt{2}$，所以$|a + b - c|_{max}=|OM| + r=\sqrt{2}+2$.

]

3. (2025·黑龙江哈尔滨师大附中高一下月考)已知$\boldsymbol{a} = (2, -1)$,$\boldsymbol{b} = (x, 2)$,且$\boldsymbol{a}//\boldsymbol{b}$,则实数$x$等于(C)

A.-1
B.1
C.-4
D.4

答案： 3.C[提示：$\because a=(2,-1),b=(x,2)$，且$a// b$，$\therefore2×2=-x$，解得$x = - 4$.]

4. (2025·黑龙江哈尔滨七十三中高一下月考)[多选]对于$\triangle ABC$,有如下判断,其中正确的是(BCD)

A.若$a = 8$,$c = 10$,$B = 60^{\circ}$,则符合条件的$\triangle ABC$有两个
B.若$\cos A = \cos B$,则$\triangle ABC$为等腰三角形
C.若$A ＞ B$,则$\sin A ＞ \sin B$
D.若$\sin^{2}A + \sin^{2}B ＜ \sin^{2}C$,则$\triangle ABC$是钝角三角形

答案： 4.BCD[提示：对于A，给出的条件为SAS（两边一夹角），符合这个条件的三角形有且只有一个，故A错误；对于B，由$\cos A=\cos B$，可得$A = B$，$\therefore\triangle ABC$为等腰三角形，故B正确；对于C，$\because A ＞ B$，$\therefore a ＞ b$，$\therefore2R\sin A ＞ 2R\sin B$，$\therefore\sin A ＞ \sin B$，故C正确；对于D，根据边角转换得$a^{2}+b^{2}-c^{2}＜0$，$\therefore C$为钝角，$\therefore\triangle ABC$是钝角三角形，故D正确.]

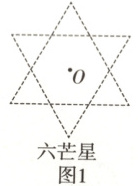
5. (2025·吉林长春十一高中高一下第一学程考试)如图1,“六芒星”是由两个边长为2的正三角形组成,中心重合于点$O$且三组对边分别平行.点$A$,$B$是“六芒星”(如图2)的两个顶点,动点$P$在“六芒星”上(内部以及边界),则$\overrightarrow{OB}·\overrightarrow{AP}$的取值范围是(A)


A.$\left[-\frac{2}{3},\frac{2}{3}\right]$
B.$\left[-\frac{3}{2},\frac{3}{2}\right]$
C.$[-\sqrt{3},\sqrt{3}]$
D.$[-2,\sqrt{3}]$

答案： 5.A[提示：以$O$为原点，$OB,OA$所在直线分别为$x$轴、$y$轴建立平面直角坐标系，如图。因为“六芒星”是由两个边长为$2$的正三角形组成，中心重合于点$O$且三组对边分别平行，所以六边形$BCDEFG$为边长为$\frac{2}{3}$的正六边形，$OA=\frac{2}{3}\sqrt{3}$，所以$OB=\frac{2}{3}$，所以$A(0,-\frac{2}{3}\sqrt{3})$，$B(\frac{2}{3},0)$，设$P(x,y)$，则$\overrightarrow{AP}=(x,y+\frac{2}{3}\sqrt{3})$，$\overrightarrow{OB}=(\frac{2}{3},0)$，所以$\overrightarrow{OB}·\overrightarrow{AP}=\frac{2}{3}x$，因为动点$P$在“六芒星”上（内部以及边界），所以$-1\leqslant x\leqslant1$，所以$-\frac{2}{3}\leqslant\frac{2}{3}x\leqslant\frac{2}{3}$，所以$-\frac{2}{3}\leqslant\overrightarrow{OB}·\overrightarrow{AP}\leqslant\frac{2}{3}$.]

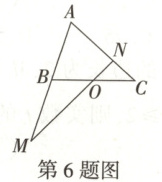
6. (2025·黑龙江大庆中学高一下月考)如图,在$\triangle ABC$中,点$O$是$BC$的中点,过点$O$的直线分别交直线$AB$,$AC$于不同的两点$M$,$N$,若$\overrightarrow{AB} = m\overrightarrow{AM}$,$\overrightarrow{AC} = n\overrightarrow{AN}$,$m ＞ 0$,$n ＞ 0$,则$\frac{2}{m} +$
$\frac{8}{n}$的最小值为(C)

A.2
B.8
C.9
D.18

答案： 6.C[提示：$\because$点$O$是$BC$的中点，$\overrightarrow{AB}=m\overrightarrow{AM}$，$\overrightarrow{AC}=n\overrightarrow{AN}$，$m＞0$，$n＞0$，$\therefore\overrightarrow{AO}=\frac{1}{2}(\overrightarrow{AB}+\overrightarrow{AC})=\frac{m}{2}\overrightarrow{AM}+\frac{n}{2}\overrightarrow{AN}$。又$M,O,N$共线，所以$m + n = 2$，且$m ＞ 0$，$n ＞ 0$，所以$\frac{2}{m}+\frac{8}{n}=(m + n)(\frac{1}{m}+\frac{4}{n})=5+\frac{n}{m}+\frac{4m}{n}\geqslant5 + 2\sqrt{\frac{n}{m}·\frac{4m}{n}}=9$，当且仅当$m=\frac{2}{3}$，$n=\frac{4}{3}$时取等号，即$\frac{2}{m}+\frac{8}{n}$的最小值为$9$.]

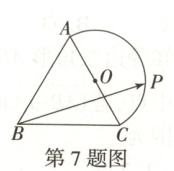
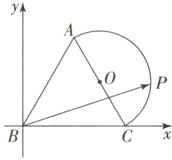
7. (2025·黑龙江哈尔滨师大附中高一下期中)[多选]如图,$\triangle ABC$为边长为2的等边三角形.以$AC$的中点$O$为圆心,1为半径作一个半圆,点$P$为此半圆弧上的一个动点,则下列说法正确的是(ACD)

A.$\overrightarrow{BO}=\frac{1}{2}\overrightarrow{BA}+\frac{1}{2}\overrightarrow{BC}$
B.$\overrightarrow{AB}·\overrightarrow{BO}=3$
C.$\overrightarrow{BP}·\overrightarrow{BC}$的最大值为5
D.若$\overrightarrow{BP}=x\overrightarrow{BA}+y\overrightarrow{BC}$,则$x + y$的最大值为$\frac{3 + \sqrt{3}}{3}$

答案：
7.ACD[提示：对于A，由题意得$\overrightarrow{BO}=\overrightarrow{BC}+\overrightarrow{CO}=\overrightarrow{BC}+\frac{1}{2}\overrightarrow{CA}=\overrightarrow{BC}+\frac{1}{2}(\overrightarrow{BA}-\overrightarrow{BC})=\frac{1}{2}\overrightarrow{BA}+\frac{1}{2}\overrightarrow{BC}$，故A正确；对于B，由A知$\overrightarrow{BO}=\frac{1}{2}\overrightarrow{BA}+\frac{1}{2}\overrightarrow{BC}$，所以$\overrightarrow{AB}·\overrightarrow{BO}=\overrightarrow{AB}·(\frac{1}{2}\overrightarrow{BA}+\frac{1}{2}\overrightarrow{BC})=-\frac{1}{2}|\overrightarrow{AB}|^{2}+\frac{1}{2}\overrightarrow{AB}·\overrightarrow{BC}=-\frac{1}{2}×4-\frac{1}{2}×2×2×\cos60^{\circ}=-2 - 1=-3$，故B错误；
对于C，以$B$为坐标原点，建立如图所示的平面直角坐标系，则$B(0,0)$，$C(2,0)$，$A(1,\sqrt{3})$，$O(\frac{3}{2},\frac{\sqrt{3}}{2})$，设$P(\frac{3}{2}+\cos\theta,\frac{\sqrt{3}}{2}+\sin\theta)$，所以$\overrightarrow{BP}·\overrightarrow{BC}=2(\frac{3}{2}+\cos\theta)=3 + 2\cos\theta$，当$\theta=0^{\circ}$时，$\overrightarrow{BP}·\overrightarrow{BC}$的最大值为$5$，故C正确；对于D，当$B,O,P$三点共线时，$|BO|=\sqrt{3}$，$|PO| = 1$，$\overrightarrow{BO}=\sqrt{3}\overrightarrow{OP}$，所以$\overrightarrow{BP}=\overrightarrow{BO}+\overrightarrow{OP}=(\sqrt{3}+1)\overrightarrow{BO}$，又$\overrightarrow{BO}=\frac{1}{2}(\overrightarrow{BA}+\overrightarrow{BC})$，所以$\overrightarrow{BP}=\frac{\sqrt{3}+1}{2}\overrightarrow{BA}+\frac{\sqrt{3}+1}{2}\overrightarrow{BC}$，所以$x = y=\frac{\sqrt{3}+1}{2}$，所以$x + y=\frac{\sqrt{3}+1}{2}+\frac{\sqrt{3}+1}{2}=\frac{3+\sqrt{3}}{3}$，故D正确。

]

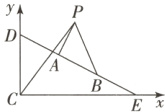
8. (2025·黑龙江哈尔滨三中月考)在$\triangle ABC$中,$|\overrightarrow{BA}+\overrightarrow{BC}| = 12$,$|\overrightarrow{AC} + \overrightarrow{AB}| = 6$,$\overrightarrow{PA}+2\overrightarrow{PC}=m\overrightarrow{AB}$,$m\in\mathbf{R}$,则$\triangle ABC$的面积的最大值为12,此时$\overrightarrow{PB}·\overrightarrow{PA}$的最小值为$\frac{39}{5}$.

答案：
8.12 $\frac{39}{5}$[提示：设点$A,B$为线段$DE$的三等分点，因为$|\overrightarrow{BA}+\overrightarrow{BC}|=|\overrightarrow{BA}+\overrightarrow{AC}-\overrightarrow{AB}|=|\overrightarrow{EA}+\overrightarrow{AC}|=|\overrightarrow{EC}|=12$，$|\overrightarrow{AC}+\overrightarrow{AB}|=|\overrightarrow{AB}+\overrightarrow{BC}+\overrightarrow{AB}|=|2\overrightarrow{AB}+\overrightarrow{BC}|=|\overrightarrow{DB}+\overrightarrow{BC}|=|\overrightarrow{DC}|=6$，所以$S_{\triangle ABC}=\frac{1}{3}S_{\triangle CDE}=\frac{1}{3}×\frac{1}{2}|\overrightarrow{CD}|×|\overrightarrow{CE}|\sin\angle DCE\leqslant\frac{1}{3}×\frac{1}{2}×12×6=12$，当且仅当$\angle DCE=90^{\circ}$时，等号成立，故$\triangle ABC$面积的最大值为$12$。因为$\angle DCE=90^{\circ}$，$|\overrightarrow{DC}|=6$，$|\overrightarrow{EC}|=12$，点$A,B$为线段$DE$的三等分点，建立如图所示的直角坐标系，所以$D(0,6)$，$E(12,0)$，$A(4,4)$，$B(8,2)$，$C(0,0)$，设$P(x,y)$，由$\overrightarrow{PA}+2\overrightarrow{PC}=m\overrightarrow{AB}$得$(4 - x,4 - y)+2(-x,-y)=(4m,-2m)$，所以$4 - 3x = 4m$，$4 - 3y=-2m$，整理得$x + 2y - 4 = 0$，所以$x=-2y + 4$，所以$\overrightarrow{PB}·\overrightarrow{PA}=(4 + 2y,2 - y)·(2y,4 - y)=(4 + 2y)(2y)+(2 - y)(4 - y)=5y^{2}+2y + 8$，即$\overrightarrow{PB}·\overrightarrow{PA}=5(y+\frac{1}{5})^{2}+\frac{39}{5}$，$m\in R$，所以$y\in R$，所以$\overrightarrow{PB}·\overrightarrow{PA}\geqslant\frac{39}{5}$，当$y=-\frac{1}{5}$时，$\overrightarrow{PB}·\overrightarrow{PA}$取得最小值，最小值为$\frac{39}{5}$。

]

9. (2025·吉林长春吉大附中实验学校高一下段考)如图,在平行四边形$ABCD$中,$\overrightarrow{BE}+\overrightarrow{CE}=\boldsymbol{0}$,$\overrightarrow{DC}=3\overrightarrow{DF}$,$DE$与$BF$相交于$O$.若$AD = 2$,$\overrightarrow{AO}·(3\overrightarrow{AD}-2\overrightarrow{AB}) = -7$,则$AB$的长为4.

答案： 9.4[提示：在平行四边形$ABCD$中，$E$是$BC$的中点，$\overrightarrow{CF}=2\overrightarrow{FD}$，$DE$与$BF$相交于$O$，设$\overrightarrow{DO}=\lambda\overrightarrow{DE}(0＜\lambda＜1)$，$\overrightarrow{BO}=\mu\overrightarrow{BF}(0＜\mu＜1)$，则$\overrightarrow{AD}+\overrightarrow{DO}=\overrightarrow{AD}+\lambda(\overrightarrow{AE}-\frac{1}{2}\overrightarrow{AD})=(1-\frac{1}{2}\lambda)\overrightarrow{AD}+\lambda\overrightarrow{AE}$，$\overrightarrow{AB}+\overrightarrow{BO}=\overrightarrow{AB}+\mu\overrightarrow{BF}=\overrightarrow{AB}+\mu(\overrightarrow{AD}-\frac{2}{3}\overrightarrow{AB})=(1-\frac{2}{3}\mu)\overrightarrow{AB}+\mu\overrightarrow{AD}$，由$\overrightarrow{AO}=\overrightarrow{AD}+\overrightarrow{DO}=\overrightarrow{AB}+\overrightarrow{BO}$，可得$\begin{cases}1-\frac{1}{2}\lambda=\mu\\1-\frac{2}{3}\mu=\lambda\end{cases}$，解得$\begin{cases}\lambda=\frac{2}{3}\\\mu=\frac{1}{4}\end{cases}$，所以$\overrightarrow{AO}=\frac{3}{4}\overrightarrow{AD}+\frac{1}{2}\overrightarrow{AB}$，所以$\overrightarrow{AO}·(\overrightarrow{AD}-2\overrightarrow{AB})=(\frac{3}{4}\overrightarrow{AD}+\frac{1}{2}\overrightarrow{AB})·(3\overrightarrow{AD}-2\overrightarrow{AB})=\frac{9}{4}|\overrightarrow{AD}|^{2}-|\overrightarrow{AB}|^{2}=-7$，又$|\overrightarrow{AD}|=2$，所以$9 - |\overrightarrow{AB}|^{2}=-7$，解得$|\overrightarrow{AB}|=4$，即$AB$的长为$4$。]

10. (2025·吉林长春东北师大附中高一下段考)已知$|\boldsymbol{a}| = 1$,$|\boldsymbol{b}| = 2$.
(1)若$\boldsymbol{a}//\boldsymbol{b}$,求$\boldsymbol{a}·\boldsymbol{b}$;
(2)若$\boldsymbol{a}$,$\boldsymbol{b}$的夹角为$60^{\circ}$,求$|\boldsymbol{a} + \boldsymbol{b}|$;
(3)若$\boldsymbol{a} - \boldsymbol{b}$与$\boldsymbol{a}$垂直,求当$k$为何值时,$(k\boldsymbol{a} - \boldsymbol{b})\perp( \boldsymbol{a} + 2\boldsymbol{b})$.

答案： 10.解：
(1)$a· b=\pm|a|·|b|=\pm2$。
(2)$a· b=|a|·|b|·\cos60^{\circ}=1$，$|a + b|^{2}=|a|^{2}+2a· b+|b|^{2}=7$，$\therefore|a + b|=\sqrt{7}$。
(3)$\because a - b$与$a$垂直，$\therefore(a - b)· a = 0$，$\therefore a· b=|a|^{2}=1$，使得$(ka - b)·(a + 2b)=0$，即$k|a|^{2}+(2k - 1)a· b - 2|b|^{2}=0$，$\therefore k = 3$。