《2025年零失误分层训练高中数学必修第二册人教版黑吉辽内蒙古专版》

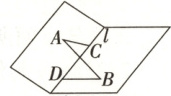
8.(2025·河北保定雄安新区高一下联考)坡度是指地表或道路等倾斜的程度,通常用垂直高度差与水平距离的比值表示.如图,这是某水渠侧面和底面的直观图,其中点$A$在该水渠的侧面上,点$B$在底面上,直线$l$是该水渠侧面与底面的交线,且$AC\perp l$,$BD\perp l$,垂足分别为$C$,$D$,若$AC=3$，$BD=5$，$CD=8$，$AB=10$，则该水渠侧面的坡度(即该水渠的侧面与底面夹角的正切值)是4$\sqrt{14}$.

答案：
8.4$\sqrt{14}$提示:如图所示，作BE//l，CE//BD，在平面BCD内，因为BD//CE，BE//CD，BD⊥CD，所以四边形BDCE为矩形，所以CE⊥l，又因为AC⊥l，所以∠ACE为该水渠侧面与底面的夹角或其补角，由题中数据可得CE = BD = 5，BE = CD = 8，因为AC⊥l，BE//l，所以AC⊥BE，因为四边形BDCE为矩形，所以BE⊥CE，因为AC，CE⊂平面ACE，AC∩CE = C，所以BE⊥平面ACE，因为AE⊂平面ACE，所以BE⊥AE，所以AE =$\sqrt{AB^{2}-BE^{2}}$=$\sqrt{10^{2}-8^{2}}$ = 6，在△ACE中，由余弦定理可得cos∠ACE =$\frac{AC^{2}+CE^{2}-AE^{2}}{2AC· CE}$=-$\frac{1}{15}$，所以sin∠ACE =$\sqrt{1-\cos^{2}\angle ACE}$=$\frac{4\sqrt{14}}{15}$，故该水渠侧面的坡度为|tan∠ACE| = |$\frac{\sin\angle ACE}{\cos\angle ACE}$| = 4$\sqrt{14}$.

9.【拓展题】已知两个平面相交,从一个平面内任选一封闭几何图形向另一个平面作投影,试证明图形的投影面积与原图形的面积之比等于两个平面所成锐二面角的余弦值.(面积投影定理)

答案：
9.证明:
(1)特殊性证明:从平面β任意选取不共线的三点A，B，C形成△ABC，向平面α作投影.由于△ABC在平面β内任意平移都不会改变其在平面α上投影的形状和大小，故△ABC向平面α作投影仅有以下两种情况:①△ABC有一边与两平面交线平行或重合，总可以通过对△ABC沿平面β平移使得其中一边与交线重合.如图所示，△ABC在平面β内，BC边在两平面交线上，A在β内，过A作平面α的垂线，垂足为A'，过A'点作A'D⊥BC于D，连接AD，A'B，A'C，则AA'⊥α，
∴AA'⊥BC，又
∵A'D⊥BC，A'D∩AA' = A'，A'D，AA'⊂平面AA'D，
∴BC⊥平面AA'D，
∴BC⊥AD，又
∵BC⊥A'D，
∴∠ADA'为α与β所成的锐二面角.在Rt△AA'D中，cos∠ADA' =$\frac{A'D}{AD}$，
∵AD⊥BC，A'D⊥BC，
∴$\frac{S_{\triangle A'BC}}{S_{\triangle ABC}}$=$\frac{\frac{1}{2}BC· A'D}{\frac{1}{2}BC· AD}$=$\frac{A'D}{AD}$ = cos∠ADA'，
∴该种情况下，命题成立.
②△ABC任意一边都不与两平面交线平行或重合.此情况下总可通过对△ABC沿平面β平移，使得其中一个顶点落在交线上，如图所示，A在平面α上，延长BC交平面α于点D，过点B作平面α的垂线交α于点B'，连接B'D，过点C作B'D的垂线交B'D于点C'，连接AD，AB'，AC'.由①中结论可知，若α与β所成的锐二面角为θ，则有$\frac{S_{\triangle A'C'D}}{S_{\triangle ACD}}$=$\frac{S_{\triangle A'B'D}}{S_{\triangle ABD}}$ = cosθ，
∴$\frac{S_{\triangle A'B'C'}}{S_{\triangle ABC}}$=$\frac{S_{\triangle A'B'D}-S_{\triangle A'C'D}}{S_{\triangle ABD}-S_{\triangle ACD}}$ = cosθ，
∴该种情况下命题仍成立.综合①②可知，在平面β内任意作三角形都有题设结论成立.
(2)一般性证明:任意封闭几何图形均可看成是由若干三角形拼接而成的，不妨设该图形由n个三角形构成，则图形总面积为各个三角形面积之和，即S = S₁+S₂+…+Sₙ，图形的投影面积也是各个三角形投影面积之和，即S' = S₁'+S₂'+...+Sₙ'.根据
(1)中特殊性证明可知，任意三角形都符合题设结论，即有$\frac{S_{1}'}{S_{1}}$=$\frac{S_{2}'}{S_{2}}$=...=$\frac{S_{n}'}{S_{n}}$ = cosθ，
∴$\frac{S'}{S}$=$\frac{S_{1}'+S_{2}'+·s+S_{n}'}{S_{1}+S_{2}+·s+S_{n}}$ = cosθ.故对任意的封闭几何图形都有题设结论成立.

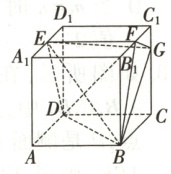
10.(2025·天津)如图，正方体$ABCD-A_{1}B_{1}C_{1}D_{1}$的棱长为4，$E$，$F$分别为$A_{1}D_{1}$，$C_{1}B_{1}$的中点，$CG=3C_{1}G$.
(1)求证$GF\perp$平面$EBF$;
(2)求平面$EBF$与平面$EBG$夹角的余弦值;
(3)求三棱锥$D-BEF$的体积.

答案：
10.解:过点F作FH⊥EB交EB于H，连接GH，AE，设平面EBF与平面EBG夹角的大小为θ，如图所示.
(1)证明:由题设条件易知GF =$\sqrt{C_{1}G^{2}+C_{1}F^{2}}$=$\sqrt{1^{2}+2^{2}}$=$\sqrt{5}$，GB =$\sqrt{CG^{2}+CB^{2}}$=$\sqrt{3^{2}+4^{2}}$ = 5，FB =$\sqrt{B_{1}B^{2}+B_{1}F^{2}}$=$\sqrt{4^{2}+2^{2}}$=2$\sqrt{5}$，
∴GF²+FB²=GB²，
∴GF⊥BF，
∵E为A₁D₁中点，F为B₁C₁中点，
∴EF//A₁B₁，又
∵A₁B₁⊥平面BB₁C₁C，
∴EF⊥平面BB₁C₁C，又
∵FG⊂平面BB₁C₁C，
∴EF⊥FG，从而可知GF⊥平面EBF.
(2)解法1(截面法):
∵EF⊥平面BB₁C₁C，且BF⊂平面BB₁C₁C，
∴EF⊥BF，
∴EB =$\sqrt{EF^{2}+BF^{2}}$=$\sqrt{4^{2}+(2\sqrt{5})^{2}}$ = 6，
∵FH⊥EB，
∴S_{△EFB}=$\frac{1}{2}$FE·FB=$\frac{1}{2}$EB·FH，
∴FH =$\frac{FE· FB}{EB}$=$\frac{4×2\sqrt{5}}{6}$=$\frac{4\sqrt{5}}{3}$，
∵GF⊥平面EBF，且FH⊂平面EBF，EB⊂平面EBF，
∴GF⊥FH，GF⊥EB，
∴EB⊥平面FGH，又
∵GH⊂平面FGH，
∴EB⊥GH，
∴∠FHG为平面EBF与平面EBG夹角的平面角，
∴cos∠FHG =$\frac{FH}{GH}$=$\frac{\frac{4\sqrt{5}}{3}}{\sqrt{(\frac{4\sqrt{5}}{3})^{2}+(\sqrt{5})^{2}}}$=$\frac{4}{5}$；解法2(面积投影定理):
∵EF⊥平面BB₁C₁C，且BF⊂平面BB₁C₁C，FG⊂平面BB₁C₁C，
∴EF⊥FB，EF⊥FG，
∴EB =$\sqrt{EF^{2}+FB^{2}}$=$\sqrt{4^{2}+(2\sqrt{5})^{2}}$ = 6，S_{△EFB}=$\frac{1}{2}$EF·FB=$\frac{1}{2}$×4×2$\sqrt{5}$=4$\sqrt{5}$，EG =$\sqrt{EF^{2}+FG^{2}}$=$\sqrt{4^{2}+(\sqrt{5})^{2}}$=$\sqrt{21}$，
∴在△EBG中，根据余弦定理可知cos∠EBG =$\frac{EB^{2}+BG^{2}-EG^{2}}{2EB· BG}$=$\frac{6^{2}+5^{2}-(\sqrt{21})^{2}}{2×6×5}$=$\frac{2}{3}$，
∴S_{△EGB}=$\frac{1}{2}$EB·BG·sin∠EBG=$\frac{1}{2}$×6×5×$\sqrt{1-(\frac{2}{3})^{2}}$=$\frac{5\sqrt{5}}{3}$，
∵GF⊥平面EBF，
∴所求余弦值为$\frac{S_{\triangle EFB}}{S_{\triangle EGB}}$=$\frac{4\sqrt{5}}{5\sqrt{5}}$=$\frac{4}{5}$.
(3)解:
∵EF//A₁B₁，A₁B₁//AB，
∴EF//AB，又
∵EF = AB = 4，且EF⊥BF，
∴四边形AEFB为矩形，
∴S_{△EFB}=S_{△EAB}，
∴V_{D - BEF}=V_{D - BEA}=$\frac{1}{3}$S_{△ABD}·A₁A=$\frac{1}{3}$×$\frac{1}{2}$×AD·AB·A₁A=$\frac{1}{6}$×4³=$\frac{32}{3}$.

11. 如图所示，正方形$ABCD$和直角梯形$BEFC$所在平面互相垂直，$BE\perp BC$，$BE// CF$，且$AB=BE=2$，$CF=3$.
(1)求证$AE//$平面$DCF$;
(2)求二面角$A-EF-C$的余弦值.

答案：
11.
(1)证明:由正方形ABCD的性质知AB//CD，又AB⊄平面DCF，CDC⊂平面DCF，
∴AB//平面DCF，
∵BE//CF，BE⊄平面DCF，CFC⊂平面DCF，
∴BE//平面DCF，
∵AB∩BE = B，AB，BE⊂平面ABE，
∴平面ABE//平面DCF，
∵AE⊂平面ABE，
∴AE//平面DCF.
(2)解法1:如图所示，延长CB交FE的延长线于G，过点B作BH⊥EG于H，连接AH.
∵正方形ABCD和直角梯形BEFC所在平面互相垂直，
∴AB⊥平面BEFC.又
∵EG⊂平面BEFC，
∴AB⊥EG，又
∵BH⊥EG，AB∩BH = B，AB，BH⊂平面ABH，
∴EG⊥平面ABH，又
∵AH⊂平面ABH，
∴EG⊥AH，
∴∠AHB是二面角A - EF - C的平面角.
∵EB//FC，
∴△GBE∽△GCF，$\frac{GB}{GC}$=$\frac{GB}{GB + AB}$=$\frac{BE}{FC}$，解得GB = 4.又
∵EB⊥BG，BH⊥EG，
∴BH =$\frac{BE· BG}{\sqrt{BE^{2}+BG^{2}}}$=$\frac{4\sqrt{5}}{5}$，
∵AB⊥平面BEFC，且BH⊂平面BEFC，
∴AB⊥BH，
∴cos∠AHB =$\frac{BH}{AH}$=$\frac{BH}{\sqrt{AB^{2}+BH^{2}}}$=$\frac{2}{3}$，
∴二面角A - EF - C的余弦值为$\frac{2}{3}$.解法2:如图所示，连接BF，AC，过点E作EG⊥CF于G.
∵正方形ABCD和直角梯形BEFC所在平面互相垂直，
∴AB⊥平面BEFC，AF⊥CB，
∴AE在平面ABCD上的投影为AB，EF =$\sqrt{FG^{2}+GE^{2}}$=$\sqrt{(FC - BE)^{2}+AB^{2}}$=$\sqrt{5}$，AF =$\sqrt{FC^{2}+AC^{2}}$=$\sqrt{FC^{2}+2AB^{2}}$=$\sqrt{17}$，又AE =$\sqrt{AB^{2}+BE^{2}}$=2$\sqrt{2}$，
∴cos∠AEF =$\frac{EF^{2}+AE^{2}-AF^{2}}{2EF· AE}$=$\frac{5 + 8 - 17}{2×\sqrt{5}×2\sqrt{2}}$=-$\frac{\sqrt{10}}{10}$，
∴sin∠AEF =$\sqrt{1 - cos^{2}\angle AEF}$=$\frac{3\sqrt{10}}{10}$，
∴S_{△AEF}=$\frac{1}{2}$EF·AE·sin∠AEF=$\frac{1}{2}$×$\sqrt{5}$×2$\sqrt{2}$×$\frac{3\sqrt{10}}{10}$ = 3.设二面角A - EF - C的平面角为θ，根据面积投影定理可知cosθ =$\frac{S_{\triangle BEF}}{S_{\triangle AEF}}$=$\frac{\frac{1}{2}BE· BC}{3}$=$\frac{2}{3}$，
∴二面角A - EF - C的余弦值为$\frac{2}{3}$.

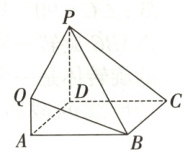
12. 在如图所示的几何体中，四边形$ABCD$是边长为2的正方形，四边形$ADPQ$是梯形，$PD// QA$，$PD\perp$平面$ABCD$，且$PD=2QA=2$.
(1)求证平面$PBC\perp$平面$QAB$;
(2)求平面$PBQ$与平面$PCD$所成角的正弦值.

答案：
12.
(1)证明:
∵PD⊥平面ABCD，PD//QA，
∴QA⊥平面ABCD，
∵BCC⊂平面ABCD，
∴QA⊥BC.又BC⊥AB，AB∩QA = A，AB，QA⊂平面QAB，
∴BC⊥平面QAB.
∵BCC⊂平面PBC，
∴平面PBC⊥平面QAB.
(2)解法1:如图所示，延长PQ交DA的延长线于点E，连接EB并延长交DC的延长线于F，连接PF，过点C作CG⊥PF于G，连接BG.则易得DE =$\sqrt{PD^{2}+PE^{2}}$=$\sqrt{PD^{2}+(2DA)^{2}}$ = 2$\sqrt{5}$，DF = 2DA = 4，
∵PD = PD，∠PDE =∠PDF = 90°，
∴Rt△PDE≌Rt△PDF，
∴PE = PF =$\sqrt{PD^{2}+DF^{2}}$ = 2$\sqrt{5}$，又
∵EB = BF =$\sqrt{2}BC$ = 2$\sqrt{2}$，
∴PB⊥EF，
∴PB =$\sqrt{PF^{2}-BF^{2}}$ = 2$\sqrt{3}$.
∵BC⊥DC，BC⊥PD，DC∩PD = D，DC，PD⊂平面PCD，
∴BC⊥平面PCD，又
∵PF⊂平面PCD，
∴BC⊥PF，又
∵CG⊥PF，BC∩CG = C，BC，CG⊂平面BCG，
∴PF⊥平面BCG，又
∵BG⊂平面BCG，
∴PF⊥BG，
∴∠BGC为平面PBQ与平面PCD所成角的平面角.
∵PB⊥EF，BG⊥PF，
∴BG =$\frac{PB· BF}{PF}$=$\frac{2\sqrt{30}}{5}$，又
∵BC⊥平面PCD，CG⊂平面PCD，
∴BC⊥CG，
∴sin∠BGC =$\frac{BC}{BG}$=$\frac{\sqrt{30}}{6}$，即平面PBQ与平面PCD所成角的正弦值为$\frac{\sqrt{30}}{6}$.解法2:如图所示，设平面PBQ与平面PCD所成角为θ，过点Q作QE⊥PD于E，连接CE，易知△PBQ在平面PCD上的投影为△PCE.
∵PD⊥平面ABCD，
∴PD⊥BC，又
∵BC⊥CD，PD∩CD = D，
∴BC⊥平面PCD，
∴BC⊥PC.
∵PQ =$\sqrt{PE^{2}+QE^{2}}$=$\sqrt{(PD - AQ)^{2}+AD^{2}}$=$\sqrt{5}$，QB =$\sqrt{AQ^{2}+AB^{2}}$=$\sqrt{5}$，PB =$\sqrt{PC^{2}+BC^{2}}$=$\sqrt{PD^{2}+DC^{2}+BC^{2}}$=2$\sqrt{3}$，
∴cos∠PQB =$\frac{PQ^{2}+BQ^{2}-PB^{2}}{2PQ· BQ}$=-$\frac{1}{5}$，
∴sin∠PQB =$\sqrt{1 - cos^{2}\angle PQB}$=$\frac{2\sqrt{6}}{5}$，
∴S_{△PQB}=$\frac{1}{2}$PQ·BQ·sin∠PQB=$\frac{1}{2}$×$\sqrt{5}$×$\sqrt{5}$×$\frac{2\sqrt{6}}{5}$=$\sqrt{6}$，
∴根据面积投影定理可知cosθ =$\frac{S_{\triangle CEP}}{S_{\triangle BQP}}$=$\frac{\frac{1}{2}(PD - AQ)· DC}{S_{\triangle BQP}}$=$\frac{\sqrt{6}}{6}$，
∴sinθ =$\sqrt{1 - cos^{2}\theta}$=$\frac{\sqrt{30}}{6}$，即平面PBQ与平面PCD所成角的正弦值为$\frac{\sqrt{30}}{6}$.


[规律方法]　二面角问题一般通过三个步骤解决:①作两个平面交线的垂面；②构建三角形，使得该三角形的两条边分别在垂面与两个平面所交的直线上，这两条边的夹角即为二面角的平面角；③通过解三角形求出二面角的平面角大小，也可以利用面积投影定理来解决.