2025年零失误分层训练高中数学必修第二册人教版黑吉辽内蒙古专版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年零失误分层训练高中数学必修第二册人教版黑吉辽内蒙古专版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第2页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
1.【题型一、二】下列命题中,真命题的个数是
⚠易错题(
①温度、速度、位移、功都是向量;
②零向量没有方向;
③向量的模一定是正数;
④直角坐标平面上的x轴、y轴都是向量.
A.0
B.1
C.2
D.3
⚠易错题(
A
)①温度、速度、位移、功都是向量;
②零向量没有方向;
③向量的模一定是正数;
④直角坐标平面上的x轴、y轴都是向量.
A.0
B.1
C.2
D.3
答案:
1.A[提示:只有速度、位移是向量,温度和功没有方向,不是向量,①错误;零向量的模为0,即向量的模不一定为正数,③错误;直角坐标平面上的$x$轴、$y$轴只有方向,没有长度,故它们不是向量,④错误.]
2.【题型一、三、四】(2025·黑龙江哈尔滨道外区高一下期中)下列说法正确的是 (
A.两个单位向量一定相等
B.若$\boldsymbol{a}$与$\boldsymbol{b}$不共线,则$\boldsymbol{a}$与$\boldsymbol{b}$都是非零向量
C.共线的单位向量必相等
D.两个相等向量的起点、方向、长度必须都相同
B
)A.两个单位向量一定相等
B.若$\boldsymbol{a}$与$\boldsymbol{b}$不共线,则$\boldsymbol{a}$与$\boldsymbol{b}$都是非零向量
C.共线的单位向量必相等
D.两个相等向量的起点、方向、长度必须都相同
答案:
2.B[提示:对于$A$,单位向量的长度一定相等,但是方向不一定相同,故$A$错误;对于$B$,若$\boldsymbol{a}$和$\boldsymbol{b}$不共线,则$\boldsymbol{a}$和$\boldsymbol{b}$都为非零向量,故$B$正确;对于$C$,共线的单位向量长度必相等,方向可能相同也可能相反,故$C$错误;对于$D$,两个相等向量的起点不一定相同,故$D$错误.]
3.【题型一、二、三、四】(2025·黑龙江哈尔滨三十二中高一下期中)[多选]下列条件能使$\boldsymbol{a} // \boldsymbol{b}$成立的是 (
A.$\boldsymbol{a} = \boldsymbol{b}$
B.$|\boldsymbol{a}| = |\boldsymbol{b}|$
C.$\boldsymbol{a}$与$\boldsymbol{b}$方向相反
D.$|\boldsymbol{a}| = 0$或$|\boldsymbol{b}| = 0$
ACD
)A.$\boldsymbol{a} = \boldsymbol{b}$
B.$|\boldsymbol{a}| = |\boldsymbol{b}|$
C.$\boldsymbol{a}$与$\boldsymbol{b}$方向相反
D.$|\boldsymbol{a}| = 0$或$|\boldsymbol{b}| = 0$
答案:
3.ACD[提示:当$\boldsymbol{a}=\boldsymbol{b}$时,向量$\boldsymbol{a},\boldsymbol{b}$方向相同,故$\boldsymbol{a}//\boldsymbol{b}$成立,$A$正确;当$\vert\boldsymbol{a}\vert=\vert\boldsymbol{b}\vert$时,向量$\boldsymbol{a},\boldsymbol{b}$的方向不确定,故$\boldsymbol{a}//\boldsymbol{b}$不一定成立,$B$错误;当$\boldsymbol{a},\boldsymbol{b}$方向相反时,$\boldsymbol{a}//\boldsymbol{b}$成立,故$C$正确;$0$与任意向量平行,故$D$正确.]
4.【题型三】如图所示,在正三角形ABC中,D,E,F均为所在边的中点,则以下向量中,与$\overrightarrow{ED}$相等的是
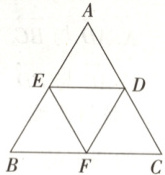
(
A.$\overrightarrow{EF}$
B.$\overrightarrow{BE}$
C.$\overrightarrow{FB}$
D.$\overrightarrow{FC}$

(
D
)A.$\overrightarrow{EF}$
B.$\overrightarrow{BE}$
C.$\overrightarrow{FB}$
D.$\overrightarrow{FC}$
答案:
4.D[提示:$\because E,D$分别是$AB,AC$的中点,$\therefore DE$是$\triangle ABC$的中位线,$\therefore DE// CB$且$DE=\frac{1}{2}CB$,又$\because F$是$BC$的中点,$\therefore$与$\overrightarrow{ED}$相等的向量有$\overrightarrow{BF},\overrightarrow{FC}$.]
5.【题型二】已知在边长为2的菱形ABCD中,$\angle ABC = 60°$,则$|\overrightarrow{BD}|$等于 (
A.1
B.$\sqrt{3}$
C.2
D.$2\sqrt{3}$
D
)A.1
B.$\sqrt{3}$
C.2
D.$2\sqrt{3}$
答案:
5.D[提示:易知$AC\perp BD$,且$\angle ABD = 30^{\circ}$,设$AC$与$BD$交于点$O$,则$AO=\frac{1}{2}AB = 1$.在$Rt\triangle ABO$中,易得$\vert\overrightarrow{BO}\vert=\sqrt{3}$,则$\vert\overrightarrow{BD}\vert = 2\vert\overrightarrow{BO}\vert = 2\sqrt{3}$.]
6.【题型二、三、四】[多选]下列说法不正确的是
⚠易错题(
A.若$|\boldsymbol{a}| = |\boldsymbol{b}|$,则$\boldsymbol{a}$,$\boldsymbol{b}$的长度相等且方向相同或相反
B.若向量$\boldsymbol{a}$,$\boldsymbol{b}$满足$|\boldsymbol{a}| > |\boldsymbol{b}|$,且方向相同,则$\boldsymbol{a} > \boldsymbol{b}$
C.若$|\boldsymbol{a}| \neq |\boldsymbol{b}|$,则$\boldsymbol{a}$与$\boldsymbol{b}$可能是共线向量
D.若非零向量$\overrightarrow{AB}$与$\overrightarrow{CD}$平行,则A,B,C,D四点共线
⚠易错题(
ABD
)A.若$|\boldsymbol{a}| = |\boldsymbol{b}|$,则$\boldsymbol{a}$,$\boldsymbol{b}$的长度相等且方向相同或相反
B.若向量$\boldsymbol{a}$,$\boldsymbol{b}$满足$|\boldsymbol{a}| > |\boldsymbol{b}|$,且方向相同,则$\boldsymbol{a} > \boldsymbol{b}$
C.若$|\boldsymbol{a}| \neq |\boldsymbol{b}|$,则$\boldsymbol{a}$与$\boldsymbol{b}$可能是共线向量
D.若非零向量$\overrightarrow{AB}$与$\overrightarrow{CD}$平行,则A,B,C,D四点共线
答案:
6.ABD[提示:对于$A$,$\vert\boldsymbol{a}\vert=\vert\boldsymbol{b}\vert$只能说明$\boldsymbol{a},\boldsymbol{b}$的长度相等,不能判断它们的方向,故$A$错误;对于$B$,向量不能比较大小,故$B$错误;对于$C$,$\vert\boldsymbol{a}\vert\neq\vert\boldsymbol{b}\vert$只能说明$\boldsymbol{a},\boldsymbol{b}$的长度不相等,它们的方向可能相同或相反,故$C$正确;对于$D$,$\overrightarrow{AB}$与$\overrightarrow{CD}$平行,$A,B,C,D$四点不一定共线,故$D$错误.]
7.【题型三、四】(原创题)如图所示,点O是正六边形ABCDEF的中心,则以图中点A,B,C,D,E,F,O中的任意一点为起点,与起点不同的另一点为终点的所有向量中,与$\overrightarrow{OA}$共线的向量有
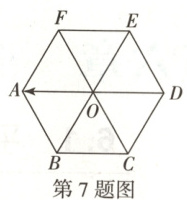
9
个,与$\overrightarrow{OA}$相等的向量有3
个.(不包含$\overrightarrow{OA}$)
答案:
7.9 3[提示:与$\overrightarrow{OA}$共线的向量有$\overrightarrow{AO},\overrightarrow{OD},\overrightarrow{DO},\overrightarrow{BC},\overrightarrow{CB},\overrightarrow{EF},\overrightarrow{FE},\overrightarrow{AD},\overrightarrow{DA}$,共9个.与$\overrightarrow{OA}$相等的向量有$\overrightarrow{EF},\overrightarrow{DO},\overrightarrow{CB}$,共3个.]
8.【题型一】(2025·四川乐山高三调研)如图,在矩形ABCD中,AB = 2BC = 2,M,N分别为边AB,CD的中点,在以A,B,C,D,M,N为起点和终点的所有有向线段表示的向量中,长度相等、方向相反的向量共有
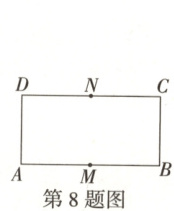
39
对.
答案:
8.39[提示:根据$\overrightarrow{AD}=\overrightarrow{MN}=\overrightarrow{BC}$,可得相等向量有3对;根据$\overrightarrow{AM}=\overrightarrow{MB}=\overrightarrow{DN}=\overrightarrow{NC}$,可得相等向量有6对;根据$\overrightarrow{AN}=\overrightarrow{MC}$,可得相等向量有1对;根据$\overrightarrow{BN}=\overrightarrow{MD}$,可得相等向量有1对;根据$\overrightarrow{AB}=\overrightarrow{DC}$,可得相等向量有1对.因此共有12对相等向量,而每对相等向量可产生两对相反向量,这样的相反向量共有24对,又每两个点产生的向量有一对相反向量,这样的相反向量共有$5 + 4 + 3 + 2 + 1 = 15$(对).综上,相反向量共有39对.]
9.【题型一】中国象棋中规定:马走“日”,象走“田”.如图所示,在中国象棋的半个棋盘(4×8的矩形中每个小方格都是单位正方形)中,若马在A处,则可跳到$A_1$处,也可跳到$A_2$处,用向量$\overrightarrow{AA_1}$,$\overrightarrow{AA_2}$表示马走了“一步”.若马在B处,则以B为起点表示马走了“一步”的向量共有
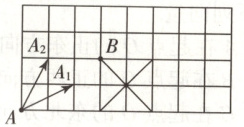
8
个.
答案:
9.8[提示:马在$B$处有8条路可走,如图所示.]

9.8[提示:马在$B$处有8条路可走,如图所示.]

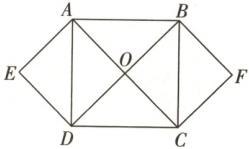
10.【题型三、四】如图所示,O为正方形ABCD的对角线的交点,四边形OAED,OCFB都是正方形.
(1)写出与$\overrightarrow{AO}$相等的向量.(不包含$\overrightarrow{AO}$)
(2)写出与$\overrightarrow{AO}$共线的向量.(不包含$\overrightarrow{AO}$)
(3)向量$\overrightarrow{AO}$与$\overrightarrow{CO}$是否相等?
(1)写出与$\overrightarrow{AO}$相等的向量.(不包含$\overrightarrow{AO}$)
(2)写出与$\overrightarrow{AO}$共线的向量.(不包含$\overrightarrow{AO}$)
(3)向量$\overrightarrow{AO}$与$\overrightarrow{CO}$是否相等?

答案:
10.解:
(1)与$\overrightarrow{AO}$相等的向量有$\overrightarrow{OC},\overrightarrow{BF},\overrightarrow{ED}$.
(2)与$\overrightarrow{AO}$共线的向量有$\overrightarrow{OA},\overrightarrow{AC},\overrightarrow{CA},\overrightarrow{BF},\overrightarrow{FB},\overrightarrow{DE},\overrightarrow{ED},\overrightarrow{OC},\overrightarrow{CO}$.
(3)$\overrightarrow{AO}$与$\overrightarrow{CO}$模相等,方向相反,所以$\overrightarrow{AO}$与$\overrightarrow{CO}$不是相等向量.
(1)与$\overrightarrow{AO}$相等的向量有$\overrightarrow{OC},\overrightarrow{BF},\overrightarrow{ED}$.
(2)与$\overrightarrow{AO}$共线的向量有$\overrightarrow{OA},\overrightarrow{AC},\overrightarrow{CA},\overrightarrow{BF},\overrightarrow{FB},\overrightarrow{DE},\overrightarrow{ED},\overrightarrow{OC},\overrightarrow{CO}$.
(3)$\overrightarrow{AO}$与$\overrightarrow{CO}$模相等,方向相反,所以$\overrightarrow{AO}$与$\overrightarrow{CO}$不是相等向量.
查看更多完整答案,请扫码查看


