2025年零失误分层训练高中数学必修第二册人教版黑吉辽内蒙古专版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年零失误分层训练高中数学必修第二册人教版黑吉辽内蒙古专版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第6页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
1. 下列说法中,正确的是 (
A.$\lambda \boldsymbol{a}$ 与 $\boldsymbol{a}$ 的方向不是相同就是相反
B.若 $\boldsymbol{a}, \boldsymbol{b}$ 共线,则存在唯一实数 $\lambda$,使 $\boldsymbol{b} = \lambda \boldsymbol{a}$
C.若 $|\boldsymbol{b}| = 2|\boldsymbol{a}|$,则 $\boldsymbol{b} = \pm 2\boldsymbol{a}$
D.若 $\boldsymbol{b} = 2\boldsymbol{a}$,则 $|\boldsymbol{b}| = 2|\boldsymbol{a}|$
D
)A.$\lambda \boldsymbol{a}$ 与 $\boldsymbol{a}$ 的方向不是相同就是相反
B.若 $\boldsymbol{a}, \boldsymbol{b}$ 共线,则存在唯一实数 $\lambda$,使 $\boldsymbol{b} = \lambda \boldsymbol{a}$
C.若 $|\boldsymbol{b}| = 2|\boldsymbol{a}|$,则 $\boldsymbol{b} = \pm 2\boldsymbol{a}$
D.若 $\boldsymbol{b} = 2\boldsymbol{a}$,则 $|\boldsymbol{b}| = 2|\boldsymbol{a}|$
答案:
1.D[提示:对于A,当$\lambda=0$时,$\lambda a=0$方向任意,故A不正确;对于B,当$a$为零向量,$b \neq 0$时,$b=\lambda a$不成立,故B不正确;对于C,$b$与$a$的方向不确定,所以$b= \pm 2a$不一定成立,故C错误;对于D,$b$与$2a$为相等向量,所以$\lvert b \rvert=2\lvert a \rvert$,故D正确.]
2. 已知实数 $m, n$ 和向量 $\boldsymbol{a}, \boldsymbol{b}$,有下列说法:
①$m(\boldsymbol{a} - \boldsymbol{b}) = m\boldsymbol{a} - m\boldsymbol{b}$;
②$(m - n)\boldsymbol{a} = m\boldsymbol{a} - n\boldsymbol{a}$;
③若 $m\boldsymbol{a} = m\boldsymbol{b}$,则 $\boldsymbol{a} = \boldsymbol{b}$;
④若 $m\boldsymbol{a} = n\boldsymbol{a} (\boldsymbol{a} \neq \boldsymbol{0})$,则 $m = n$.
其中,正确的说法是 (
A.①②③
B.①②④
C.①③④
D.②③④
①$m(\boldsymbol{a} - \boldsymbol{b}) = m\boldsymbol{a} - m\boldsymbol{b}$;
②$(m - n)\boldsymbol{a} = m\boldsymbol{a} - n\boldsymbol{a}$;
③若 $m\boldsymbol{a} = m\boldsymbol{b}$,则 $\boldsymbol{a} = \boldsymbol{b}$;
④若 $m\boldsymbol{a} = n\boldsymbol{a} (\boldsymbol{a} \neq \boldsymbol{0})$,则 $m = n$.
其中,正确的说法是 (
B
)A.①②③
B.①②④
C.①③④
D.②③④
答案:
2.B[提示:①和②属于向量数乘运算的分配律,正确;③中,当$m=0$时,$ma=mb=0$,但$a$与$b$不一定相等,故③不正确;④中,由$ma=na$得$(m - n)a = 0$.又因为$a \neq 0$,所以$m - n = 0$,即$m = n$,故④正确.]
3. (教材改编题)设向量 $\boldsymbol{a}, \boldsymbol{b}, \boldsymbol{c}$ 满足 $5(\boldsymbol{a} - 2\boldsymbol{b}) - 4(\boldsymbol{b} + 3\boldsymbol{a}) - \boldsymbol{c} = \boldsymbol{0}$,则 $\boldsymbol{c}$ 等于 (
A.$-\boldsymbol{a} + 22\boldsymbol{b}$
B.$7\boldsymbol{a} + 14\boldsymbol{b}$
C.$\boldsymbol{a} - 22\boldsymbol{b}$
D.$-7\boldsymbol{a} - 14\boldsymbol{b}$
D
)A.$-\boldsymbol{a} + 22\boldsymbol{b}$
B.$7\boldsymbol{a} + 14\boldsymbol{b}$
C.$\boldsymbol{a} - 22\boldsymbol{b}$
D.$-7\boldsymbol{a} - 14\boldsymbol{b}$
答案:
3.D[提示:$\because 5(a - 2b) - 4(b + 3a) - c = 0$,$\therefore c = - 7a - 14b$.]
4. 在 $\triangle ABC$ 中,若 $AD$ 为 $BC$ 边上的中线,点 $E$ 在 $AD$ 上,且 $AE = 2ED$,则 $\overrightarrow{EB}$ 等于 (
A.$\frac{2}{3}\overrightarrow{AB} - \frac{1}{3}\overrightarrow{AC}$
B.$\frac{2}{3}\overrightarrow{AC} - \frac{1}{3}\overrightarrow{AB}$
C.$\frac{7}{6}\overrightarrow{AB} - \frac{5}{6}\overrightarrow{AC}$
D.$\frac{7}{6}\overrightarrow{AC} - \frac{5}{6}\overrightarrow{AB}$
A
)A.$\frac{2}{3}\overrightarrow{AB} - \frac{1}{3}\overrightarrow{AC}$
B.$\frac{2}{3}\overrightarrow{AC} - \frac{1}{3}\overrightarrow{AB}$
C.$\frac{7}{6}\overrightarrow{AB} - \frac{5}{6}\overrightarrow{AC}$
D.$\frac{7}{6}\overrightarrow{AC} - \frac{5}{6}\overrightarrow{AB}$
答案:
4.A[提示:如图所示,因为$AD$为$BC$边上的中线,所以$\overrightarrow{AD}=\frac{1}{2}(\overrightarrow{AB}+\overrightarrow{AC})$,又点$E$在$AD$上,且$AE = 2ED$,所以$\overrightarrow{EA}=-\frac{2}{3}\overrightarrow{AD}$,所以$\overrightarrow{EB}=\overrightarrow{EA}+\overrightarrow{AB}=-\frac{2}{3}\overrightarrow{AD}+\overrightarrow{AB}=-\frac{2}{3} × \frac{1}{2}(\overrightarrow{AB}+\overrightarrow{AC})+\overrightarrow{AB}=-\frac{1}{3}\overrightarrow{AB}-\frac{1}{3}\overrightarrow{AC}+\overrightarrow{AB}=\frac{2}{3}\overrightarrow{AB}-\frac{1}{3}\overrightarrow{AC}$.

]
4.A[提示:如图所示,因为$AD$为$BC$边上的中线,所以$\overrightarrow{AD}=\frac{1}{2}(\overrightarrow{AB}+\overrightarrow{AC})$,又点$E$在$AD$上,且$AE = 2ED$,所以$\overrightarrow{EA}=-\frac{2}{3}\overrightarrow{AD}$,所以$\overrightarrow{EB}=\overrightarrow{EA}+\overrightarrow{AB}=-\frac{2}{3}\overrightarrow{AD}+\overrightarrow{AB}=-\frac{2}{3} × \frac{1}{2}(\overrightarrow{AB}+\overrightarrow{AC})+\overrightarrow{AB}=-\frac{1}{3}\overrightarrow{AB}-\frac{1}{3}\overrightarrow{AC}+\overrightarrow{AB}=\frac{2}{3}\overrightarrow{AB}-\frac{1}{3}\overrightarrow{AC}$.

]
5. (教材改编题)已知 $\overrightarrow{AB} = 2\boldsymbol{a} - 8\boldsymbol{b}$,$\overrightarrow{CB} = \boldsymbol{a} + 3\boldsymbol{b}$,$\overrightarrow{CD} = 2\boldsymbol{a} - \boldsymbol{b}$,则 (
A.$C, B, D$ 三点共线
B.$A, B, C$ 三点共线
C.$A, B, D$ 三点共线
D.$A, C, D$ 三点共线
C
)A.$C, B, D$ 三点共线
B.$A, B, C$ 三点共线
C.$A, B, D$ 三点共线
D.$A, C, D$ 三点共线
答案:
5.C[提示:因为$\overrightarrow{AB}=2a - 8b$,$\overrightarrow{CB}=a + 3b$,$\overrightarrow{CD}=2a - b$,所以$\overrightarrow{BC}=-a - 3b$,所以$\overrightarrow{AD}=\overrightarrow{AB}+\overrightarrow{BC}+\overrightarrow{CD}=3(a - 4b)$,$\overrightarrow{AB}=2a - 8b=2(a - 4b)$,所以$A$,$B$,$D$三点共线.]
6. (教材改编题)在 $\triangle ABC$ 中,若点 $D$ 满足 $\overrightarrow{BD} = 2\overrightarrow{DC}$,且 $\overrightarrow{AD} = m\overrightarrow{AC} + n\overrightarrow{AB}$,则 $\frac{m}{n}$ 的值为 (
A.$\frac{1}{2}$
B.$2$
C.$\frac{1}{3}$
D.$3$
B
)A.$\frac{1}{2}$
B.$2$
C.$\frac{1}{3}$
D.$3$
答案:
6.B[提示:画出图形,如图所示,所以$\overrightarrow{AD}=\overrightarrow{AB}+\overrightarrow{BD}=\overrightarrow{AB}+\frac{2}{3}\overrightarrow{BC}=\overrightarrow{AB}+\frac{2}{3}(\overrightarrow{AC}-\overrightarrow{AB})=\frac{1}{3}\overrightarrow{AB}+\frac{2}{3}\overrightarrow{AC}$,又因为$\overrightarrow{AD}=m\overrightarrow{AC}+n\overrightarrow{AB}$,所以$\begin{cases}m=\frac{2}{3}\\n=\frac{1}{3}\end{cases}$,所以$\frac{m}{n}=2$.

]
6.B[提示:画出图形,如图所示,所以$\overrightarrow{AD}=\overrightarrow{AB}+\overrightarrow{BD}=\overrightarrow{AB}+\frac{2}{3}\overrightarrow{BC}=\overrightarrow{AB}+\frac{2}{3}(\overrightarrow{AC}-\overrightarrow{AB})=\frac{1}{3}\overrightarrow{AB}+\frac{2}{3}\overrightarrow{AC}$,又因为$\overrightarrow{AD}=m\overrightarrow{AC}+n\overrightarrow{AB}$,所以$\begin{cases}m=\frac{2}{3}\\n=\frac{1}{3}\end{cases}$,所以$\frac{m}{n}=2$.

]
1.【题型一、四】已知 $P$ 是 $\triangle EFT$ 所在平面上的一点,$\overrightarrow{TF} = \lambda\overrightarrow{PE} + \overrightarrow{PF}$,$\lambda \in \mathbb{R}$,则点 $P$ 一定在 (
A.$\triangle EFT$ 内部
B.$ET$ 边所在直线上
C.$EF$ 边所在直线上
D.$FT$ 边所在直线上
B
)A.$\triangle EFT$ 内部
B.$ET$ 边所在直线上
C.$EF$ 边所在直线上
D.$FT$ 边所在直线上
答案:
1.B[提示:$\overrightarrow{TF}=\lambda\overrightarrow{PE}+\overrightarrow{PF} \Rightarrow \lambda\overrightarrow{PE}=\overrightarrow{TF}-\overrightarrow{PF}=\overrightarrow{TF}+\overrightarrow{FP}=\overrightarrow{TP}$,所以$P$,$E$,$T$三点共线,即点$P$一定在$ET$边所在直线上.]
2.【题型二、三】地砖是一种地面装饰材料,也叫地板砖,用黏土烧制而成,质坚、耐压、耐磨、防潮. 地板砖品种非常多,图案也多种多样. 如图所示的是某公司大厅的地板砖铺设方式,地板砖有正方形与正三角形两种形状,且它们的边长都相同,若 $\overrightarrow{OD} = \boldsymbol{m}$,$\overrightarrow{OI} = \boldsymbol{n}$,则 $\overrightarrow{AF}$ 等于 (
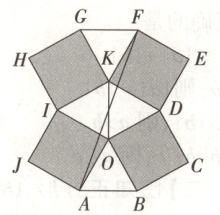
A.$(\frac{2\sqrt{3}}{3} + 1)\boldsymbol{m} + (\frac{4\sqrt{3}}{3} + 1)\boldsymbol{n}$
B.$(\frac{4\sqrt{3}}{3} + 1)\boldsymbol{m} + (\frac{2\sqrt{3}}{3} + 1)\boldsymbol{n}$
C.$(\frac{2\sqrt{3}}{3} + 1)\boldsymbol{m} + (\frac{4\sqrt{3}}{3} - 1)\boldsymbol{n}$
D.$(\frac{4\sqrt{3}}{3} + 1)\boldsymbol{m} + (\frac{2\sqrt{3}}{3} - 1)\boldsymbol{n}$
B
)
A.$(\frac{2\sqrt{3}}{3} + 1)\boldsymbol{m} + (\frac{4\sqrt{3}}{3} + 1)\boldsymbol{n}$
B.$(\frac{4\sqrt{3}}{3} + 1)\boldsymbol{m} + (\frac{2\sqrt{3}}{3} + 1)\boldsymbol{n}$
C.$(\frac{2\sqrt{3}}{3} + 1)\boldsymbol{m} + (\frac{4\sqrt{3}}{3} - 1)\boldsymbol{n}$
D.$(\frac{4\sqrt{3}}{3} + 1)\boldsymbol{m} + (\frac{2\sqrt{3}}{3} - 1)\boldsymbol{n}$
答案:
2.B[提示:如图所示,连接$OF$,$KA$,延长$AO$交$KD$于点$P$,根据对称性易知$OP \perp KD$,且$P$为$KD$的中点,则根据题意可得$\frac{AO}{OP}=\frac{2}{\sqrt{3}}$,$\therefore AO=\frac{2\sqrt{3}}{3}OP$.$\because AF=AO+OK+KF$,又由对称性易知四边形$KFOA$为平行四边形,$\therefore KF=AO$,$\therefore AF=2AO+OK=\frac{4\sqrt{3}}{3}OP+OK=\frac{4\sqrt{3}}{3} × \frac{1}{2}(OK+OD)+OK=(\frac{2\sqrt{3}}{3}+1)OK+\frac{2\sqrt{3}}{3}OD=(\frac{2\sqrt{3}}{3}+1)(OI+OD)+\frac{2\sqrt{3}}{3}OD=(\frac{4\sqrt{3}}{3}+1)m+(\frac{2\sqrt{3}}{3}+1)n$.

]
2.B[提示:如图所示,连接$OF$,$KA$,延长$AO$交$KD$于点$P$,根据对称性易知$OP \perp KD$,且$P$为$KD$的中点,则根据题意可得$\frac{AO}{OP}=\frac{2}{\sqrt{3}}$,$\therefore AO=\frac{2\sqrt{3}}{3}OP$.$\because AF=AO+OK+KF$,又由对称性易知四边形$KFOA$为平行四边形,$\therefore KF=AO$,$\therefore AF=2AO+OK=\frac{4\sqrt{3}}{3}OP+OK=\frac{4\sqrt{3}}{3} × \frac{1}{2}(OK+OD)+OK=(\frac{2\sqrt{3}}{3}+1)OK+\frac{2\sqrt{3}}{3}OD=(\frac{2\sqrt{3}}{3}+1)(OI+OD)+\frac{2\sqrt{3}}{3}OD=(\frac{4\sqrt{3}}{3}+1)m+(\frac{2\sqrt{3}}{3}+1)n$.

]
3.【题型二、三】(2025·黑龙江省实验中学高一下段考)在平行四边形 $ABCD$ 中,$E$ 是 $CD$ 边上靠近点 $C$ 的三等分点,则 $\overrightarrow{AE} + \overrightarrow{AC}$ 等于 (
A.$\frac{5}{3}\overrightarrow{AB} + 2\overrightarrow{AD}$
B.$\frac{4}{3}\overrightarrow{AB} + 2\overrightarrow{AD}$
C.$2\overrightarrow{AB} + \frac{4}{3}\overrightarrow{AD}$
D.$2\overrightarrow{AB} + \frac{5}{3}\overrightarrow{AD}$
A
)A.$\frac{5}{3}\overrightarrow{AB} + 2\overrightarrow{AD}$
B.$\frac{4}{3}\overrightarrow{AB} + 2\overrightarrow{AD}$
C.$2\overrightarrow{AB} + \frac{4}{3}\overrightarrow{AD}$
D.$2\overrightarrow{AB} + \frac{5}{3}\overrightarrow{AD}$
答案:
3.A[提示:因为$E$是$CD$边上靠近点$C$的三等分点,所以$\overrightarrow{DE}=\frac{2}{3}\overrightarrow{DC}$,在平行四边形$ABCD$中,$\overrightarrow{AE}=\overrightarrow{AD}+\overrightarrow{DE}=\overrightarrow{AD}+\frac{2}{3}\overrightarrow{DC}=\overrightarrow{AD}+\frac{2}{3}\overrightarrow{AB}$,$\overrightarrow{AC}=\overrightarrow{AB}+\overrightarrow{AD}$,所以$\overrightarrow{AE}+\overrightarrow{AC}=\frac{5}{3}\overrightarrow{AB}+2\overrightarrow{AD}$.]
4.【题型一、四】已知 $\triangle ABC$ 中,$D$ 为边 $AB$ 上一点,满足 $\overrightarrow{AB} = 2\overrightarrow{AD}$,且 $|\overrightarrow{AB}| = 2|\overrightarrow{CD}|$,则 $\triangle ABC$ 为 (
A.等腰三角形
B.等边三角形
C.直角三角形
D.等腰直角三角形
C
)A.等腰三角形
B.等边三角形
C.直角三角形
D.等腰直角三角形
答案:
4.C[提示:在$\triangle ABC$中,由$\overrightarrow{AB}=\overrightarrow{AD}+\overrightarrow{DB}=2\overrightarrow{AD}$,得$\overrightarrow{AD}=\overrightarrow{DB}$,$\therefore D$为$AB$的中点,且$\lvert \overrightarrow{AB} \rvert=2\lvert \overrightarrow{CD} \rvert$,如图所示,延长$CD$到$E$,使$\overrightarrow{DE}=\overrightarrow{CD}$,则四边形$ACBE$是平行四边形.$\because \lvert \overrightarrow{AB} \rvert=\lvert \overrightarrow{CE} \rvert$,$\therefore$平行四边形$ACBE$是矩形,即$\triangle ABC$为直角三角形.

]
4.C[提示:在$\triangle ABC$中,由$\overrightarrow{AB}=\overrightarrow{AD}+\overrightarrow{DB}=2\overrightarrow{AD}$,得$\overrightarrow{AD}=\overrightarrow{DB}$,$\therefore D$为$AB$的中点,且$\lvert \overrightarrow{AB} \rvert=2\lvert \overrightarrow{CD} \rvert$,如图所示,延长$CD$到$E$,使$\overrightarrow{DE}=\overrightarrow{CD}$,则四边形$ACBE$是平行四边形.$\because \lvert \overrightarrow{AB} \rvert=\lvert \overrightarrow{CE} \rvert$,$\therefore$平行四边形$ACBE$是矩形,即$\triangle ABC$为直角三角形.

]
查看更多完整答案,请扫码查看


