2025年零失误分层训练高中数学必修第二册人教版黑吉辽内蒙古专版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年零失误分层训练高中数学必修第二册人教版黑吉辽内蒙古专版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第30页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
1.【题型一】在$\triangle ABC$中,角$A,B,C$所对的边分别为$a,b,c$,$D$是边$AB$上一点,$CD$平分$\angle ACB$,且$CD=\sqrt{3}$,若$a\cos B+b\cos A=2c\cos C$,则$2a+b$的最小值是 (~~~)
A.$4 + 2\sqrt{2}$
B.$6$
C.$3 + 2\sqrt{2}$
D.$4$
A.$4 + 2\sqrt{2}$
B.$6$
C.$3 + 2\sqrt{2}$
D.$4$
答案:
1.C[提示:由$a\cos B+b\cos A=2c\cos C$,得$\sin A\cos B+\sin B·\cos A=2\sin C\cos C$,即$\sin(A + B)=\sin C=2\sin C\cos C$,又$\because\sin C>0$,$\therefore\cos C=\frac{1}{2}$,又$0<C<\pi$,$\therefore C=\frac{\pi}{3}$,又$CD$平分$\angle ACB$,且$CD = \sqrt{3}$,$\therefore\angle ACD=\angle BCD=\frac{\pi}{6}$,又$S_{\triangle ABC}=S_{\triangle ACD}+S_{\triangle BCD}$,则$\frac{1}{2}ab\sin\frac{\pi}{3}=\frac{1}{2}×\sqrt{3}× a\sin\frac{\pi}{6}+\frac{1}{2}×\sqrt{3}× b\sin\frac{\pi}{6}$,即$ab=a + b$,则$\frac{1}{a}+\frac{1}{b}=1$,故$2a + b=(\frac{1}{a}+\frac{1}{b})(2a + b)=3+\frac{2a}{b}+\frac{b}{a}\geqslant3 + 2\sqrt{\frac{2a}{b}×\frac{b}{a}}=3 + 2\sqrt{2}$,当且仅当$\frac{2a}{b}=\frac{b}{a}$时取等号,即$2a + b$的最小值是$3 + 2\sqrt{2}$。]
2.【题型一】设$\triangle ABC$的内角$A,B,C$所对的边分别为$a,b,c$,已知$\sin A+\sin(A+C)=2\sin C$,则 (~~~)
A.$\sin C$的最小值为$\frac{1}{2}$
B.$\sin C$的最大值为$\frac{\sqrt{3}}{2}$
C.$\cos C$的最小值为$0$
D.$\cos C$的最大值为$\frac{1}{2}$
A.$\sin C$的最小值为$\frac{1}{2}$
B.$\sin C$的最大值为$\frac{\sqrt{3}}{2}$
C.$\cos C$的最小值为$0$
D.$\cos C$的最大值为$\frac{1}{2}$
答案:
2.B[提示:由已知得$\sin A+\sin B = 2\sin C$,根据正弦定理可得$a + b = 2c$,根据余弦定理可得$\cos C=\frac{a^{2}+b^{2}-c^{2}}{2ab}=\frac{(a + b)^{2}-2ab - c^{2}}{2ab}=\frac{3c^{2}}{2ab}-1\geqslant\frac{3}{2}-1 = \frac{1}{2}$,当且仅当$a = b$时等号成立,所以$\cos C$的最小值为$\frac{1}{2}$,因为$\sin^{2}C+\cos^{2}C = 1$,所以$\sin C$的最大值为$\frac{\sqrt{3}}{2}$。]
3.【题型二】在锐角三角形$ABC$中,角$A,B,C$的对边分别为$a,b,c$,已知$a\cos B - b\cos A=b$,则$\frac{b}{a+c}$的取值范围是 (~~~)
A.$(\frac{\sqrt{3}}{3},\frac{\sqrt{2}}{2})$
B.$(2 - \sqrt{3},1)$
C.$(2 - \sqrt{3},\sqrt{2} - 1)$
D.$(\sqrt{2} + 1,\sqrt{3} + 2)$
A.$(\frac{\sqrt{3}}{3},\frac{\sqrt{2}}{2})$
B.$(2 - \sqrt{3},1)$
C.$(2 - \sqrt{3},\sqrt{2} - 1)$
D.$(\sqrt{2} + 1,\sqrt{3} + 2)$
答案:
3.C[提示:由于$a\cos B - b\cos A = b$,由正弦定理得$\sin A\cos B-\sin B\cos A=\sin(A - B)=\sin B$,故$A - B = B$,整理得$A = 2B$,由$A+B+C=\pi$,故$C=\pi - 3B$,由于$\triangle ABC$为锐角三角形,故$0<2B<\frac{\pi}{2}$,$0<\pi - 3B<\frac{\pi}{2}$,解得$\frac{\pi}{6}<B<\frac{\pi}{4}$,所以$\frac{b}{a + c}=\frac{\sin B}{\sin A+\sin C}=\frac{\sin B}{\sin 2B+\sin 3B}=\frac{\sin B}{\sin 2B+\sin 2B\cos B+\cos 2B\sin B}=\frac{1}{4\cos^{2}B + 2\cos B - 1}$,由于$\frac{\pi}{6}<B<\frac{\pi}{4}$,设$\cos B = t$,则$\frac{\sqrt{2}}{2}<t<\frac{\sqrt{3}}{2}$,所以$\frac{1}{4\cos^{2}B + 2\cos B - 1}=\frac{1}{4t^{2}+2t - 1}$,且在$t\in(\frac{\sqrt{2}}{2},\frac{\sqrt{3}}{2})$上该函数单调递减,故$\frac{b}{a + c}\in(2-\sqrt{3},\sqrt{2}-1)$。]
4.【题型三】(2025·黑龙江省实验中学高一下段考)[多选]中国南宋时期杰出数学家秦九韶在《数书九章》中提出了已知三角形三边求面积的公式,求其法是:``以小斜幂并大斜幂减中斜幂,余半之,自乘于上,以小斜幂乘大斜幂减上,余四约之,为实,一为从隅,开平方得积.''若把以上这段文字写成公式,即$S=\sqrt{\frac{1}{4}\lbrack c^{2}a^{2} - (\frac{c^{2} + a^{2} - b^{2}}{2})^{2}\rbrack}$.现有$\triangle ABC$满足$\sin A:\sin B:\sin C=\sqrt{7}:1:3$,且$S_{\triangle ABC}=\frac{3\sqrt{3}}{4}$,则 (~~~)
A.$\triangle ABC$的外接圆的半径为$\frac{\sqrt{21}}{3}$
B.若$\angle A$的平分线与$BC$交于点$D$,则$AD$的长为$\frac{3\sqrt{3}}{4}$
C.若$D$为$BC$的中点,则$AD$的长为$\frac{\sqrt{13}}{4}$
D.若$O$为$\triangle ABC$的外心,则$\overrightarrow{AO}·(\overrightarrow{AB} + \overrightarrow{AC})=5$
A.$\triangle ABC$的外接圆的半径为$\frac{\sqrt{21}}{3}$
B.若$\angle A$的平分线与$BC$交于点$D$,则$AD$的长为$\frac{3\sqrt{3}}{4}$
C.若$D$为$BC$的中点,则$AD$的长为$\frac{\sqrt{13}}{4}$
D.若$O$为$\triangle ABC$的外心,则$\overrightarrow{AO}·(\overrightarrow{AB} + \overrightarrow{AC})=5$
答案:
4.ABD[提示:对于A,根据正弦定理得$a:b:c=\sin A:\sin B:\sin C=\sqrt{7}:1:3$,设$a=\sqrt{7}m$,$b = m$,$c = 3m$,由余弦定理得$\cos A=\frac{b^{2}+c^{2}-a^{2}}{2bc}=\frac{m^{2}+9m^{2}-7m^{2}}{2· m·3m}=\frac{1}{2}$,结合$A\in(0,\pi)$,可得$A=\frac{\pi}{3}$,$\triangle ABC$的面积$S=\frac{1}{2}bc\sin A=\frac{3\sqrt{3}}{4}$,即$\frac{1}{2}· m·3m·\sin\frac{\pi}{3}=\frac{3\sqrt{3}}{4}$,解得$m = 1$,可得$a=\sqrt{7}$,所以$\triangle ABC$的外接圆的半径$R$满足$\frac{a}{\sin A}=\frac{\sqrt{7}}{\sin\frac{\pi}{3}}=2R$,解得$R=\frac{\sqrt{7}}{2\sin\frac{\pi}{3}}=\frac{\sqrt{21}}{3}$,故A正确;对于B,因为$AD$平分$\angle BAC$,$\angle BAC=\frac{\pi}{3}$,所以$\angle BAD=\angle CAD=\frac{\pi}{6}$,根据$\triangle ABC$的面积$S=\frac{1}{2}AD· AB\sin\frac{\pi}{6}+\frac{1}{2}AD· AC\sin\frac{\pi}{6}=\frac{3\sqrt{3}}{4}$,可得$\frac{3}{4}AD+\frac{1}{4}AD=\frac{3\sqrt{3}}{4}$,即$AD=\frac{3\sqrt{3}}{4}$,故B正确;对于C,若$D$为$BC$的中点,则$\overrightarrow{AD}=\frac{1}{2}(\overrightarrow{AB}+\overrightarrow{AC})$,可得$|\overrightarrow{AD}|^{2}=\frac{1}{4}(|\overrightarrow{AB}|^{2}+|\overrightarrow{AC}|^{2}+2\overrightarrow{AB}·\overrightarrow{AC})=\frac{1}{4}×(9 + 1+2×3×1×\frac{1}{2})=\frac{13}{4}$,即$|\overrightarrow{AD}|=\sqrt{\frac{13}{4}}=\frac{\sqrt{13}}{2}$,故C错误;对于D,如图,
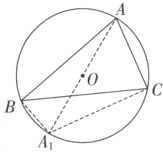
延长$AO$交外接圆于点$A_{1}$,连接$BA_{1},A_{1}C$,可知$AA_{1}$为直径,所以$A_{1}B\perp AB$,$A_{1}C\perp AC$,根据投影向量的几何意义,可得$\overrightarrow{AO}·(\overrightarrow{AB}+\overrightarrow{AC})=\frac{1}{2}(\overrightarrow{AA_{1}}·\overrightarrow{AB}+\overrightarrow{AA_{1}}·\overrightarrow{AC})=\frac{1}{2}(|\overrightarrow{AB}|^{2}+|\overrightarrow{AC}|^{2})=\frac{1}{2}×(9 +1)=5$,故D正确。]
4.ABD[提示:对于A,根据正弦定理得$a:b:c=\sin A:\sin B:\sin C=\sqrt{7}:1:3$,设$a=\sqrt{7}m$,$b = m$,$c = 3m$,由余弦定理得$\cos A=\frac{b^{2}+c^{2}-a^{2}}{2bc}=\frac{m^{2}+9m^{2}-7m^{2}}{2· m·3m}=\frac{1}{2}$,结合$A\in(0,\pi)$,可得$A=\frac{\pi}{3}$,$\triangle ABC$的面积$S=\frac{1}{2}bc\sin A=\frac{3\sqrt{3}}{4}$,即$\frac{1}{2}· m·3m·\sin\frac{\pi}{3}=\frac{3\sqrt{3}}{4}$,解得$m = 1$,可得$a=\sqrt{7}$,所以$\triangle ABC$的外接圆的半径$R$满足$\frac{a}{\sin A}=\frac{\sqrt{7}}{\sin\frac{\pi}{3}}=2R$,解得$R=\frac{\sqrt{7}}{2\sin\frac{\pi}{3}}=\frac{\sqrt{21}}{3}$,故A正确;对于B,因为$AD$平分$\angle BAC$,$\angle BAC=\frac{\pi}{3}$,所以$\angle BAD=\angle CAD=\frac{\pi}{6}$,根据$\triangle ABC$的面积$S=\frac{1}{2}AD· AB\sin\frac{\pi}{6}+\frac{1}{2}AD· AC\sin\frac{\pi}{6}=\frac{3\sqrt{3}}{4}$,可得$\frac{3}{4}AD+\frac{1}{4}AD=\frac{3\sqrt{3}}{4}$,即$AD=\frac{3\sqrt{3}}{4}$,故B正确;对于C,若$D$为$BC$的中点,则$\overrightarrow{AD}=\frac{1}{2}(\overrightarrow{AB}+\overrightarrow{AC})$,可得$|\overrightarrow{AD}|^{2}=\frac{1}{4}(|\overrightarrow{AB}|^{2}+|\overrightarrow{AC}|^{2}+2\overrightarrow{AB}·\overrightarrow{AC})=\frac{1}{4}×(9 + 1+2×3×1×\frac{1}{2})=\frac{13}{4}$,即$|\overrightarrow{AD}|=\sqrt{\frac{13}{4}}=\frac{\sqrt{13}}{2}$,故C错误;对于D,如图,

延长$AO$交外接圆于点$A_{1}$,连接$BA_{1},A_{1}C$,可知$AA_{1}$为直径,所以$A_{1}B\perp AB$,$A_{1}C\perp AC$,根据投影向量的几何意义,可得$\overrightarrow{AO}·(\overrightarrow{AB}+\overrightarrow{AC})=\frac{1}{2}(\overrightarrow{AA_{1}}·\overrightarrow{AB}+\overrightarrow{AA_{1}}·\overrightarrow{AC})=\frac{1}{2}(|\overrightarrow{AB}|^{2}+|\overrightarrow{AC}|^{2})=\frac{1}{2}×(9 +1)=5$,故D正确。]
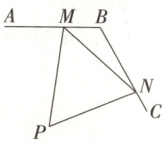
5.【题型一】(2025·黑龙江齐齐哈尔市联谊校高一下期中)如图,某幼儿园计划在一个两面靠墙的角落规划一个三角形活动区域(即$\triangle PMN$区域),地面形状如图所示. 已知点$M,N$分别在$AB,BC$上,$\angle ABC = 120^{\circ}$,$BM = 30 m$,$BN = 50 m$,$\angle MPN = 60^{\circ}$,则$PM + PN$的最大值为
140
$m$.
答案:
5.140[提示:在$\triangle BMN$中,$\angle MBN=\angle ABC = 120^{\circ}$,$BM = 30m$,$BN = 50m$,由余弦定理得$MN^{2}=BM^{2}+BN^{2}-2BM· BN·\cos120^{\circ}=4900$,所以$MN = 70m$。在$\triangle PMN$中,$\angle MPN = 60^{\circ}$,由余弦定理得$MN^{2}=PM^{2}+PN^{2}-2PM· PN·\cos60^{\circ}=(PM + PN)^{2}-3·(\frac{PM + PN}{2})^{2}$,当且仅当$PM = PN$时取等号,所以$4900\geqslant\frac{1}{4}(PM + PN)^{2}$,当且仅当$PM = PN$时等号成立,所以$PM + PN\leqslant140$,即$PM + PN$的最大值为$140m$。]
6.【题型二】如图所示,有一块三角形的空地,$\angle ABC=\frac{7\pi}{12}$,$BC=4\sqrt{2}$千米,$AB = 4$千米,则$\angle ACB =$

$\frac{\pi}{6}$
;现要在空地中修建一个三角形的绿化区域,其三个顶点为$B,D,E$,其中$D,E$为$AC$边上的点,若使$\angle DBE=\frac{\pi}{6}$,则$BD + BE$的最小值为$8(\sqrt{3}-1)$
千米.
答案:
6.$\frac{\pi}{6}$,$8(\sqrt{3}-1)$[提示:因为$\sin\angle ABC=\sin\frac{7\pi}{12}=\sin(\frac{\pi}{4}+\frac{\pi}{3})=\sin\frac{\pi}{4}\cos\frac{\pi}{3}+\cos\frac{\pi}{4}\sin\frac{\pi}{3}=\frac{\sqrt{6}+\sqrt{2}}{4}$,$\cos\angle ABC=\cos\frac{7\pi}{12}=\cos(\frac{\pi}{4}+\frac{\pi}{3})=\cos\frac{\pi}{4}\cos\frac{\pi}{3}-\sin\frac{\pi}{4}\sin\frac{\pi}{3}=\frac{\sqrt{2}-\sqrt{6}}{4}$,在$\triangle ABC$中,由余弦定理得$AC^{2}=AB^{2}+BC^{2}-2AB· BC\cos\angle ABC=8(\sqrt{3}+1)^{2}$,$\therefore AC = 2\sqrt{2}(1+\sqrt{3})$,根据正弦定理得$\frac{AC}{\sin\frac{7\pi}{12}}=\frac{AB}{\sin\angle ACB}$,解得$\sin\angle ACB=\frac{4}{2(\sqrt{2}+\sqrt{6})}=\frac{1}{2}$。因为$0<\angle ACB<\frac{\pi}{2}$,所以$\angle ACB=\frac{\pi}{6}$。设$\angle CBD=\theta$,其中$0\leqslant\theta\leqslant\frac{5\pi}{12}$,则$\angle BDC=\frac{5\pi}{6}-\theta$,$\angle BEC=\frac{2\pi}{3}-\theta$,在$\triangle BCD$中,由正弦定理得$\frac{BD}{\sin\frac{\pi}{6}}=\frac{BC}{\sin\angle BDC}$,得$BD=\frac{\sqrt{2}}{2\sin(\frac{5\pi}{6}-\theta)}$,在$\triangle BCE$中,由正弦定理得$\frac{BE}{\sin\frac{\pi}{6}}=\frac{BC}{\sin\angle BEC}$,得$BE=\frac{\sqrt{2}}{2\sin(\frac{2\pi}{3}-\theta)}$,则$BD + BE=\frac{\sqrt{2}}{2}(\frac{1}{\sin(\frac{5\pi}{6}-\theta)}+\frac{1}{\sin(\frac{2\pi}{3}-\theta)})=\frac{4\sqrt{2}(\sqrt{3}+1)(\sin\theta+\cos\theta)}{\sqrt{3}+4\sin\theta\cos\theta}$。令$t=\sin\theta+\cos\theta$,$t\in[1,\sqrt{2}]$,则$\sin\theta\cos\theta=\frac{t^{2}-1}{2}$,$BD + BE=f(t)=\frac{4\sqrt{2}(\sqrt{3}+1)t}{2t^{2}-(2-\sqrt{3})}=\frac{4\sqrt{2}(\sqrt{3}+1)}{2t-\frac{2-\sqrt{3}}{t}}$,易知分母$g(t)=2t-\frac{2-\sqrt{3}}{t}>0$,且是一个单调递增函数,则$f(t)$是一个单调递减函数,当$t=\sqrt{2}$时,$f(t)$有最小值$f(t)_{\min}=\frac{8(\sqrt{3}+1)}{2+\sqrt{3}}=8(\sqrt{3}-1)$。]
7.【题型三】已知三角形$ABC$中,内角$A,B,C$的对边分别为$a,b,c$,且$\overrightarrow{AC}·\overrightarrow{AB}=b^{2} - \frac{1}{2}ab$,$c = 2$,则$a + b$的取值范围是
$(2,4]$
.
答案:
7.$(2,4]$[提示:$\overrightarrow{AC}·\overrightarrow{AB}=|\overrightarrow{AC}|·|\overrightarrow{AB}|\cos A = bc\cos A = b^{2}-\frac{1}{2}ab$,由余弦定理得$\cos A=\frac{b^{2}+c^{2}-a^{2}}{2bc}$,所以$bc\cos A=\frac{b^{2}+c^{2}-a^{2}}{2}=b^{2}-\frac{1}{2}ab$,所以$\frac{b^{2}+c^{2}-a^{2}}{2}=b^{2}-\frac{1}{2}ab$,所以$a^{2}+b^{2}-ab = 4$,所以$4=a^{2}+b^{2}-ab=(a + b)^{2}-3ab\geqslant(a + b)^{2}-\frac{3}{4}(a + b)^{2}=\frac{1}{4}(a + b)^{2}$,当且仅当$a = b = 2$时取等号,又因为$a + b>c = 2$,所以$2<a + b\leqslant4$,所以$a + b$的取值范围是$(2,4]$。]
8.【题型三】在$\triangle ABC$中,角$A,B,C$的对边分别为$a,b,c$,点$P$是$\triangle ABC$所在平面内的动点,满足$\overrightarrow{OP}=\overrightarrow{OB}+\lambda(\frac{\overrightarrow{BC}}{\vert\overrightarrow{BC}\vert}+\frac{\overrightarrow{BA}}{\vert\overrightarrow{BA}\vert})(\lambda > 0)$.射线$BP$与边$AC$交于点$D$. 若$a^{2} + c^{2} - b^{2} = ac$,$BD = 2$,则角$B$的值为
$\frac{\pi}{3}$
,$\triangle ABC$的面积的最小值为$\frac{4\sqrt{3}}{3}$
.
答案:
8.$\frac{\pi}{3}$,$\frac{4\sqrt{3}}{3}$[提示:$\frac{\overrightarrow{BC}}{|\overrightarrow{BC}|}$表示$\overrightarrow{BC}$方向上的单位向量,$\frac{\overrightarrow{BA}}{|\overrightarrow{BA}|}$表示$\overrightarrow{BA}$方向上的单位向量,根据向量加法的几何意义可知点$P$在三角形$ABC$的角平分线上,即$BD$是三角形$ABC$的角平分线,由$a^{2}+c^{2}-b^{2}=ac$得$\cos B=\frac{a^{2}+c^{2}-b^{2}}{2ac}=\frac{1}{2}>0$,则$B$为锐角,所以$B=\frac{\pi}{3}$。依题意知$BD = 2$,根据三角形的面积公式得$\frac{1}{2}· ac·\sin\frac{\pi}{3}=\frac{1}{2}· a·2\sin\frac{\pi}{6}+\frac{1}{2}· c·2\sin\frac{\pi}{6}$,整理得$\sqrt{3}ac = 2a + 2c\geqslant2\sqrt{2a·2c}=4\sqrt{ac}$,所以$\sqrt{ac}\geqslant\frac{4}{\sqrt{3}}$,$ac\geqslant\frac{16}{3}$,当且仅当$a = c$时等号成立,所以三角形$ABC$的面积的最小值为$\frac{1}{2}×\frac{16}{3}×\sin\frac{\pi}{3}=\frac{4\sqrt{3}}{3}$。]
查看更多完整答案,请扫码查看


