《2025年零失误分层训练高中数学必修第二册人教版黑吉辽内蒙古专版》

8.【题型二、三、四】(经典 · 全国 Ⅰ ) 如图所示，在三棱锥 $A - BCD$ 中，平面 $ABD \perp$ 平面 $BCD$，$AB = AD$，$O$ 为 $BD$ 的中点.
(1) 求证 $OA \perp CD$；
(2) 若 $\triangle OCD$ 是边长为 $1$ 的等边三角形，点 $E$ 在棱 $AD$ 上，$DE = 2EA$，且二面角 $E - BC - D$ 的大小为 $45^{\circ}$，求三棱锥 $A - BCD$ 的体积.
]

答案：
8.
(1)证明:因为AB = AD，O为BD的中点，所以AO⊥BD，因为平面ABD∩平面BCD = BD，平面ABD⊥平面BCD，AO⊂平面ABD，所以AO⊥平面BCD，因为CD⊂平面BCD，所以OA⊥CD.
(2)解:如图所示，作EF⊥BD于F，作FM⊥BC于M，连接EM，因为AO⊥平面BCD，BD⊂平面BCD，所以AO⊥BD，所以AO//EF.由
(1)知AO⊥CD，所以EF⊥CD，因为BD∩CD = D，BD，CD⊂平面BCD，所以EF⊥平面BCD，因为BC⊂平面BCD，所以EF⊥BC，因为FM⊥BC，FM∩EF = F，FM，EF⊂平面EFM，所以BC⊥平面EFM，所以BC⊥ME，则∠EMF为二面角E - BC - D的平面角，即∠EMF = 45°.因为BO = OD，△OCD为正三角形，所以△BCD为直角三角形.因为DE = 2EA，易得EF = FM = $\frac{2}{3}$，所以AO = 1，因为AO⊥平面BCD，所以$V=\frac{1}{3}AO· S_{\triangle BCD}=\frac{1}{3}×1×\frac{1}{2}×1×\sqrt{3}=\frac{\sqrt{3}}{6}$.

9.【题型二、三、四】(2025 · 安徽合肥庐江高一一下期末) 如图，四棱锥 $P - ABCD$ 的底面是平行四边形，$BA = BD = 2$，$AD = 2\sqrt{2}$，$PA = PD = \sqrt{10}$，$E$，$F$ 分别是棱 $AD$，$PC$ 的中点.
(1) 求证 $EF //$ 平面 $PAB$.
(2) 若二面角 $P - AD - B$ 的平面角为 $60^{\circ}$.
①求证平面 $PBC \perp$ 平面 $ABCD$；
②求直线 $EF$ 与平面 $PBC$ 所成角的正弦值.
]

答案：
9.
(1)证明:如图，取PB的中点M，连接AM，MF，因为F为PC的中点，所以MF//BC，MF = $\frac{1}{2}$BC，由已知得BC//AD，BC = AD.又E为AD的中点，所以AE//BC，AE = $\frac{1}{2}$BC，所以MF//AE且MF = AE，所以四边形AEFM是平行四边形，所以EF//AM，又AM⊂平面PAB，EF⊄平面PAB，所以EF//平面PAB.
(2)①证明:连接PE，BE，如图，因为PA = PD，BA = BD，且E为AD的中点，所以PE⊥AD，BE⊥AD，所以∠PEB为二面角P - AD - B的平面角，即∠PEB = 60°，在△PAD中，由PA = PD = $\sqrt{10}$，AD = 2$\sqrt{2}$，得PE = 2$\sqrt{2}$，在△ABD中，由BA = BD = 2，AD = 2$\sqrt{2}$，得BE = $\sqrt{2}$，在△PBE中，∠PEB = 60°，由余弦定理得PB² = PE² + BE² - 2PE·BE$\cos\angle PEB=8 + 2-2×2\sqrt{2}×\sqrt{2}×\frac{1}{2}=6$，即PB = $\sqrt{6}$，所以PB² + BE² = PE²，即BE⊥PB，因为BC//AD，BE⊥AD，所以BE⊥BC，又BC∩PB = B，所以BE⊥平面PBC，因为BE⊂平面ABCD，所以平面PBC⊥平面ABCD.
②解:连接BF，如图，由①知BE⊥平面PBC，从而可知∠EFB为直线EF与平面PBC所成的角，因为PB = $\sqrt{6}$，AB = 2，PA = $\sqrt{10}$，所以EF = AM = $\sqrt{MB^{2}+AB^{2}}=\frac{\sqrt{22}}{2}$，在Rt△BEF中，$\sin\angle EFB=\frac{BE}{EF}=\frac{\sqrt{2}}{\frac{\sqrt{22}}{2}}=\frac{2\sqrt{11}}{11}$，故直线EF与平面PBC所成角的正弦值为$\frac{2\sqrt{11}}{11}$.

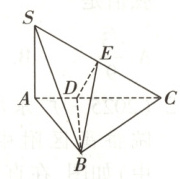
1.如图所示，在 $\triangle ABC$ 中，$AB \perp BC$，$SA \perp$ 平面 $ABC$，$DE$ 垂直平分 $SC$，分别交 $AC$，$SC$ 于 $D$，$E$ 两点，且 $SA = AB$，$SB = BC$，求二面角 $E - BD - C$ 的大小.

答案： 1.解:因为SA⊥平面ABC，所以SA⊥AC，SA⊥BD.因为E为SC的中点，SB = BC，所以BE⊥SC.又因为DE⊥SC，BE∩DE = E，BE，DE⊂平面BDE，所以SC⊥平面BDE.因为BD⊂平面BDE，所以SC⊥BD.又因为SA⊥BD，且SA∩SC = S，SA，SC⊂平面SAC，所以BD⊥平面SAC，因为DE，DC⊂平面SAC，所以BD⊥DE，BD⊥DC.所以∠EDC为所求二面角的平面角.设SA = a，则SA = AB = a，而AB⊥SA，所以SB = BC = $\sqrt{2}a$，所以SC = 2a.在Rt△SAC中，易得∠ACS = 30°，所以∠EDC = 60°，所以二面角E - BD - C的大小为60°.

2.如图所示，在长方形 $ABCD$ 中，$AB = 2$，$BC = 1$，$E$ 为 $DC$ 的中点，$F$ 为线段 $EC$(端点除外)上一动点，现将 $\triangle AFD$ 沿 $AF$ 折起，使平面 $ABD \perp$ 平面 $ABCF$. 在平面 $ABD$ 内过点 $D$ 作 $DK \perp AB$，$K$ 为垂足，设 $AK = t$，则 $t$ 的取值范围是($\frac{1}{2}$，1).
]

答案：
2.($\frac{1}{2}$，1)[提示:如图所示，过点K作KM⊥AF于点M，连接DM.
∵平面ABD⊥平面ABCF，平面ABD∩平面ABCF = AB，DK⊥AB，DK⊂平面ABD，
∴DK⊥平面ABCF，
∵AF⊂平面ABCF，
∴DK⊥AF，
∵MK⊥AF，DK∩MK = K，DK，MK⊂平面DMK，
∴AF⊥平面DMK，
∵DM⊂平面DMK，
∴AF⊥DM.观察折前的图形，可知折前的图形中D，M，K三点共线，且DK⊥AF，
∴△DAK∽△FDA，
∴$\frac{AK}{AD}=\frac{AD}{DF}$，即$\frac{t}{1}=\frac{1}{DF}$，
∴t = $\frac{1}{DF}$，
∵DF∈(1，2)，
∴t∈($\frac{1}{2}$，1).]