2025年零失误分层训练高中数学必修第二册人教版黑吉辽内蒙古专版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年零失误分层训练高中数学必修第二册人教版黑吉辽内蒙古专版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第57页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
2.【题型一】(2025·黑龙江哈尔滨道外区高一下期中) 如图, 高度为 $h$ 的圆锥形玻璃容器中装了水, 则下列四个容器中, 水的体积最接近容器容积一半的是 (

D
)
答案:
2.D[提示:方法一:设圆锥的顶点到水面的距离为$ah$,圆锥的底面半径为$r$,则水面半径为$ar$.当水的体积等于容器容积的一半时,$2×\frac{1}{3}\pi(ar)^{2}× ah=\frac{1}{3}\pi r^{2}h$,即$\frac{2}{3}× a^{3}\pi r^{2}h=\frac{1}{3}\pi r^{2}h$,解得$a^{3}=\frac{1}{2}$,因为$0.7^{3}=0.343$,$0.8^{3}=0.512$,所以$a\approx0.8$.方法二:水的体积接近容器容积的一半,则没有水的部分也是整个容器容积的一半.由于没有水的部分也是圆锥,且与整个容器相似,设没水部分的圆锥高为$x$,则根据体积比等于相似比的立方可知$(\frac{x}{h})^{3}=\frac{1}{2}$,所以$x\approx0.8h$.]
3.【题型二、三】(2025·黑龙江哈尔滨师大附中高一下期中) 在三棱雉 $P-ABC$ 中, $AB = AC = 4$, $\angle BAC = 120°$, $PA = 6$, 点 $P$ 在平面 $ABC$ 上的投影为 $A$, 则三棱雉 $P-ABC$ 的外接球的表面积为 (
A.$100\pi$
B.$75\pi$
C.$80\pi$
D.$120\pi$
A
)A.$100\pi$
B.$75\pi$
C.$80\pi$
D.$120\pi$
答案:
3.A[提示:因为点$P$在平面$ABC$上的投影为$A$,所以$PA\perp$平面$ABC$,设$\triangle ABC$的外接圆半径为$r$,因为$\angle BAC = 120^{\circ}$,$AB = AC = 4$,所以$BC^{2}=AB^{2}+AC^{2}-2AB· AC·\cos\angle BAC=48$,解得$BC = 4\sqrt{3}$,所以$2r=\frac{BC}{\sin120^{\circ}}$,所以$r = 4$,设三棱锥$P - ABC$的外接球的半径为$R$,则$(2r)^{2}+PA^{2}=(2R)^{2}$,即$64 + 36=4R^{2}$,所以$4R^{2}=100$,所以三棱锥$P - ABC$的外接球的表面积是$4\pi R^{2}=100\pi$.]
4.【题型二、三】已知正三棱雉 $A-BCD$, 各棱长均为 $\sqrt{3}$, 则其外接球的体积为 (
A.$\frac{9\sqrt{3}}{8}\pi$
B.$\frac{81\sqrt{2}}{16}\pi$
C.$\frac{9\sqrt{2}}{8}\pi$
D.$\frac{9\sqrt{3}}{16}\pi$
C
)A.$\frac{9\sqrt{3}}{8}\pi$
B.$\frac{81\sqrt{2}}{16}\pi$
C.$\frac{9\sqrt{2}}{8}\pi$
D.$\frac{9\sqrt{3}}{16}\pi$
答案:
4.C[提示:由$A - BCD$是正三棱锥,底面是正三角形,边长为$\sqrt{3}$,则高线的投影在底面正三角形的重心处,则外接球的球心在高线上,且到各个顶点的距离相等.如图,取$CD$的中点$F$,连接$BF$,过$A$作$AE\perp BF$,垂足为$E$,则$BE = 2EF$,由$AB = BC = CD = AD = BD=\sqrt{3}$,则在$Rt\triangle BCF$中,有$BF=\sqrt{(\sqrt{3})^{2}-(\frac{\sqrt{3}}{2})^{2}}=\frac{3}{2}$,所以$BE=\frac{2}{3}×\frac{3}{2}=1$.在$Rt\triangle ABE$中,有$AE=\sqrt{(\sqrt{3})^{2}-1^{2}}=\sqrt{2}$.设外接球的半径为$r$,则$BE^{2}+(AE - r)^{2}=r^{2}$,即$1^{2}+(\sqrt{2}-r)^{2}=r^{2}$,解得$r=\frac{3\sqrt{2}}{4}$,故外接球的体积为$V=\frac{4}{3}\pi r^{3}=\frac{4}{3}\pi×(\frac{3\sqrt{2}}{4})^{3}=\frac{9\sqrt{2}}{8}\pi$.]
4.C[提示:由$A - BCD$是正三棱锥,底面是正三角形,边长为$\sqrt{3}$,则高线的投影在底面正三角形的重心处,则外接球的球心在高线上,且到各个顶点的距离相等.如图,取$CD$的中点$F$,连接$BF$,过$A$作$AE\perp BF$,垂足为$E$,则$BE = 2EF$,由$AB = BC = CD = AD = BD=\sqrt{3}$,则在$Rt\triangle BCF$中,有$BF=\sqrt{(\sqrt{3})^{2}-(\frac{\sqrt{3}}{2})^{2}}=\frac{3}{2}$,所以$BE=\frac{2}{3}×\frac{3}{2}=1$.在$Rt\triangle ABE$中,有$AE=\sqrt{(\sqrt{3})^{2}-1^{2}}=\sqrt{2}$.设外接球的半径为$r$,则$BE^{2}+(AE - r)^{2}=r^{2}$,即$1^{2}+(\sqrt{2}-r)^{2}=r^{2}$,解得$r=\frac{3\sqrt{2}}{4}$,故外接球的体积为$V=\frac{4}{3}\pi r^{3}=\frac{4}{3}\pi×(\frac{3\sqrt{2}}{4})^{3}=\frac{9\sqrt{2}}{8}\pi$.]

5.【题型一、二、三】(2025·黑龙江哈尔滨松雷中学高一下期中) [多选] 如图, $AC$ 为圆锥 $SO$ 底面圆 $O$ 的直径, 点 $B$ 是圆 $O$ 上异于 $A, C$ 的动点, $SO = OC = \sqrt{3}$, 则下列结论正确的是 (
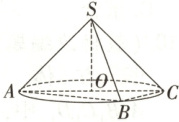
A.圆锥 $SO$ 的侧面积为 $3\pi$
B.三棱雉 $S-ABC$ 体积的最大值为 $\sqrt{3}$
C.圆锥 $SO$ 的外接球体积为 $4\sqrt{3}\pi$
D.若 $AB = BC$, $E$ 为线段 $AB$ 上的动点, 则 $SE + CE$ 的最小值为 $3 + \sqrt{3}$
BCD
)
A.圆锥 $SO$ 的侧面积为 $3\pi$
B.三棱雉 $S-ABC$ 体积的最大值为 $\sqrt{3}$
C.圆锥 $SO$ 的外接球体积为 $4\sqrt{3}\pi$
D.若 $AB = BC$, $E$ 为线段 $AB$ 上的动点, 则 $SE + CE$ 的最小值为 $3 + \sqrt{3}$
答案:
5.BCD[提示:在$Rt\triangle SOC$中,$SC=\sqrt{SO^{2}+OC^{2}}=\sqrt{6}$,$\therefore$圆锥的母线长$l=\sqrt{6}$,半径$r = OC=\sqrt{3}$.对于A,圆锥的侧面积为$\pi rl=3\sqrt{2}\pi$,故A不正确;对于B,当$OB\perp AC$时,$\triangle ABC$的面积最大,此时$S_{\triangle ABC}=\frac{1}{2}×2\sqrt{3}×\sqrt{3}=3$,$\therefore$三棱锥$S - ABC$体积的最大值为$\frac{1}{3}S_{\triangle ABC}· SO=\frac{1}{3}×3×\sqrt{3}=\sqrt{3}$,故B正确;对于C,如图,设外接球球心为$O'$,半径为$R$,则$AO'^{2}=O'O^{2}+AO^{2}$,即$R^{2}=(\sqrt{3}-R)^{2}+(\sqrt{3})^{2}$,$\therefore R=\sqrt{3}$,$\therefore$圆锥$SO$的外接球体积为$\frac{4}{3}\pi×(\sqrt{3})^{3}=4\sqrt{3}\pi$,故C正确;对于D,由$AB = BC$,$\angle ABC = 90^{\circ}$,$AC = 2\sqrt{3}$,得$AB = BC=\sqrt{6}$,又$SA = SB=\sqrt{6}$,$\therefore\triangle SAB$为等边三角形,$\angle SBA = 60^{\circ}$,将$\triangle SAB$以$AB$为轴旋转到与$\triangle ABC$共面,得到$\triangle SAB'$,此时$(SE + CE)_{\min}=SC$,$\because SB = BC=\sqrt{6}$,$\angle SBC=\angle SBA+\angle ABC=150^{\circ}$,$\therefore SC^{2}=SB^{2}+BC^{2}-2× SB× BC×\cos150^{\circ}=12 + 6\sqrt{3}$,$\therefore(SE + CE)_{\min}=SC=\sqrt{3}+3$,故D正确.]
5.BCD[提示:在$Rt\triangle SOC$中,$SC=\sqrt{SO^{2}+OC^{2}}=\sqrt{6}$,$\therefore$圆锥的母线长$l=\sqrt{6}$,半径$r = OC=\sqrt{3}$.对于A,圆锥的侧面积为$\pi rl=3\sqrt{2}\pi$,故A不正确;对于B,当$OB\perp AC$时,$\triangle ABC$的面积最大,此时$S_{\triangle ABC}=\frac{1}{2}×2\sqrt{3}×\sqrt{3}=3$,$\therefore$三棱锥$S - ABC$体积的最大值为$\frac{1}{3}S_{\triangle ABC}· SO=\frac{1}{3}×3×\sqrt{3}=\sqrt{3}$,故B正确;对于C,如图,设外接球球心为$O'$,半径为$R$,则$AO'^{2}=O'O^{2}+AO^{2}$,即$R^{2}=(\sqrt{3}-R)^{2}+(\sqrt{3})^{2}$,$\therefore R=\sqrt{3}$,$\therefore$圆锥$SO$的外接球体积为$\frac{4}{3}\pi×(\sqrt{3})^{3}=4\sqrt{3}\pi$,故C正确;对于D,由$AB = BC$,$\angle ABC = 90^{\circ}$,$AC = 2\sqrt{3}$,得$AB = BC=\sqrt{6}$,又$SA = SB=\sqrt{6}$,$\therefore\triangle SAB$为等边三角形,$\angle SBA = 60^{\circ}$,将$\triangle SAB$以$AB$为轴旋转到与$\triangle ABC$共面,得到$\triangle SAB'$,此时$(SE + CE)_{\min}=SC$,$\because SB = BC=\sqrt{6}$,$\angle SBC=\angle SBA+\angle ABC=150^{\circ}$,$\therefore SC^{2}=SB^{2}+BC^{2}-2× SB× BC×\cos150^{\circ}=12 + 6\sqrt{3}$,$\therefore(SE + CE)_{\min}=SC=\sqrt{3}+3$,故D正确.]

6.【题型一、二、三】如图, 在水平放置的直径与高相等的圆柱内, 放入两个半径相等的小球 (球 $A$ 和球 $B$), 圆柱的底面直径为 $2 + \sqrt{2}$, 向圆柱内注满水, 水面刚好淹没小球 $B$.
(1) 求球 $A$ 的体积;
(2) 求圆柱的侧面积与球 $B$ 的表面积之比.

(1) 求球 $A$ 的体积;
(2) 求圆柱的侧面积与球 $B$ 的表面积之比.

答案:
6.解:
(1)设圆柱的底面半径为$R$,小球的半径为$r$,且$r<R$,连接$AB$,由圆柱与球的性质知$AB^{2}=(2r)^{2}=(2R - 2r)^{2}+(2R - 2r)^{2}$,即$r^{2}-4Rr + 2R^{2}=0$,$\because r<R$,$\therefore r=(2 - \sqrt{2})× R=(2 - \sqrt{2})×\frac{2+\sqrt{2}}{2}=1$.$\therefore$球$A$的体积为$V=\frac{4}{3}\pi r^{3}=\frac{4}{3}\pi$.
(2)球$B$的表面积为$S_{1}=4\pi r^{2}=4\pi$,圆柱的侧面积为$S_{2}=2\pi R·2R=4\pi R^{2}=(6 + 4\sqrt{2})\pi$,$\therefore$圆柱的侧面积与球$B$的表面积之比为$\frac{3 + 2\sqrt{2}}{2}$.
(1)设圆柱的底面半径为$R$,小球的半径为$r$,且$r<R$,连接$AB$,由圆柱与球的性质知$AB^{2}=(2r)^{2}=(2R - 2r)^{2}+(2R - 2r)^{2}$,即$r^{2}-4Rr + 2R^{2}=0$,$\because r<R$,$\therefore r=(2 - \sqrt{2})× R=(2 - \sqrt{2})×\frac{2+\sqrt{2}}{2}=1$.$\therefore$球$A$的体积为$V=\frac{4}{3}\pi r^{3}=\frac{4}{3}\pi$.
(2)球$B$的表面积为$S_{1}=4\pi r^{2}=4\pi$,圆柱的侧面积为$S_{2}=2\pi R·2R=4\pi R^{2}=(6 + 4\sqrt{2})\pi$,$\therefore$圆柱的侧面积与球$B$的表面积之比为$\frac{3 + 2\sqrt{2}}{2}$.
7.【题型一、二、四】在两块钢板上打孔, 用钉帽呈半球形、钉身为圆柱形的铆钉 (如图(1)) 穿在一起, 在没有帽的一端锤打出一个帽, 使得与钉帽的大小相等, 铆合的两块钢板成为某种钢结构的配件, 其截面图如图(2). (单位: mm, 加工中不计损失)
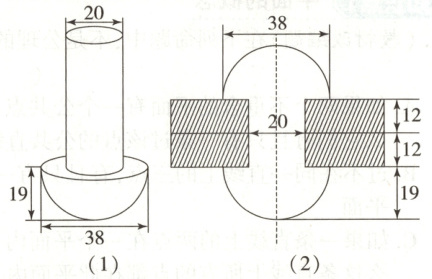
(1) 若钉身长度是钉帽高度的2倍, 求铆钉的表面积;
(2) 若每块钢板的厚度为12 mm, 求钉身的长度 (结果精确到1 mm).

(1) 若钉身长度是钉帽高度的2倍, 求铆钉的表面积;
(2) 若每块钢板的厚度为12 mm, 求钉身的长度 (结果精确到1 mm).
答案:
7.解:
(1)设钉身的长度为$h$,钉身的底面半径为$r$,钉帽的半径为$R$,由题意可知圆柱的高$h = 2R = 38$,底面半径$r = 10$,圆柱的侧面积$S_{1}=2\pi r· h=760\pi$,半球的表面积$S_{2}=\frac{1}{2}×4\pi R^{2}+\pi R^{2}=1083\pi$,所以铆钉的表面积$S = S_{1}+S_{2}=760\pi+1083\pi=1843\pi(mm^{2})$.
(2)设铆合后的钉身的长度为$h_{1}$,则铆合后钉身的体积$V_{1}=\pi r^{2}· h_{1}=100×24×\pi=2400\pi$,一个钉帽的体积$V_{2}=\frac{1}{2}×\frac{4}{3}\pi× R^{3}=\frac{2}{3}×19^{3}×\pi=\frac{13718\pi}{3}$.设钉身长度为$l$,则铆合前钉身的体积$V_{3}=\pi r^{2}· l=100\pi l$,由于$V_{3}=V_{1}+V_{2}$,所以$2400\pi+\frac{13718\pi}{3}=100\pi l$,解得$l\approx70mm$.即钉身的长度约为$70mm$.
(1)设钉身的长度为$h$,钉身的底面半径为$r$,钉帽的半径为$R$,由题意可知圆柱的高$h = 2R = 38$,底面半径$r = 10$,圆柱的侧面积$S_{1}=2\pi r· h=760\pi$,半球的表面积$S_{2}=\frac{1}{2}×4\pi R^{2}+\pi R^{2}=1083\pi$,所以铆钉的表面积$S = S_{1}+S_{2}=760\pi+1083\pi=1843\pi(mm^{2})$.
(2)设铆合后的钉身的长度为$h_{1}$,则铆合后钉身的体积$V_{1}=\pi r^{2}· h_{1}=100×24×\pi=2400\pi$,一个钉帽的体积$V_{2}=\frac{1}{2}×\frac{4}{3}\pi× R^{3}=\frac{2}{3}×19^{3}×\pi=\frac{13718\pi}{3}$.设钉身长度为$l$,则铆合前钉身的体积$V_{3}=\pi r^{2}· l=100\pi l$,由于$V_{3}=V_{1}+V_{2}$,所以$2400\pi+\frac{13718\pi}{3}=100\pi l$,解得$l\approx70mm$.即钉身的长度约为$70mm$.
1. 一飞行昆虫被长为12 cm的细绳绑在房间一角, 则飞虫活动范围的体积的最大值为
(
A.$144\pi$ cm³
B.$288\pi$ cm³
C.$576\pi$ cm³
D.$864\pi$ cm³
(
B
)A.$144\pi$ cm³
B.$288\pi$ cm³
C.$576\pi$ cm³
D.$864\pi$ cm³
答案:
1.B[提示:飞虫活动的范围是以墙角顶点为球心,半径为$12cm$的球在房间内的部分,即整个球的$\frac{1}{8}$,故飞虫活动范围的体积为$\frac{1}{8}×\frac{4}{3}\pi×12^{3}=288\pi(cm^{3})$.]
2. 已知一个圆锥的底面半径为6, 其体积为 $96\pi$, 则该圆锥的侧面积为
60π
, 圆锥内半径最大的球的体积为36π
.
答案:
2.$60\pi\ 36\pi$[提示:设圆锥的高为$h$,因为圆锥的底面半径为$6$,其体积为$96\pi$,所以$V=\frac{1}{3}\pi·6^{2}· h=96\pi$,解得$h = 8$,则圆锥的母线长为$l=\sqrt{h^{2}+r^{2}}=\sqrt{8^{2}+6^{2}} = 10$,所以圆锥的侧面积为$S=\pi rl=60\pi$.如图,球为圆锥的内切球时,球的半径最大,由图知$\frac{h - R}{l}=\frac{R}{r}$,解得$R = 3$,所以圆锥内半径最大的球的体积是$V'=\frac{4}{3}\pi R^{3}=36\pi$.]
2.$60\pi\ 36\pi$[提示:设圆锥的高为$h$,因为圆锥的底面半径为$6$,其体积为$96\pi$,所以$V=\frac{1}{3}\pi·6^{2}· h=96\pi$,解得$h = 8$,则圆锥的母线长为$l=\sqrt{h^{2}+r^{2}}=\sqrt{8^{2}+6^{2}} = 10$,所以圆锥的侧面积为$S=\pi rl=60\pi$.如图,球为圆锥的内切球时,球的半径最大,由图知$\frac{h - R}{l}=\frac{R}{r}$,解得$R = 3$,所以圆锥内半径最大的球的体积是$V'=\frac{4}{3}\pi R^{3}=36\pi$.]

查看更多完整答案,请扫码查看


